ПОЛУНЕПРЕРЫВНАЯ ФУНКЦИЯ

ПОЛУНЕПРЕРЫВНАЯ ФУНКЦИЯ

функция из первого Бэра класса. Подробнее, числовая функция f, определенная на полном метрич. пространстве X, наз. полунепрерывной снизу (сверху) в точке , если


Функция f наз. полунепрерывной снизу (сверху) на X, если она. полунепрерывна снизу (сверху) для всех 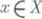. Предел монотонно возрастающей (убывающей) последовательности полунепрерывных снизу (сверху) в точке x0 функций есть П. ф. снизу (сверху) в х 0. Если и(х).и v(x).есть П. ф. соответственно снизу и сверху на Xи для всех имеет место 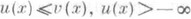, v(x)<+, то существует непрерывная на Xфункция f такая, что 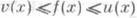для всех 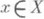. Если m - неотрицательная мера на , то для любой m-измеримой функции 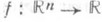существуют две последовательности функций {un(x)} и {vn(x)}, удовлетворяющие условиям:

1) un(x) полунепрерывны снизу, vn (х).полунепрерывны сверху,

2) каждая функция и п (х). ограничена снизу, каждая функция vn(x).- сверху,

3) последовательность {и n} невозрастающая, последовательность {vn} неубывающая,

4) для всех химеет место неравенство

5) m-почти всюду.


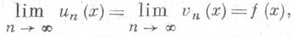
6) если для функция f суммируема, , то и

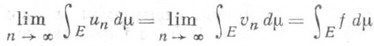
(теорема Витали - Каратеодори).

Лит.:[1] Натансон И. П., Теория функций вещественной переменной, 3 изд., М., 1974; [2] Сакс С., Теория интеграла, пер. с англ., М., 1949. И. А. Виноградова.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Нужно сделать НИР?

Полезное


Смотреть что такое "ПОЛУНЕПРЕРЫВНАЯ ФУНКЦИЯ" в других словарях:

  • Полунепрерывная функция — полунепрерывная сверху функция. полунепрерывная снизу функция. Полунепрерывность в математическом анализе это свойство функции более слабое, чем непрерывность. Функция полунепрерывна сверху в точке, если зн …   Википедия

  • полунепрерывная функция — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN semi continuous function …   Справочник технического переводчика

  • Полунепрерывная функция —         понятие математического анализа. П. ф. снизу (сверху) в точке х0 называется функция, для которой f (x) = f (x0) [соответственно f (x) = f (x0)]. Иначе, функция полунепрерывна снизу в точке x0, если для всякого ε > 0 найдётся такое δ > 0,… …   Большая советская энциклопедия

  • ПЛЮРИСУБГАРМОНИЧЕСКАЯ ФУНКЦИЯ — действительная функция u=u(z), , п комплексных переменных z=(zl,. . ., zn).в области Dкомплексного пространства , удовлетворяющая следующим условиям: 1) и(z) полунепрерывна сверху всюду в D;2) u(z0+la). есть субгармоническая функция переменного в …   Математическая энциклопедия

  • ГАРМОНИЧЕСКОЕ ПРОСТРАНСТВО — топология, пространство X с пучком непрерывных действительных функций с аксиоматически фиксируемыми в той или иной форме тремя основными свойствами классических гармонических функций:свойство сходимости, выражаемое второй Гарнака теоремой;принцип …   Математическая энциклопедия

  • РИССА ПОТЕНЦИАЛ — a потенциал, потенциал вида где m положительная борелевская мера с компактным носителем на евклидовом пространстве расстояние между точками . При и a=n 2 Р. п. совпадает с классическим ньютоновым потенциалом;при n=2 и предельным случаем Р. п. в… …   Математическая энциклопедия

  • СПЕКТРАЛЬНЫЙ РАДИУС — элемента банаховой алгебры радиус наименьшего круга на плоскости, содержащего спектр этого элемента. С. р. элемента асвязан с нормами его степеней формулой из к рой следует, в частности, что С. р. ограниченного оператора в банаховом пространстве… …   Математическая энциклопедия

  • ШТРАФНЫХ ФУНКЦИЙ МЕТОД — метод сведения условно экстремальных задач к задачам безусловной оптимизации. Проиллюстрировать Ш. ф. м. можно на примере задач математического программирования. Рассматривается задача минимизации функции на множестве из п мер ного евклидова… …   Математическая энциклопедия

  • БЭРА ТЕОРЕМА — 1) Б. т. о полных пространствах: любая счетная система открытых и всюду плотных в данном полном метрическом пространстве множеств имеет непустое, п даже всюду плотное в этом пространстве пересечение. Эквивалентная формулировка: полное метрич.… …   Математическая энциклопедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»