ДЗЕТА-ФУНКЦИЯ

z-ф у нкция, - 1) Д.-ф. в теории чисел - класс аналитич. функций комплексного переменного, состоящий из z-функции Римана, ее обобщений и аналогов. Д.-ф. и их обобщения в виде L-функций (см. Дирихле L-функции )лежат в основе современной аналитич. теории чисел. Кроме z-функции Римана выделяются обебщенная Д.-ф. z(s, a), дзета-функция Дедекинда, конгруэнц Д.-ф. и др.

Дзета-функция Римана определяется рядом Дирихле

абсолютно и равномерно сходящимся в любой конечной области комплексной s-плоскости, для к-рой d>0. При s>1 справедливо представление в виде произведения Эйлера

где рпробегает все простые числа.

Тождественность ряда (1) и произведения (2) представляет собой одно из основных свойств функции z(s). Оно позволяет получить многочисленные соотношения, связывающие z(s)с важнейшими теоретико-числовыми функциями. Так, при s>1

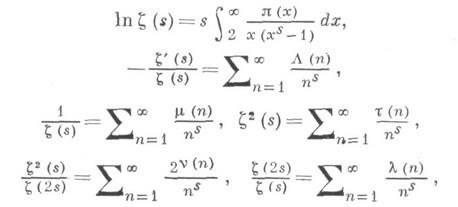
где (х)- число простых чисел - Мангольдта функция,m(n).- Мёбиуса функция,t(п) - число делителей числа га, v(n) - число простых делителей числа п,l(n) - Лиувилля функция. Отсюда та исключительная роль, к-рую играет z(s) в теории чисел. Как функция действительного переменного, z(s). была введена в 1737 Л. Эйлером (L. Euler, см. [1]), к-рый указал и ее разложение в произведение (2). Затем эта функция рассматривалась П. Дирихле (P. Dirichlet) и, особенно успешно, П. Л. Чебышевым (см. [2]) в связи с изучением закона распределения простых чисел. Однако наиболее глубокие свойства функции z(s). были обнаружены позднее, когда ее стали рассматривать как функцию комплексного переменного. Первым это сделал в 1876 Б. Риман (В. Riemann, см. [3]), к-рый показал следующее.

а) z(s) допускает аналитич. родолжение на всю комплексную s-плоскость в виде

где Г(w) - гамма-функция,

б) z(s) является регулярной функцией для всех значений s, кроме s=l, где она имеет простой полюс с вычетом, равным 1, и удовлетворяет функциональному уравнению

Это уравнение наз. функциональным уравнением Римана. Для функции

введенной Б. Риманом для исследования Д.-ф. и называемой кси-функцией Риман а, это уравнение принимает вид

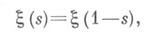
а если положить

то оно принимает вид

Последняя функция .3 замечательна тем, что она является четной целой функцией, действительной для действительных t, и ее нули на действительной оси соответствуют нулям функции z(s) на прямой 0=1/2.

в) Поскольку для s>1, то в силу (4) в полуплоскости s>0 эта функция имеет лишь простые нули в точках s=2v, v=l, 2,. .. Эти нули наз. тривиальными нулями Д.-ф. z(s). Далее z(s) неравно 0 для 0<s<1. Таким образом, все нетривиальные нули Д.-ф. z(s). являются комплексными числами, обладают свойством симметрии относительно действительной оси i=0 и относительно вертикали s=1/2 и лежат в полосе 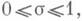к-рая наз. критической полосой.

продолжение Дзета-функция...

Б. Риман высказал также следующие гипотезы.

1.Число N(T)нулей функции z(s). в прямоугольнике 0<i<T выражается формулой

2.Пусть р пробегает нетривиальные нули z(s). Тогда ряд сходится, а ряд расходится.

3. Функция z(s) представима в виде

4. Пусть

Тогда при

где Их- интегральный логарифм,

5. Все нетривиальные нули Д.-ф. z(s) лежат на прямой

После Б. Римана проблема значений и, в частности, нулей Д.-ф. приобрела широкую известность и ей посвящено большое число исследований. Гипотезы Римана 2 и 3 были доказаны Ж. Адамаром (J. Hadamard, 1893), причем оказалось, что в гипотезе 3 a=1/2, b = ln2+ +lnp-1-, где С- Эйлера постоянная;гипотезы 1 и 4 доказаны X. Мангольдтом (Н. Mangoldt, 1894), к-рый, кроме того, получил, для простых чисел, следующий важный аналог формулы 5. Если

то при

где r=b+ig пробегает нетривиальные нули z(s), a символ означает предел суммы при T стремящимся к бесконечности. Эта формула, как и формула (5), показывает, что проблема распределения простых чисел в натуральном ряду тесно связана с расположением нетривиальных нулей функции z(s).

Последняя гипотеза 5 не доказана и не опровергнута. Это - знаменитая Римана гипотеза о нулях Д.-Ф.

Функция z(s)однозначно определяется своим функциональным уравнением. Точнее (см. [4]), любая функция, представимая обыкновенным рядом Дирихле и удовлетворяющая уравнению (4), при довольно широких условиях относительно ее регулярности, совпадает с z(s) с точностью до постоянного множителя.

При и постоянном h>0 для 0<s<1, x>h, y>h, 2pxy=|t| имеет место приближенное функциональное уравнение

полученное X. Харди (Н. Hardy) и Дж. Литлвудом (J. Littlewood) в 1920 (см. [4]). Это уравнение играет значительную роль в современной теории Д.-ф. и ее приложениях. Существуют общие методы получения такого рода результатов не только для класса Д.-ф., но и вообще функций Дирихле, обладающих функциональным уравнением риманова типа (3). Наиболее совершенный из них указан в [5]; в случае z(s)он приводит, при любом t с |argt|<p/2, к соотношению

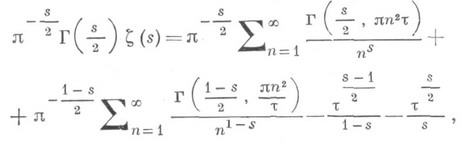
где F(z, x)- неполная гамма-функция;при

получается приближенное уравнение (6); при t=1 это соотношение совпадает с исходной формулой (3).

Главной проблемой в теории Д.-ф. является проблема расположения ее нетривиальных нулей и вообще значений в области К числу основных направлений в исследованиях Д.-ф. относятся: определение возможно более широкой области слева от прямой s= 1, где проблема порядка и средних значений Д.-ф. в критич. полосе; оценки числа нулей Д.-ф. на прямой s= 1/2 и вне этой прямой и т. д.

Первый нетривиальный результат о границе нулей Д.-ф. был получен Ш. Ж. Балле Пуссеном (Ch. J. La Vallee-Poussin) в 1896; он показал, что существует такая постоянная А>0, что

Дальнейшие продвижения в этом направлении связаны с приближенным уравнением (6) и развитием методов оценок тригонометрия, сумм.

Самый мощный метод оценок такого рода принадлежит И. М. Виноградову (см. Виноградова метод). Последняя (к 1978) граница области, свободной от нулей Д.-ф., получена И. М. Виноградовым в 1958 (см. [7]). Она имеет вид (7) с 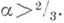Для простых чисел ей соответствует формула

Существует определенная связь между ростом модуля функции z(s) и отсутствием нулей в окрестности прямой s=1. Так, результат (7) с является следствием оценок

С другой стороны, известно (см. [4]), что

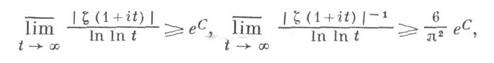
и, если верна гипотеза Римана, то эти пределы, соответственно, не больше, чем 2е ^С и

Порядок дзета-функции в критической полосе есть число h(s), означающее нижнюю границу таких чисел v, что z(s+it) = O(|t|^v). При s>1, h(s)=0, a при s<0 имеет место

Точные значения функции h(а)для неизвестны.

Простейшее предположение - Линделёфа гипотеза- состоит в том, что

Это эквивалентно утверждению, что

При 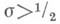справедлива оценка

Последняя известная (к 1978) оценка z(s) на прямой (см. [4]) далека от ожидаемой оценки (8); она имеет вид

Проблема среднего значения дзета-функции состоит в определении свойств функции

при для любого заданного s и k=1, 2, ... Результаты имеют приложения при изучении проблемы нулей Д.-ф. и непосредственно в теории чисел. Доказано, что (см. [4])

При (см. [4])

В случаях k>2 известно только, что при

где t_k(n) - число представлений п в виде кцелых положительных сомножителей, и что асимптотич. соотношение

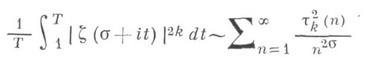
для s>¹/₂ является эквивалентом гипотезы Линделёфа. Важное место в теории Д.-ф. занимает проблема оценки функции N(s, T), означающей число нулей b+ig функции z(s) при b>s,В основе современных оценок N (s, Т )лежат теоремы о выпуклости средних значений аналитич. функций, применяемые к функции

Если для нек-poro Х=Х(s, Т),

I

при равномерно для s>a, где l(s).- положительная невозрастающая функция с ограниченной производной, а - постоянная, то

равномерно для

Известно также, что если при

то равномерно для

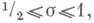
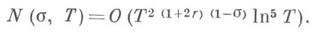
Эти два предложения позволили получить (см. [4]) следующие плотностные теоремы о нулях дзета-функции:

равномерно для

с привлечением иных соображений в [8] получена плотностная теорема:

если справедлива гипотеза Линделёфа, то

О нулях дзета-функции на прямой По гипотезе Римана, все нетривиальные нули Д.-ф. лежат на прямой Тот факт, что на. этой прямой Д.-ф. имеет бесконечно много нулей, впервые был доказан X. Харди в 1914 (см. [4]) на основе формулы Рамануджана

Последний результат принадлежит А. Сельбергу (A. Selberg, 1942; см. [4]): число N₀(T)нулей z(s), имеющих вид удовлетворяет неравенству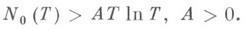

Это означает, что число нулей Д.-ф. на прямой s=¹/₂ имеет тот же порядок роста, что и число всех ее нетривиальных нулей:

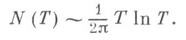
Относительно нулей Д.-ф. на этой прямой известны и другого рода результаты. Приближенное функциональное уравнение позволяет фактически вычислить (с нек-рой степенью точности) значения ближайших к действительной оси нулей z(s). На основе этого метода на ЭВМ вычислены нули z(s) в прямоугольнике . Их число равно 3,5.10⁶, и все они лежат на прямой Ординаты первых шести нулей с точностью до второго десятичного знака равны 14,13; 21,02; 25,01; 30,42; 32,93; 37,58.

Вообще, расстояние между соседними нулями z(s) оценивается теоремой Литлвуда (1924): для любого достаточно большого Тфункция z(s) имеет такой нуль b+ig, что

Обобщенная дзета-функция определяется для 0<a<1 рядом

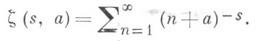
При a=1 она обращается в дзета-функцию Римана. Аналитическое продолжение на всю плоскость осуществляется формулой

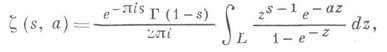
где интеграл берется по контуру L, представляющему собой путь из бесконечности по верхнему краю разреза положительной действительной оси до нек-рого фиксированного 0<r<2p, затем вдоль окружности радиуса rпротив часовой стрелки и снова в бесконечность по нижнему краю разреза. Функция z(s, а)регулярна всюду, кроме точки s=l, где она имеет простой полюс с вычетом, равным 1. Она играет важную роль в теории L-функций Дирихле (см. [9], [10]).

Дзета-функция Дедекинда - аналог дзета-функции Римана для полей алгебраич. чисел, введенный Р. Дедекиндом (см. [11]).

Пусть К- поле алгебраических чисел степени n=r₁+2r₂>1, где r₁- число действительных, r₂- число пар комплексно сопряженных полей в k;пусть далее D - дискриминант, h- число классов дивизоров, R-регулятор поля к, g- число содержащихся в ккорней из 1.

Дзета-функция Дедекинда z_k(s)поля k. определяется рядом

где U пробегает все целые отличные от нуля дивизоры поля к,- норма дивизора U. Этот ряд абсолютно и равномерно сходится при d>0, определяя аналитич. функцию, регулярную в полуплоскости s>1. При s>1 будет

где f(m) - число целых дивизоров поля kс нормой m, t _п (т)- число представлений тв виде пнатуральных сомножителей.

При s>1 имеет место тождество Эйлера где B пробегает все простые дивизоры поля k.

Основные свойства дзета-функции Дедекинда (см. [11]).

1) z_k(s) регулярна на всей комплексной плоскости, кроме точки s=l, где она имеет простой полюс с вычетом

2) z_k(s) удовлетворяет функциональному уравнению

где

3) При r=r₁+r₂-1>0 в точке s=0 функция z_k(s)имеет нуль порядка r; при r=0; в точках s=- 2v, v=l, 2, ..., дзета-функция Дедекинда z_k(s) имеет нули порядка r+1, в точках s=-2v-1 при r₂>0 - нули порядка r₂, а при r₂=0 не равна нулю. Это - тривиальные нули функции z_k(s).

4) Все остальные нули функции z_k(s) лежат в критич. полосе

Основная гипотеза состоит в том, что все нетривиальные нули функции z_k(s) находятся на прямой s=1/2. Установлено, что z_k(s) не имеет нулей на прямой s=1. Более того, существует абсолютная положительная постоянная Аи зависящая от параметров поля кпостоянная X, обладающие тем свойством, что

Вообще, в случае фиксированных параметров поля кдля z_k(s) имеют место многие результаты, аналогичные результатам для дзета-функции Римана. Однако в общем случае теория дзета-функции Дедекинда сложнее, поскольку она включает в себя и теорию Дирихле L-функций. Так, неизвестно (1978), имеют ли дзета-функции Дедекинда действительные нули между 0 и 1. Точная зависимость между дзета-функцией Дедекинда и L-рядами рационального поля имеет следующий вид. Пусть k*- минимальное поле Галуа, к-рому принадлежит к, Q- группа Галуа поля к*, h- число классов группы Q,c_i- простые характеры группы Q, Тогда

где z(s) - дзета-функция Римана, Lсуть L-ряды Артина, c_i=c_i(k)- целые положительные числа, к-рые определяются свойствами относительной группы Галуа поля к*. В частности, если к- круговое расширение, то k* = k, h=j(n), c_i=1, и L-ряды Артина становятся обычными L-рядами Дирихле.

Наряду с дзета-функцией Дедекинда z_k(s) рассматриваются и z_k(s; H_j) - дзета-функции Дедекинда класса дивизоров H_j поля к. Эти функции определяются теми же рядами, что и z_k(s), но только пробегает не все, а лишь целые дивизоры, к-рые принадлежат заданному классу Hj. Функции z_k(s; H_j )обладают свойствами, близкими свойствам z_k(s). Справедлива формула

Дзета-функции Дедекинда лежат в основе современной аналитич. теории дивизоров полей алгебраич. чисел. Здесь они играют такую же роль, какую играет дзета-функция Римана в теории чисел рационального поля.

Аналогом дзета-функции Дедекинда для полей алгебраич. функций от одного переменного с конечным полем констант является конгруэнц дзета-функция, или дзета-функция Артина- Шмидта (см. ниже Дзета-функция в алгебраической геометрии).

Лит.:[1] Эйлер Л., Введение в анализ бесконечно малых, 2 изд., т. 1, пер. с латин., М., 1961; [2] Чебышев П. <Л., Избр. математические труды, М.-Л., 1946; [3] Риман Б., Соч., пер. с нем., М.-Л., 1948; [4] Титчмарш Е. К., Теория дзета-функции Римана, пер. с англ., М., 1953; [5] Лаврик А. Ф., "Изв. АН СССР. Сер. матем.", 1968, т. 32, № 1, с. 134-85; [6] Виноградов И. М., Метод тригонометрических сумм в теории чисел, М., 1971; [7] его же, "Изв. АН СССР. Сер. матем.", 1958, т. 22, с. 161 - 64; [8] Монтгомери X. Л., "Математика", 1970, т. 14, № 5, с. 133-40; [9] Прахар К., Распределение простых чисел, пер. с нем., М., 1967; [10] Чудаков Н. Г., Введение в теорию L-функций Дирихле, М.-Л., 1947; [11] Несke E., Mathematische Werke, Gott., 1959.

А. Ф. Лаврик.

2) Д.-ф. в алгебраической геометрии - аналитическая функция комплексного переменного s, описывающая арифметику алгебраич. многообразий над конечными полями и схем конечного типа над Spec Z. Если X- такая схема, - множество ее замкнутых точек, а N(х)- число элементов поля вычетов k(x). точки то Д.-ф. z_X(s). задается эйлеровым произведением

Это произведение абсолютно сходится при Re s>dim X, допускает мероморфное продолжение в полуплоскости и имеет полюс в точке s=dim X(см. [10]). В случае если X=Spec Z, то z_X(s). есть дзета-функция Римана, а если Xконечна над Spec Z, то z_X(s) есть дзета-функция Дедекинда числового поля.

Наиболее изучена ситуация, когда Xявляется алгебраич. многообразием, определенным над конечным полем F_q. В этом случае

где deg х- степень поля (х)над полем F_q и вместо функции z_X(s)обычно рассматривают функцию Z_X(t)такую, что

Если у _п- число рациональных точек многообразия Xв поле F_qn, то оказывается (см. [14]), что

Такие Д.-ф. были введены впервые для случая алгебраич. кривых (по аналогии с полями алгебраич. чисел) в 1924 Э. Артином [1], к-рый заметил, что они являются рациональными функциями от tи для них в нек-рых случаях верен аналог гипотезы Римана о нулях. Этот аналог получил название гипотезы Артина. Для кривых рода 1 она была доказана X. Хассе (Н. Hasse) в 1933 (в случае рода 0 ситуация тривиальна), а для кривых произвольного рода - А. Вейлем (A. Weil) в 1940 при помощи результатов теории абелевых многообразий, созданной им в значительной мере для этой цели (см. [2], [14]).

А. Вейль [2] рассмотрел Д.-ф. произвольных алгебраич. многообразий и высказал гипотезы, обобщающие результаты, полученные к тому времени для кривых. Его исследования основаны на следующем замечании - множество точек многообразия X, рациональных над F_qa, является множеством неподвижных точек я-й степени Фробениуса эндоморфизма этого многообразия. Первая гипотеза Вейля состоит в том, что в категории алгебраич. многообразий над конечными полями существует теория когомологий, удовлетворяющая всем формальным свойствам, необходимым для получения Лефшеца формулы. Если {Н' (Х)}- группы когомологий такой теории, то из формулы Лефшеца следует, что где n=dim X,a P_i(t).- характеристич. многочлены отображений, индуцированных эндоморфизмом Фробениуса на Вейля когомологиях Н ⁱ (Х). В частности, функция z_X(t). рациональна.

Вторая гипотеза Вейля состоит в том, что функция z_X(t)должна удовлетворять функциональному уравнению, имеющему в случае гладкого проективного многообразия Xвид

где y_v- эйлерова характеристика, равная е(-1)ⁱ dim H'(X). (Эта гипотеза является формальным следствием существования теории когомологий.) Рациональность z-функции для любых Xдоказана Б. Дворком [6] методом, не использующим когомологий. Теория когомологий, предсказанная А. Вейлем, была создана А. Гротендиком (A. Grothendieck) в 1958 (см. Вейля когомологий, Топологизированная категория, l-адические когомологий). А. Гротендик вместе с М. Артином (М. Artin) доказал обе гипотезы Вейля для гладких проективных многообразий, причем многочлены P_i(t)имели, вообще говоря, целые Z-адические коэффициенты, зависящие от выбора простого l, положенного в основу теории. Предполагается, что на самом деле коэффициенты являются целыми числами, не зависящими от lи вообще от выбора теории когомологий. Это высказывание обычно наз. третьей гипотезой Вейля. Наконец, последняя - четвертая гипотеза Вейля относится к нулям a_i многочленов P_i(t), рассматриваемым как целые алгебраич. числа (гипотеза Римана):

Все эти гипотезы доказаны П. Делинем [4].

Основные применения гипотез Вейля в теории чисел относятся к изучению сравнений. Уже в случае кривых из теоремы Вейля вытекала наилучшая оценка для рациональной тригонометрич. суммы от одной переменной (см. [14]). Эти оценки были обобщены на суммы от любого числа переменных. Другим важным приложением этой теории являются оценки коэффициентов Фурье модулярных форм (проблема Рамануджана - Петерсона, см. [4], [15]).

Приведенные результаты являются на самом деле частными случаями гораздо более общих теорем, относящихся к произвольным L-функциям, к-рые связаны с представлениями групп Галуа накрытий многообразия Xили, более общо, с нек-рым l -адическим пучком на X(см. [5], [10]). Эти функции служат на произвольных схемах аналогом известных в теории алгебраич. чисел L-функций.

Пусть теперь X- схема конечного типа над Spec Zтакая, что ее общий слой является непустым алгебраич. многообразием над полем рациональных чисел Q. Существует предположение, что Д.-ф. z_X(s). имеют мероморфные продолжения на всю s-плоскость и удовлетворяют функциональному уравнению. Гипотетич. вид этого уравнения предложен в [11]. Доказать эту гипотезу удалось пока (1978) лишь в очень специальных случаях (рациональные поверхности, алгебраич. кривые, униформизуемые модулярными функциями, абелевы многообразия с комплексным умножением, см. [15]). Что касается аналога гипотезы Римана, то он в этой ситуации даже не сформулирован.

Новый круг идей в изучении Д.-ф. принесли работы Дж. Берча (J. Birch), П. Суиннертон-Дайера [12] и Дж. Тейта [13]. Чтобы сформулировать принадлежащие им гипотезы, следует заметить, что функция z_X(s)является произведением Д.-ф. z_Xp(s) слоев Х _р отображения X->Spec Z. Для последних, являющихся многообразиями над конечными полями, имеется, согласно первой гипотезе Вейля, разложение на многочлены. После перемножения этих разложений получается аналогичное представление для Д.-ф.

Гипотеза Берча и Суиннертон-Дайера предполагает, что порядок нуля функции в точке s=dim X-1 равен рангу группы рациональных точек многообразия Пикара Pic X(конечному, в силу теоремы Морделла - Вейля). Эта гипотеза, тем самым, предполагает справедливость гипотезы о мероморфном продолжении Д.-ф. В первоначальной форме гипотеза Берча и Суиннертон-Дайера была высказана для эллиптич. кривых над полем Qв результате изучения обширных таблиц для кривых с комплексным умножением [12]. В дальнейшем было высказано предположение о значении коэффициента при соответствующей степени переменной s в разложении функции в окрестности точки s=dim X-1. Предполагается,что он равен где [Ш] - предполагаемый конечным порядок группы Шафаревича - Тейта локально тривиальных главных однородных пространств многообразия Pic X,|det(a'_i, a_j)| - определитель билинейной формы на группе рациональных точек многообразия Pic X, получающийся из высоты точки, [Pic X_tors] и [Pic'X_tors] - порядки подгрупп кручения в группе рациональных точек на Pic Xи двойственном абелевом многообразии. Это выражение обобщает хорошо известное в теории алгебраич. чисел выражение для вычета дзета-функции Дедекинда в точке s=l. Одной из трудностей на пути к доказательству гипотезы Берча и Суиннертон-Дайера является тот факт, что группа Ш полностью не вычислена (1978) ни для одной кривой. Доказан аналог этой гипотезы для кривых, определенных над полем функций, однако и в этом случае пришлось предположить, конечность Брауэра группы, играющей здесь роль группы Ш (см. [5]).

Дж. Тейт [13], изучая действие группы Галуа на алгебраич. циклы многообразий, выдвинул гипотезы о полюсах функций при четных значениях i, а именно, что функция имеет в точке s= i+1 полюс порядка, равного рангу группы алгебраич. циклов коразмерности i. Это утверждение тесно связано с гипотезой Тейта об алгебраич. циклах. По поводу имеющихся подходов к доказательству этих гипотез, а также различных аргументов в их пользу см. [5], [7], [12], [13], [17].

Независимо от описываемого здесь понятия Д.-ф. в теории алгебраич. групп и автоморфных функций возникли и изучались Д.-ф., являющиеся преобразованиями Меллина модулярных форм. В 1967 А. Вейль заметил, что из общих гипотез о функции для эллиптич. кривой Xнад Qвытекает, что кривая Xуниформизуется модулярными функциями, а функция есть преобразование Меллина модулярной формы, отвечающей дифференциалу рода 1 на X. Это замечание привело к предположению о том, что функции любой схемы Xявляются преобразованиями Меллина подходящих модулярных форм. Основные результаты в этом направлении были получены Э. Жаке и Р. Ленглендсом (см. [7], [9]). В частности, они построили широкий класс рядов Дирихле, удовлетворяющих нек-рому функциональному уравнению и разлагающихся в эйлерово произведение, к-рые можно представить в виде преобразования Меллина модулярных форм на группе GL(2). Выполнимость условий их теоремы непосредственно связана с приведенными выше гипотезами об общих свойствах Д.-ф. Пока их удается проверить лишь для кривых, определенных над полем функций.

Начиная с 1970 под влиянием работ о р-адических. Д.-ф. полей алгебраич. чисел (см. [14]) возникает аналогичный подход и к Д.-ф. схем, главным образом эллиптич. кривых. Имеющиеся здесь проблемы, во многом, похожие на рассмотренные выше, отражены в [9]. Д.-ф. эллиптич. кривой над Qтесно связана с одномерной формальной группой кривой и они полностью друг друга определяют [16].

Лит.:[1] Artin E., "Math. Z.", 1924, Bd 19, S. 153-246; [2] Weil A., Sur les courbes algebriques et les varietes qui s'en deduisent, P., 1948; [3] eго же, "Bull. Amer. Math. Soc.", 1949, v. 55, № 5, p. 497 - 508; [4] Deligne P., "Publ. Math. IHES", 1974, t. 43, p. 273 - 307; [5] Dix exposes sur la cohomologie des schemes, Arast.-P., 1968; [6] Dwоrk В., в кн.: Proceedings of the International Congress of Mathematicians, Djursholm, 1963, p. 247-59; [7] ЖакеЭ., Ленгпендс Р., Автоморфные формы на GL (2), пер. с англ., М., 1973; [8] Манин Ю. И., "Успехи матем. наук", 1971, т. 26, в. 6, с. 7-71; [9] Modular functions of one variable, В., 1973; [101 С е р р Ж.-П., "Успехи матем. наук", 1965, т. 20, № 6, с. 19-26; [11] его же, "Математика", 1971, т. 15, № 1, с. 3-13; [121 Свиннертон-Дайер П., "Математика", 1969, т. 13,. № 5, с. 3-25; [13] Тэйт Д., "Успехи матем. наук", 1965, т.20,. № 6, с. 27-40; [14] Шафаревич И. Р., Дзета-функция, М., 1969; [15] Шимура Г., Введение в арифметическую теорию автоморфных функций, пер. с англ., М., 1973; [16] Xонда Т., "Математика", 1969, т. 13, № 6, с. 3-17; [17] Итоги, науки. Алгебра. Топология. Геометрия. 1970, М., 1971, с. 111-51..