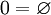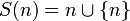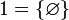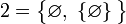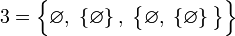- Натуральные числа
-
Натура́льные чи́сла — числа, возникающие естественным образом при счёте (как в смысле перечисления, так и в смысле исчисления).
Существуют два подхода к определению натуральных чисел — числа, используемые при:
- перечислении (нумеровании) предметов (первый, второй, третий…) — подход, общепринятый в большинстве стран мира (в том числе и в России).
- обозначении количества предметов (нет предметов, один предмет, два предмета…). Принят в трудах Бурбаки, где натуральные числа определяются как мощности конечных множеств.
Отрицательные и нецелые числа — натуральными числами не являются.
Множество всех натуральных чисел принято обозначать знаком
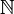 .
.Существует бесконечное множество натуральных чисел — для любого натурального числа найдется другое натуральное число, большее его.
 Натуральные числа можно использовать для счёта (одно яблоко, два яблока и т. п.).
Натуральные числа можно использовать для счёта (одно яблоко, два яблока и т. п.).Содержание
Определение
Аксиомы Пеано
Введём функцию S, которая сопоставляет числу x следующее за ним число.
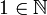 (1 является натуральным числом);
(1 является натуральным числом);- Если
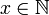 , то
, то 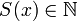 (Число, следующее за натуральным, также является натуральным);
(Число, следующее за натуральным, также является натуральным); 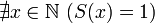 (1 не следует ни за каким натуральным числом);
(1 не следует ни за каким натуральным числом);- Если S(b) = a и S(c) = a, тогда b = c (если натуральное число a непосредственно следует как за числом b, так и за числом c, то b = c);
- Аксиома индукции. Пусть P(n) — некоторый одноместный предикат, зависящий от параметра — натурального числа n. Тогда:
-
- если P(1) и
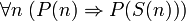 , то
, то 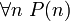
- (Если некоторое высказывание P верно для n = 1 (база индукции) и для любого n при допущении, что верно P(n), верно и P(n + 1) (индукционное предположение), то P(n) верно для любых натуральных n).
- если P(1) и
Теоретико-множественное определение
Согласно теории множеств, единственным объектом конструирования любых математических систем является множество.
Таким образом, и натуральные числа вводятся, исходя из понятия множества, по двум правилам:
Числа, заданные таким образом, называются ординальными.
Первые несколько ординальных чисел и соответствующие им натуральные числа:
Классы эквивалентности этих множеств относительно биекций также обозначают 0, 1, 2, ….
Замечание
Иногда, в иностранной и переводной литературе, в первой и третьей аксиомах заменяют 1 на 0. В этом случае ноль считается натуральным числом.
В русской литературе обычно ноль исключен из числа натуральных чисел
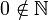 , а множество натуральных чисел с нулем обозначается как
, а множество натуральных чисел с нулем обозначается как 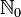 .
.Если в определение натуральных чисел включен ноль, то множество натуральных чисел записывается как
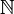 , а без нуля как
, а без нуля как 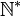 .
.Операции над натуральными числами
К замкнутым операциям (операциям, не выводящим результат из множества натуральных чисел) над натуральными числами относятся следующие арифметические операции:
- Сложение. Слагаемое + Слагаемое = Сумма
- Умножение. Множитель * Множитель = Произведение
- Возведение в степень ab, где a — основание степени и b — показатель степени. Если основание и показатель натуральны, то и результат будет являться натуральным числом.
Дополнительно рассматривают ещё две операции. С формальной точки зрения они не являются операциями над натуральными числами, так как не определены для всех пар чисел (иногда существуют, иногда нет).
- Вычитание. Уменьшаемое - Вычитаемое = Разность. При этом Уменьшаемое должно быть больше Вычитаемого (или равно ему, если считать 0 натуральным числом).
- Деление. Делимое / Делитель = (Частное, Остаток). Частное p и остаток r от деления a на b определяются так: a = p * b + r, причём
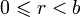 . Заметим, что именно последнее условие запрещает деление на ноль, так как иначе a можно представить в виде a = p * 0 + a, то есть можно было бы считать частным 0, а остатком = a.
. Заметим, что именно последнее условие запрещает деление на ноль, так как иначе a можно представить в виде a = p * 0 + a, то есть можно было бы считать частным 0, а остатком = a.
Следует заметить, что именно операции сложения и умножения являются основополагающими. В частности, кольцо целых чисел определяется именно через бинарные операции сложения и умножения.
Теоретико-множественные определения
Воспользуемся определением натуральных чисел как классов эквивалентности конечных множеств. Будем обозначать класс эквивалентности множества A относительно биекций как [A]. Тогда основные арифметические операции определяются следующим образом:
![[A] + [B] = [A \sqcup B]](/pictures/wiki/files/57/9c005a5f52f98d269b87d4262fe26710.png)
![[A] * [B] = [A \times B]](/pictures/wiki/files/55/76a9a15ae8e245d4716bfc12ac23c727.png)
- [A][B] = [AB]
где
 — дизъюнктное объединение множеств,
— дизъюнктное объединение множеств, 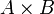 — прямое произведение, AB — множество отображений из B в A. Можно показать, что полученные операции на классах введены корректно, то есть не зависят от выбора элементов классов, и совпадают с индуктивными определениями.
— прямое произведение, AB — множество отображений из B в A. Можно показать, что полученные операции на классах введены корректно, то есть не зависят от выбора элементов классов, и совпадают с индуктивными определениями.Основные свойства
- Коммутативность сложения.
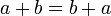
- Коммутативность умножения.
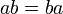
- Ассоциативность сложения.
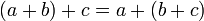
- Ассоциативность умножения.
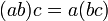
- Дистрибутивность умножения относительно сложения.
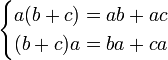
Алгебраическая структура
Сложение превращает множество натуральных чисел в полугруппу с единицей, роль единицы выполняет 0. Умножение также превращает множество натуральных чисел в полугруппу с единицей, при этом единичным элементом является 1. С помощью замыкания относительно операций сложения-вычитания и умножения-деления получаются группы целых чисел
 и рациональных положительных чисел
и рациональных положительных чисел 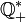 соответсвенно.
соответсвенно.Натуральные числа в русском языке
- Числа от 1 до 10 — один (1), два (2), три (3), четы́ре (4), пять (5), шесть (6), семь (7), во́семь (8), де́вять (9), де́сять (10).
- Числа от 11 до 20 — оди́ннадцать (11), двена́дцать (12), трина́дцать (13), четы́рнадцать (14), пятна́дцать (15), шестна́дцать (16), семна́дцать (17), восемна́дцать (18), девятна́дцать (19), два́дцать (20).
- Числа от 30 до 90 — три́дцать (30), со́рок (40), пятьдеся́т (50), шестьдеся́т (60), се́мьдесят (70), во́семьдесят (80), девяно́сто (90).
- Числа от 100 до 900 — сто (100), две́сти (200), три́ста (300), четы́реста (400), пятьсо́т (500), шестьсо́т (600), семьсо́т(700), восемьсо́т (800), девятьсо́т (900).
См. также
Ссылки
Wikimedia Foundation. 2010.