Ординал

Порядковое число, или трансфинитное число, или ординал в теории множеств — некоторое обобщение понятия натурального числа «за пределы бесконечности». Впервые введены Георгом Кантором в 1897 году с целью классификации вполне упорядоченных множеств. Играют ключевую роль в доказательстве многих теорем теории множеств, в особенности в связи со связанным с ними принципом трансфинитной индукции.

Определение

Порядковые числа допускают различные варианты в том или ином смысле эквивалентных определений. Одна из современных формулировок определения порядкового числа по фон Нейману выглядит следующим образом:

• Назовём множество транзитивным, если каждый элемент x является подмножеством x: $\mathrm{Trans}(x) \Leftrightarrow \forall t (t \in x \rightarrow t \subseteq x)$.
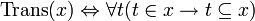• Удовлетворяющее аксиоме фундирования множество называется ординалом, или порядковым числом, если оно само и каждый его элемент транзитивны: $\mathrm{Ord}(x) \Leftrightarrow \mathrm{Trans}(x) \wedge \forall t (t \in x \rightarrow \mathrm{Trans}(t))$.

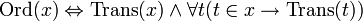Заметим, что аксиома фундирования существенно используется в этом определении, что необходимо учитывать при работе с аксиоматическими системами, отличными от системы Цермело — Френкеля.

Свойства

• Если α — порядковое число, то каждый элемент α — порядковое число.
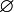• $\varnothing$ — порядковое число.
• Если α — порядковое число, то 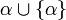$\alpha \cup \{ \alpha \}$ — порядковое число (терм 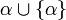$\alpha \cup \{ \alpha \}$ обозначают при этом как α + 1). Ординалы, совпадающие с α + 1 для некоторого α, называются непредельными ординалами, в отличие от предельных.
• Множество натуральных чисел ω — порядковое число, множества ω + 1, ω + 2, ω + ω, … — порядковые числа.
• Всякое множество x порядковых чисел вполне упорядочено по отношению 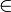$\in$, при этом 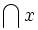$\bigcap x$ — наименьший элемент любого множества порядковых чисел, 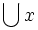$\bigcup x$ — порядковое число, большее или равное любому из чисел во множестве x.
• Не существует множества всех порядковых чисел. Иначе говоря, совокупность всех порядковых чисел является собственно классом.

Арифметика ординалов

См. также

Литература