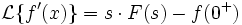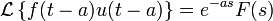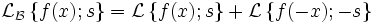- Лапласа преобразование
-
Преобразова́ние Лапла́са — интегральное преобразование, связывающее функцию
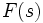 комплексного переменного (изображение) с функцией
комплексного переменного (изображение) с функцией 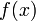 действительного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения.
действительного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения.Одной из особенностей преобразования Лапласа, которые предопределили его широкое распространение в научных и инженерных расчётах, является то, что многим соотношениям и операциям над оригиналами соответствуют более простые соотношения над их изображениями. Так свёртка двух функций сводится в пространстве изображений к операции умножения, а линейные дифференциальные уравнения становятся алгебраическими.
Содержание
Определение
Прямое преобразование Лапласа
Преобразованием Лапласа функции действительной переменной
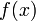 , называется функция
, называется функция 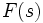 комплексной переменной
комплексной переменной  , такая что:
, такая что:Правая часть этого выражения называется интегралом Лапласа.
Обратное преобразование Лапласа
Обратным преобразованием Лапласа функции комплексного переменного
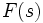 , называется функция
, называется функция 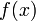 действительного переменного, такая что:
действительного переменного, такая что:где
 — некоторое вещественное число (см. условия существования). Правая часть этого выражения называется интегралом Бромвича.
— некоторое вещественное число (см. условия существования). Правая часть этого выражения называется интегралом Бромвича.Двустороннее преобразование Лапласа
Двустороннее преобразование Лапласа — обобщение на случай задач, в которых для функции
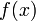 участвуют значения x < 0
участвуют значения x < 0Двусторонее преобразование Лапласа определяется следующим образом:
Дискретное преобразование Лапласа
Применяется в сфере систем компьютерного управления. Дискретное преобразование Лапласа может быть применено для решётчатых функций.
Различают -преобразование и
-преобразование и  -преобразование.
-преобразование. -преобразование
-преобразование
Пусть
 — решётчатая функция, то есть значения этой функции определены только в дискретные моменты времени
— решётчатая функция, то есть значения этой функции определены только в дискретные моменты времени  , где
, где 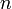 — целое число, а
— целое число, а  — период дискретизации.
— период дискретизации.
Тогда применяя преобразование Лапласа получим:

 -преобразование
-преобразование
Если применить следующую замену переменных:
 ,
,
получим Z-преобразование:

Свойства и теоремы
- Абсолютная сходимость
Если интеграл Лапласа абсолютно сходится при σ = σ0, то есть существует предел
 ,
,
то он сходится абсолютно и равномерно для
 и F(s) — аналитичная функция при
и F(s) — аналитичная функция при  (
( — действительная часть комплексной переменной s). Точная нижняя грань σa множества чисел σ, при которых это условие выполняется, называется абсциссой абсолютной сходимости преобразования Лапласа для функции f(x).
— действительная часть комплексной переменной s). Точная нижняя грань σa множества чисел σ, при которых это условие выполняется, называется абсциссой абсолютной сходимости преобразования Лапласа для функции f(x).- Условия существования прямого преобразования Лапласа
Преобразование Лапласа
 существует в смысле абсолютной сходимости в следующих случаях:
существует в смысле абсолютной сходимости в следующих случаях:- Случай
 : преобразование Лапласа существует, если существует интеграл
: преобразование Лапласа существует, если существует интеграл 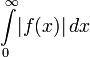
- Случай σ > σa: преобразование Лапласа существует, если интеграл
 существует для каждого конечного x1 > 0 и
существует для каждого конечного x1 > 0 и  для
для 
- Случай σ > 0 или σ > σa (какая из границ больше): преобразование Лапласа существует, если существует преобразование Лапласа для функции f'(x) (производная к f(x)) для σ > σa.
Примечание: это достаточные условия существования.
- Условия существования обратного преобразования Лапласа
Для существования обратного преобразования Лапласа достаточно выполнение следующих условий:
1. Если изображение F(s) — аналитичная функция для
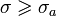 и имеет порядок меньше −1, то обратное преобразование для неё существует и непрерывно для всех значений аргумента, причём
и имеет порядок меньше −1, то обратное преобразование для неё существует и непрерывно для всех значений аргумента, причём 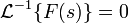 для
для 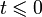
2. Пусть
![F(s) = \varphi[F_1(s), F_2(s), \dots, F_n(s)]](/pictures/wiki/files/49/1a32600b5e18e73de1cdff577d64fe2e.png) , так что
, так что  аналитична относительно каждого zk и равна нулю для
аналитична относительно каждого zk и равна нулю для 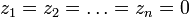 , и
, и 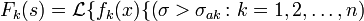 , тогда обратное преобразование существует и соответствующее прямое преобразование имеет абсциссу абсолютной сходимости.
, тогда обратное преобразование существует и соответствующее прямое преобразование имеет абсциссу абсолютной сходимости.Примечание: это достаточные условия существования.
- Теорема о свёртке
Преобразованием Лапласа свёртки двух оригиналов является произведение изображений этих оригиналов.
- Умножение изображений

Левая часть этого выражения называется интегралом Дюамеля, играющим важную роль в теории динамических систем.
- Дифференцирование и интегрирование оригинала
Изображением по Лапласу первой производной от оригинала по аргументу является произведение изображения на аргумент последнего за вычетом оригинала в нуле справа.
В более общем случае (производная n-го порядка):
Изображением по Лапласу интеграла от оригинала по аргументу является изображение оригинала деленное на свой аргумент.
- Дифференцирование и интегрирование изображения
Обратное преобразование Лапласа от производной изображения по аргументу есть произведение оригинала на свой аргумент, взятое с обратным знаком.
Обратное преобразование Лапласа от интеграла изображения по аргументу есть оригинал этого изображения, деленный на свой аргумент.
- Запаздывание оригиналов и изображений. Предельные теоремы
Запаздывание изображения:
Запаздывание оригинала:
Примечание: u(x) — Функция Хевисайда.
Теоремы о начальном и конечном значении (предельные теоремы):
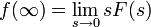 , все полюсы в левой полуплоскости
, все полюсы в левой полуплоскости
Теорема о конечном значении очень полезна, так как описывает поведение оригинала на бесконечности с помощью простого соотношения. Это, к примеру, используется для анализа устойчивости траектории динамической системы.
- Другие свойства
Линейность
Умножение на число
Прямое и обратное преобразование Лапласа некоторых функций
Ниже представлена таблица преобразования Лапласа для некоторых функций.
№ Функция Временная область

Частотная область
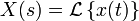
Область сходимости
для причинных систем1 идеальное запаздывание 

1a единичный импульс 


2 запаздывание n-го порядка с частотным сдвигом 
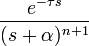

2a степенная n-го порядка 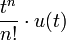


2a.1 степенная q-го порядка 
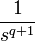

2a.2 единичная функция 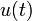


2b единичная функция с запаздыванием 


2c «ступенька скорости» 


2d n-го порядка с частотным сдвигом 


2d.1 экспоненциальное затухание 
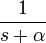

3 экспоненциальное приближение 


4 синус 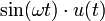


5 косинус 
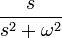

6 гиперболический синус 
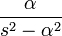

7 гиперболический косинус 


8 экспоненциально затухающий
синус


9 экспоненциально затухающий
косинус


10 корень n-го порядка ![\sqrt[n]{t} \cdot u(t)](/pictures/wiki/files/52/486b3056c275d0abfe2730f87a747f9f.png)
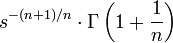

11 натуральный логарифм 
![- { t_0 \over s} \ [ \ \ln(t_0 s)+\gamma \ ]](/pictures/wiki/files/52/45e874340427d4d5e74e12ede79de487.png)

12 функция Бесселя
первого рода
порядка n



13 модифицированная функция Бесселя
первого рода
порядка n


14 функция Бесселя
второго рода
нулевого порядка
15 модифицированная функция Бесселя
второго рода,
нулевого порядка
16 функция ошибок 
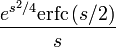

Примечания к таблице:  — функция Хевисайда.
— функция Хевисайда. — дельта-функция.
— дельта-функция. — гамма-функция.
— гамма-функция.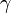 — постоянная Эйлера — Маскерони.
— постоянная Эйлера — Маскерони. , — вещественная переменная.
, — вещественная переменная. — комплексная переменная.
— комплексная переменная. ,
,  ,
,  и
и  — вещественные числа.
— вещественные числа. — целое число.
— целое число.- Причинная система — система, в которой импульсная передаточная функция h(t) равна нулю для любого момента времени
 .
.
Применения преобразования Лапласа
Преобразование Лапласа находит широкое применение во многих областях математики (операционное исчисление), физики и техники.
- Решение систем дифференциальных и интегральных уравнений — с помощью преобразования Лапласа легко переходить от сложных понятий математического анализа к простым алгебраическим соотношениям.
- Расчёт передаточных функций динамических систем, таких, к примеру, как аналоговые фильтры.
- Расчёт выходных сигналов динамических систем в теории управления и обработке сигналов — так как выходной сигнал линейной стационарной системы равен свёртке её импульсной характеристики с входным сигналом, преобразование Лапласа позволяет заменить эту операцию на простое умножение.
- Расчёт электрических схем. Производится путём решения дифференциальных уравнений, описывающих схему операторным методом.
- Решение нестационарных задач математической физики.
Связь с другими преобразованиями
Фундаментальные связи
Практически все интегральные преобразования имеют схожую природу и могут получаться одно из другого через выражения соответствия. Многие из них являются частными случаями других преобразований. Далее даны формулы, связывающие преобразования Лапласа с некоторыми другими функциональными преобразованиями.
Преобразование Лапласа-Карсона
Преобразование Лапласа-Карсона получается из преобразования Лапласа путём домножения его на комплексную переменную.
Двустороннее преобразование Лапласа
Двустороннее преобразование Лапласа
 связано с односторонним с помощью следующей формулы:
связано с односторонним с помощью следующей формулы:Преобразование Фурье
Непрерывное преобразование Фурье эквивалентно двустороннему преобразованию Лапласа с комплексным аргументом s = iω:
Примечание: в этих выражениях опущен масштабирующий множитель
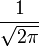 , который часто включается в определения преобразования Фурье.
, который часто включается в определения преобразования Фурье.Связь между преобразованиями Фурье и Лапласа часто используется для того, чтобы определить частотный спектр сигнала или динамической системы.
Преобразование Меллина
Преобразование Меллина и обратное преобразование Меллина связаны с двусторонним преобразованием Лапласа простой заменой переменных. Если в преобразовании Меллина
положим θ = e − x, то получим двустороннее преобразование Лапласа.
Z-преобразование
Z-преобразование — это преобразование Лапласа решётчатой функции, производимое с помощью замены переменных:
где
 — период дискретизации, а
— период дискретизации, а  — частота дискретизации сигнала. Связь выражается с помощью следующего соотношения:
— частота дискретизации сигнала. Связь выражается с помощью следующего соотношения:Преобразование Бореля
Интегральная форма преобразования Бореля идентична преобразованию Лапласа, существует также обобщённое преобразование Бореля, с помощью которого использование преобразования Лапласа распространяется на более широкий класс функций.
Библиография
- Ван-дер Поль Б., Бремер Х. Операционное исчисление на основе двустороннего преобразования Лапласа.-М., ИЛ, 1952
- Диткин В. А., Прудников А. П. Интегральные преобразования и операционное исчисление.- М, Физматгиз, 1961
- Диткин В. А., Прудников А. П. Интегральные преобразования и операционное исчисление.- М, Физматгиз, 1974.-542 с.
- Карслоу Х., Егер Д. Операционные методы в прикладной математике.-М., ИЛ, 1948
- Кожевников Н. И., Краснощекова Т. И., Шишкин Н. Е. Ряды и интегралы Фурье. Теория поля. Аналитические и специальные функции. Преобразования Лапласа.-М., Наука, 1964
- Краснов М. Л., Макаренко Г. И. Операционное исчисление. Устойчивость движения.-М., Наука, 1964.-103 с.
- Микусинский Я. Операторное исчисление.-М., ИЛ, 1956
- Романовский П. И. Ряды Фурье. Теория поля. Аналитические и специальные функции. Преобразования Лапласа.-М., Наука, 1980.-336 с.
См. также
Внешние ссылки
Wikimedia Foundation. 2010.