Функция Хевисайда

Единичная функция Хевисайда

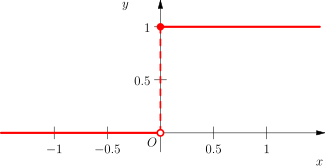
Функция Хевисайда (единичная ступенчатая функция, функция единичного скачка, включенная единица) — кусочно-постоянная функция, равная нулю для отрицательных значений аргумента и единице — для положительных. В нуле эта функция, вообще говоря, не определена, однако её обычно доопределяют в этой точке некоторым числом, чтобы область определения функции содержала все точки действительной оси. Чаще всего неважно, какое значение функция принимает в нуле, поэтому могут использоваться различные определения функции Хевисайда, удобные по тем или иным соображениям, например^[1]

$\theta(x)=\begin{cases} 0, & x<0; \\ \dfrac{1}{2}, & x=0; \\ 1, & x>0.\end{cases}$

Другое распространённое определение:

$\theta(x)=\begin{cases} 0, & x<0; \\ 1, & x\geqslant 0.\end{cases}$

Функция Хевисайда широко используется в математическом аппарате теории управления и теории обработки сигналов для представления сигналов, переходящих в определённый момент времени из одного состояния в другое. В математической статистике эта функция применяется, например, для записи эмпирической функции распределения. Названа в честь Оливера Хевисайда.

Функция Хевисайда является первообразной функцией для дельта-функции Дирака, $\theta'=\delta$, это также можно записать как:

$\theta(x)=\int\limits_{-\infty}^x\!\delta(t)\,dt.$

Дискретная форма

Можно определить дискретную функцию Хевисайда как функцию от целого аргумента $n$:

$\theta[n]=\begin{cases}0, & n<0; \\ 1, & n\geqslant 0,\end{cases}$

где $n$ — целое число.

Дискретный единичный импульс является первой разностью дискретной функции Хевисайда:

$\delta[n]=\theta[n]-\theta[n-1].$

Аналитические формы

Для более удобного использования функцию Хевисайда можно аппроксимировать с помощью непрерывной функции:

$\theta(x)\approx\frac{1}{2}+\frac{1}{2}\mathrm{th}\,kx=\frac{1}{1+e^{-2kx}},$

где большему $k$ соответствует более крутой подъём функции в точке $x=0$. Если принять $\theta(0)=1/2$, уравнение можно записать в предельной форме:

$\theta(x)=\lim_{k\to\infty}\frac{1}{2}(1+\mathrm{th}\,kx)=\lim_{k\to\infty}\frac{1}{1+e^{-2kx}}.$

Существует несколько других аппроксимаций непрерывными функциями:

$\theta(x)=\lim_{k\to\infty}\left(\frac{1}{2}+\frac{1}{\pi}\mathrm{arctg}\,kx\right);$

$\theta(x)=\lim_{k\to\infty}\left(\frac{1}{2}+\frac{1}{2}\,\mathrm{erf}\,kx\right).$

Запись

Часто используется и бывает полезной интегральная форма записи единичной функции:

$\theta(x)=-\lim_{\varepsilon\to 0^+}\frac{1}{2\pi i}\int\limits_{-\infty}^\infty\frac{1}{\tau+i\varepsilon}e^{-ix\tau}\,d\tau.$

$\theta(0)$

Значение функции в нуле часто задаётся как $\theta(0)=0$, $\theta(0)=1/2$ или $\theta(0)=1$. $\theta(0)=1/2$ — наиболее употребительный вариант, поскольку по соображениям симметрии в точке разрыва первого рода удобно доопределять функцию средним арифметическим соответствующих односторонних пределов, кроме того в этом случае функция Хевисайда связана с функцией знака:

$\theta(x)=\frac{1}{2}(1+\sgn x)=\begin{cases} 0, & x<0; \\ \dfrac{1}{2}, & x=0; \\ 1, & x>0.\end{cases}$

Значение в нуле может явно указываться в записи функции:

$\theta_n(x)=\begin{cases}0, & x<0; \\ n, & x=0; \\ 1, & x>0.\end{cases}$

Преобразование Фурье

Производная функции Хевисайда равна дельта-функции (то есть функция Хевисайда — первообразная дельта-функции):

$\theta(x)=\int\limits_{-\infty}^x\delta(t)\,dt$.

Следовательно, применив преобразование Фурье к первообразной дельта-функции $~\theta(t)$, получим её изображение вида:

$\frac{1}{2\pi i\omega}+\frac{1}{2}\delta(\omega),$

то есть:

$\theta(t)=\int\limits_{-\infty}^{+\infty}\left(\frac{1}{2\pi i\omega}+\frac{1}{2}\delta(\omega)\right)e^{i\omega t}\,d\omega$

(второй член — соответствующий нулевой частоте в разложении — описывает постоянное смещение функции Хевисайда вверх; без него получилась бы нечётная функция).

См. также

• Прямоугольная функция
• Дельта-функция
• Переходная функция

Примечания

1. ↑ В теории автоматического управления и теории операторов Лапласа часто обозначается как $\scriptstyle{\eta(x)}$. См., например,
   Волков И. К., Канатников А. Н. Интегральные преобразования и операционное исчисление: Учеб. для вузов / Под ред. B. C. Зарубина, А. П. Крищенко. — 2-е изд. — М.: Изд-во МГТУ им. Н. Э. Баумана, 2002. — 228 с. — (Математика в техническом университете; Вып. XI). — ISBN 5-7038-1273-9.