- Кубические уравнения
-
Куби́ческое уравне́ние — полиномиальное уравнение третьей степени, канонический вид которого
- ax3 + bx2 + cx + d = 0,
где
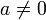 .
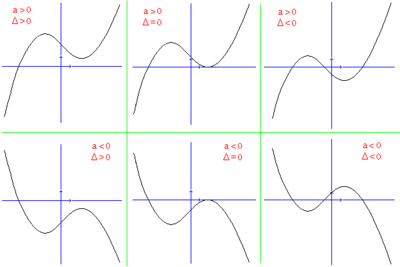
.Для графического анализа кубического уравнения в декартовой системе координат используется кубическая парабола.
Заменяя в этом уравнении x новым неизвестным y, связанным с x равенством
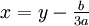 , уравнение можно привести к более простому (каноническому) виду:
, уравнение можно привести к более простому (каноническому) виду:- y3 + py + q = 0,
где
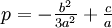 ,
,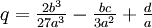 ,
,
Корни уравнения
Число x, обращающее уравнение в тождество, называется корнем или решением уравнения. Оно является также корнем многочлена третьей степени, стоящего в левой части канонической записи.
Над полем комплексных чисел, согласно основной теореме алгебры, кубическое уравнение всегда имеет 3 корня (с учётом кратности).
Так как каждый вещественный многочлен нечётной степени имеет хотя бы один вещественный корень, все возможные случаи состава корней кубического уравнения исчерпывается тремя, описанными ниже. Эти случаи легко различаются с помощью дискриминанта
-
- Δ = − 4b3d + b2c2 − 4ac3 + 18abcd − 27a2d2.
Итак, возможны только три случая:
- Если Δ > 0, тогда уравнение имеет три различных вещественных корня.
- Если Δ < 0, то уравнение имеет один вещественный и пару комплексно сопряжённых корней.
- Если Δ = 0, тогда хотя бы два корня совпадают. Это может быть когда уравнение имеет двойной вещественный корень и ещё один отличный от них вещественный корень; либо, все три корня совпадают, образуя корень кратности 3. Разделить эти два случая помогает результант кубического уравнения и его второй производной: у многочлена есть корень кратности 3 тогда и только тогда, когда указанный результант так же равен нулю.
Методы решения
См. также
Wikimedia Foundation. 2010.
