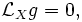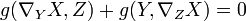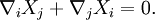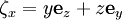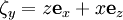- Векторное поле Киллинга
-
Поле Киллинга — векторное поле скоростей (локальной) однопараметрической группы движений риманова или псевдориманова многообразия. Другими словами, поток, который генерируется векторным полем Киллинга, задает непрерывное однопараметрическое семейство движений многообразия, то есть преобразований, относительно которых метрический тензор остается инвариантным. В частности, если метрический тензор gμν в некоторой системе не зависит от одной из координат xμ, тогда векторное поле вдоль этой координаты
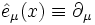 будет полем Киллинга.
будет полем Киллинга.Векторы Киллинга в физике указывают на симметрию физической модели и помогают найти сохраняющиеся величины, такие как энергия, импульс или спин. В теории относительности, например, если метрический тензор не зависит от времени, то в пространстве-времени существует времениподобный вектор Киллинга, с которым связана сохраняющаяся величина — энергия гравитационного поля.
Название дано в честь немецкого математика Вильгельма Киллинга (Wilhelm Killing), открывшего группы Ли и многие их свойства параллельно с Софусом Ли.
Содержание
Определение
Векторное поле X на M называется полем Киллинга если оно удовлетворяет следующему уравнению:
где
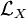 — производная Ли по направлению X, a g — риманова метрика на M.
— производная Ли по направлению X, a g — риманова метрика на M.Это уравнение можно переписать через связность Леви-Чивита:
для любых полей Y и Z.
В терминах локальных координат:
Свойства
- Векторное поле X является полем Киллинга тогда и только тогда, когда сужение X на любую геодезическую является полем Якоби.
- Для задания поля Киллинга достаточно указать его значение, плюс значения всех его (ковариантных) производных первого порядка, всего в одной точке. Из этой точки векторное поле может быть продолжено на все многообразие.
- Скобка Ли, или коммутатор двух полей Киллинга дает опять поле Киллинга. Таким образом, поля Киллинга образуют подалгебру бесконечномерной алгебры Ли всех (дифференцируемых) векторных полей на многообразии. Эта подалгебра является алгеброй Ли группы движений многообразия.
- Линейная комбинация полей Киллинга тоже является полем Киллинга.
- Иллюстрация сложения полей Киллинга на плоскости. Поле вращений вокруг начала координат + поле параллельного переноса вдоль оси y = поле вращений вокруг центра, смещенного относительно начала координат вдоль оси x:
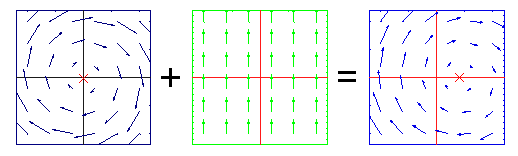
Все три поля являются полями движений плоскости.
- Иллюстрация сложения полей Киллинга на плоскости. Поле вращений вокруг начала координат + поле параллельного переноса вдоль оси y = поле вращений вокруг центра, смещенного относительно начала координат вдоль оси x:
- Если кривизна Риччи компактного многообразия отрицательна то на нём нет нетривиальных (то есть не равных тождественно нулю) полей Киллинга .
- Если секционная кривизна компактного многообразия положительная и размерность чётная, то поле Киллинга должно иметь нуль.
Примеры
- На евклидовой плоскости существует три линейно независимых поля Киллинга
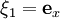 ,
, 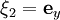 ,
, 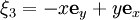
- Первые два поля Киллинга отвечают однопараметрическим подгруппам сдвигов вдоль осей x и y, а последнее — подгруппе вращений вокруг начала координат. Различные комбинации из этих трех подгрупп исчерпывают всевозможные движения плоскости.
- В трёхмерном евклидовом пространстве
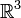 существует шесть линейно независимых полей Киллинга:
существует шесть линейно независимых полей Киллинга:
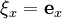 ,
, 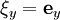 ,
, 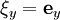
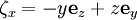
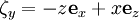
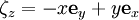
- Последние три поля ζx, ζy и ζz являются также полями Киллинга на сфере
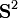 (это становится очевидным если рассматривать ее погруженной в трехмерное пространство).
(это становится очевидным если рассматривать ее погруженной в трехмерное пространство). - Однолистный гиперболоид, задаваемый уравнением x2 + y2 − z2 = 1, погруженный в пространство Минковского с метрикой ds2 = dx2 + dy2 − dz2, имеет три линейно независимых поля Киллинга, подобных полям Киллинга на сфере:
Вариации и обобщения
- Конформные поля Киллинга, определяются формулой
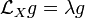
для некоторого скаляра λ. Они являются производными однопараметрических семейств конформных отображений. - Конформные тензорные поля Киллинга: симметричные тензорные поля T, такие что симметризация
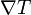 равна нулю.
равна нулю. - Антисимметричное тензорное поле Киллинга — Яно, часто представяемое, как «корень квадратный из симметричного тензорного поля Киллинга». Симметрия, описываемая тензорами Киллинга и Киллинга — Яно, существует во вращающихся черных дырах Керра, а также некоторых ее обобщениях. Наличие подобной симметрии объясняет, почему разделяются переменные в уравнениях движения классической и квантовой релятивистской механики: Гамильтона — Якоби, волновом, Клейна — Гордона, Дирака и др. (см. о тензорх Киллинга и Киллинга — Яно: Алексей Борисович Гаина. Квантовые частицы в полях Эйнштейна — Максвелла/Кишинев. Штиинца. 1989)
См. также
Wikimedia Foundation. 2010.