- МЕТРИКА ПРОСТРАНСТВА-ВРЕМЕНИ
- МЕТРИКА ПРОСТРАНСТВА-ВРЕМЕНИ
-
в теории относительности, задаёт расстояния (интервалы) между точками пространства-времени (событиями) и, т. о., полностью определяет геометрические свойства четырёхмерного пространства-времени. (см. ОТНОСИТЕЛЬНОСТИ ТЕОРИЯ, ТЯГОТЕНИЕ).
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- МЕТРИКА ПРОСТРАНСТВА-ВРЕМЕНИ
-
- основная геом. структура, к-рой наделяется пространственно-временное многообразие в специальной и общей теории относительности; определяется заданием поля симметричного ковариантного тензора 2-го ранга с отличным от нуля определителем - метрического тензора.
Метрич. тензор в спец. теории относительности имеет вид
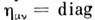(1, -1, -1, -1) (псевдоэвклидова метрика сигнатуры -2); пространственно-временное многообразие с такой метрикой наз. пространством-временем Минковского. В общей теории относительности вводится метрич. тензор 
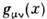более общего вида, удовлетворяющий, однако, требованию, <чтобы в достаточно малой окрестности любой заданной пространственно-временной точки c спец. выбором координат 
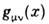можно было свести к 
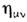; такое пространство-время (п.-в.) является пссвдоримановым пространством сигнатуры -2.M. п.-в. задаёт квадрат интервала- "расстояния" между событиями, с к-рыми сопоставляются точки п.-в.:
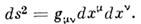
При преобразованиях пространственно-временных координат метрич. тензор, вообще говоря, изменяется (такие преобразования включают и переход к произвольно движущейся в каждой точке системе отсчёта) так, чтобы величина ds~ оставалась инвариантной. Существуют, однако, преобразования, оставляющие метрич. тензор фор-минвариантным (преобразования изометрии), они выражают собой геом. симметрии п.-в., обусловленные физ. содержанием теории. Так, метрич. тензор п.-в. Минковского в спец. теории относительности не изменяется при преобразованиях координат из группы Пуанкаре, включающих переносы начала отсчёта пространственных координат и времени, повороты пространственных осей и Лоренца преобразования. Поскольку последние интерпретируются как описывающие переход от одной инерц. системы отсчёта к другой, инвариантность метрики п.-в. Минковского означает, что ур-ния, записанные в лоренц-ковариантной форме, будут автоматически удовлетворять относительности принципу Эйнштейна.
В общей теории относительности существование преобразований, не изменяющих M. п.-в., возможно лишь при наличии соответствующих симметрии гравитац. поля. Так, метрич. тензор п.-в. Шварцшильда инвариантен относительно пространственных поворотов и временных сдвигов, что отражает центр, характер гравитац. поля и его статичность; структура метрич. тензора в моделях Фридмана, описывающих крупномасштабную структуру п.-в. Вселенной в целом, отражает факт однородности и изотропии Вселенной в больших масштабах (см. Тяготение). Если нек-рое преобразование изометрии порождается векторным полем, то такое векторное поле наз. полем Киллинга (W. Killing, 1892) и удовлетворяет ур-нию
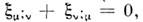где точкой с запятой обозначена ковариантная производная, согласованная с метрикой.Следует иметь в виду, что M. п.-в. отражает не только характер гравитац. поля, но и выбор системы координат в п.-в. (системы отсчёта). Так, переход к криволинейным координатам в п.-в. Минковского (к ускоренной системе отсчёта) приводит к метрич. тензору общего вида, однако собственно гравитац. поля в этом случае нет. Истинное гравитац. поле связано с тензором кривизны Римана - Кристоффеля, к-рый равен нулю в плоском п.-в. в любой системе отсчёта.
M. п.-в. в случае слабого гравитац. поля непосредственно связана с ньютоновским гравитац. потенциалом
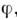а именно: 
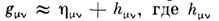малые добавки, характеризующие отклонение метрики от плоской, причём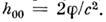 
Помимо задания расстояний в пространстве-времени, M. п.-в. служит для определения "длины" 4-векторов А ,
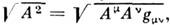а также позволяет ввести операции поднятия и опускания индексов у векторов и тензоров. Определитель метрич. тензора задаёт инвариантный элемент объёма в п.-в.:
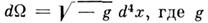- определитель метрич. тензора.Лит. см. при ст. Относительности теория, Тяготение. ^ Д. В. Галъцов.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
