- Разложение Хана-Жордана
-
Заряд — вещественнозначная конечно-аддитивная функция множества, определённая на некоторой σ-алгебре, (например, борелевских подмножеств).
В отличие от обычной меры под которой, обычно понимают положительную σ-аддитивную функцию множества, заряд может принимать и отрицательные значения и необязательно быть счётно-аддитивным.
При этом, термин заряд и конечно-аддитивная мера это синонимы.
Множество всех зарядов над произвольным множеством X c сигма-алгеброй Σ принято обозначать
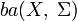 .
.Содержание
Связанные определения
- Положительный заряд
 называется чисто конечно аддитивным, если для любой положительной счётно-аддитивной меры μ из
называется чисто конечно аддитивным, если для любой положительной счётно-аддитивной меры μ из  вытекает, что μ = 0.
вытекает, что μ = 0.
- Произвольный заряд чисто конечно аддитивен если таковы заряды ν + и ν − .
Свойства
- Множество всех зарядов образует нормированную решётку и даже более, того K-пространство.
- Для любого заряда ν имеется положительную часть
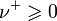 и отрицательную часть
и отрицательную часть 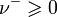 . Имеет место разложение Хана — Жордана ν = ν + − ν − , в силу которого свойства зарядов могут быть выражены в терминах теории меры.
. Имеет место разложение Хана — Жордана ν = ν + − ν − , в силу которого свойства зарядов могут быть выражены в терминах теории меры. - Пусть
 .
.
Для любой заряда ν единственным образом представим ввиде суммы ν = ν1 + ν2, где ν1 абсолютно непрерывна относительно μ и ν2 дизъюнктна μ. Такое представление меры ν принято назвать разложение по Лебегу. - Любой заряд
 единственным образом представим в виде суммы ν = νca + νpfa, где νca произвольная счётно-аддитивная мера, а νpfa произвольная чисто конечно-аддитивный заряд. Такое разложение иногда называют разложением Иосиды — Хьюита.
единственным образом представим в виде суммы ν = νca + νpfa, где νca произвольная счётно-аддитивная мера, а νpfa произвольная чисто конечно-аддитивный заряд. Такое разложение иногда называют разложением Иосиды — Хьюита. - Пространство
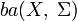 является топологически сопряжённым к пространству измеримых и ограниченных функций заданных над данным измеримым пространством.
является топологически сопряжённым к пространству измеримых и ограниченных функций заданных над данным измеримым пространством.
История
Термин заряд был впервые введён А. Д. Александровым. Изучение заряда послужило толчком для развития конечно-аддитивной теории меры (40-ые года XX века).
См. также
- Теорема Хана о разложении (англ.)
Литература
- Данфорд Н., Шварц Дж. Линейные операторы. Общая теория. — М.: ИЛ, 1962
- Ландкоф Н. С. Основы современной теории потенциалов. — М., 1966
- Халмош П. Теория меры. / Пер. с англ. — М., 1953.
- Alexandroff A. D. Additive set-functions in abstract spaces I// Матем. сборник 1940. V.8(50), N 2. P.307-348
- Alexandroff A. D. Additive set-functions in abstract spaces II// Матем. сборник 1941. V.9(51), N 3. P.563-628
- Alexandroff A. D. Additive set-functions in abstract spaces III// Матем. сборник 1943. V.13(55), N 2. P.169-293
- Yosida K., Hewitt E. Finitely additive mesures// Trans. Amer. Math. Soc. 1952. v. 72, N 1. P. 46—66
- Положительный заряд
Wikimedia Foundation. 2010.
