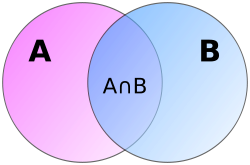
Пересечение множеств

Пересечение $A$ и $B$

Пересече́ние мно́жеств в теории множеств — это множество, которому принадлежат те и только те элементы, которые одновременно принадлежат всем данным множествам.

Определение

Пусть даны два множества $A$ и $B$. Тогда их пересечением называется множество

$A \cap B = \{x \mid x\in A \wedge x \in B\}.$

Замечание

Гораздо реже используется обозначение $AB$.

Свойства

• Пересечение множеств является бинарной операцией на произвольном булеане $2^X$;
• Операция пересечения множеств коммутативна:

  $A \cap B = B \cap A;$

• Операция пересечения множеств ассоциативна:

  $(A\cap B) \cap C = A \cap (B \cap C);$

• Операция пересечения множеств дистрибутивна относительно операции объединения:^[1]

  $\left( \bigcup_k A_k \right) \cap B = \bigcup_k \left( A_k \cap B\right)$

• Универсальное множество $U$ является нейтральным элементом операции пересечения множеств:

  $A\cap U = A;$

• Таким образом булеан вместе с операцией пересечения множеств является абелевой группой;
• Операция пересечения множеств идемпотентна:

  $A \cap A = A;$

• Если $\varnothing$ — пустое множество, то

  $A \cap \varnothing = \varnothing.$

Пример

Пусть $A = \{1,\;2,\;3,\;4\},\;B = \{3,\;4,\;5,\;6\}.$ Тогда

$A \cap B = \{3,\;4\}.$

Примечания

1. ↑ В. А. Ильин, В. А. Садовничий, Бл. Х. Сендов. Глава 2. Вещественные числа // Математический анализ / Под ред. А. Н. Тихонова. — 3-е изд., перераб. и доп. — М.: Проспект, 2006. — Т. 1. — С. 66. — 672 с. — ISBN 5-482-00445-7

См. также

• Операции над множествами