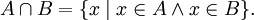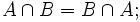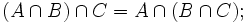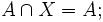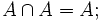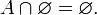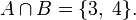Пересечение (теория множеств)
- Пересечение (теория множеств)
-

Пересечение A и B
Пересече́ние мно́жеств в теории множеств — это множество, состоящее из элементов, которые принадлежат одновременно всем данным множествам.
Определение
Пусть даны два множества A и B. Тогда их пересечением называется множество
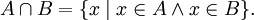
Замечание
Гораздо реже используется обозначение AB.
Свойства
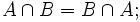
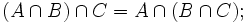
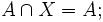
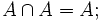
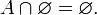
Пример
Пусть 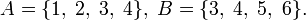 Тогда
Тогда
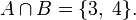
См. также
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое "Пересечение (теория множеств)" в других словарях:
Теория множеств — Теория множеств раздел математики, в котором изучаются общие свойства множеств. Теория множеств лежит в основе большинства математических дисциплин; она оказала глубокое влияние на понимание предмета самой… … Википедия
Пересечение Классов (Множеств) — а логическая операнция по нахождению общих для класса (множества) элементов. Так, П. к. студентов (A) и спортсменов (В) будет класс тех студентов, которые одновременно являются спортсменами. Результат может быть представлен в виде двух… … Словарь терминов логики
АКСИОМАТИЧЕСКАЯ ТЕОРИЯ МНОЖЕСТВ — направление в математич. логике, занимающееся изучением фрагментов содержательной теории множеств методами математич. логики. Обычно с этой целью фрагменты теории множеств оформляются в виде формальной аксиоматич. теории. В более узком смысле… … Математическая энциклопедия
ДЕСКРИПТИВНАЯ ТЕОРИЯ МНОЖЕСТВ — раздел теории множеств, изучающий внутреннее строение множеств в зависимости ют тех операций, при помощи к рых эти множества могут быть построены из множеств сравнительно простой природы (напр., замкнутых или открытых подмножеств данного… … Математическая энциклопедия
Наивная теория множеств — Теория множеств раздел математики, в котором изучаются общие свойства множеств. Теория множеств лежит в основе большинства математических дисциплин; она оказала глубокое влияние на понимание предмета самой математики. Содержание 1 Теория… … Википедия
Описательная теория множеств — Теория множеств раздел математики, в котором изучаются общие свойства множеств. Теория множеств лежит в основе большинства математических дисциплин; она оказала глубокое влияние на понимание предмета самой математики. Содержание 1 Теория… … Википедия
Алгебра (теория множеств) — У этого термина существуют и другие значения, см. Алгебра (значения). Алгебра множеств в теории множеств это непустая система подмножеств, замкнутая относительно операций дополнения (разности) и объединения (суммы). Содержание 1 Определение … Википедия
Полукольцо (теория множеств) — Полукольцо (в теории множеств) система множеств S, для которой выполнены следующие условия: ; ; . Таким образом, полукольцо содержит в себе пустое множество, замкнуто относительно пересечения … Википедия
Кольцо (теория множеств) — У этого термина существуют и другие значения, см. Кольцо. В теории множеств кольцом называют непустую систему множеств R, замкнутую относительно пересечения и симметрической разности конечного числа элементов. Это значит, что для любых элементов… … Википедия
Решётка (теория множеств) — У этого термина существуют и другие значения, см. Решётка. Решётка (ранее использовался термин структура) частично упорядоченное множество, в котором каждое двухэлементное подмножество имеет как точную верхнюю (sup), так и точную нижнюю… … Википедия
 Пересечение A и B
Пересечение A и B — пустое множество, то
— пустое множество, то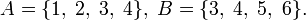 Тогда
Тогда