Тождество Эйлера (комплексный анализ)

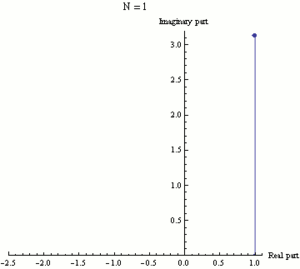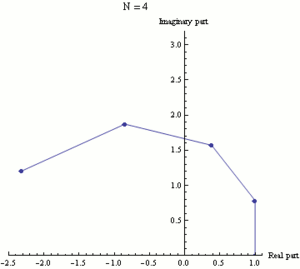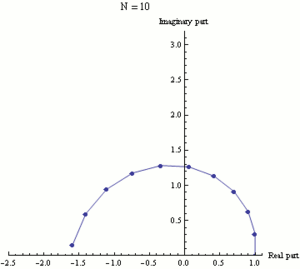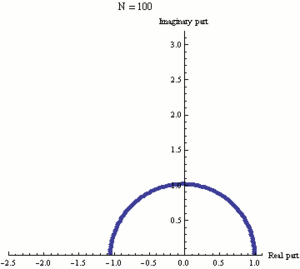Экспоненциальная функция e^z может быть определена как предел последовательности (1 + z/N)^N, при N стремящемуся к бесконечности, и поэтому e^iπ есть предел (1 + iπ/N)^N. На этой анимации N принимает различные возрастающие значения от 1 до 100.

Тождество Эйлера — известное тождество, связывающее пять фундаментальных математических констант:

$e^{i \pi} + 1 = 0, \,\!$

где

$e\,\!$ — число е, или основание натурального логарифма,

$i\,\!$ — мнимая единица,

$\pi\,\!$ — пи, отношение длины окружности к длине ее диаметра,

$1\,\!$ — единица, нейтральный элемент по операции умножения,

$0\,\!$ — ноль, нейтральный элемент по операции сложения.

Тождество Эйлера иногда называют уравнением Эйлера.

История

Формула Эйлера, из которой сразу следует данное тождество, была опубликовано Эйлером в 1740 году. Тождество произвело глубокое впечатление на научный мир. Были даже попытки мистически истолковать его как символ единства математики: числа 0 и 1 относятся к арифметике, мнимая единица — к алгебре, число $\pi$ — к геометрии, а число e — к математическому анализу^[1].

Вывод

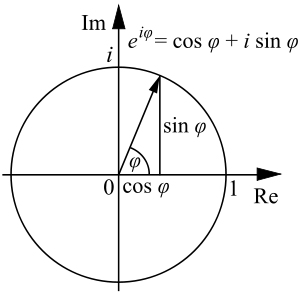
Тождество Эйлера — это особый случай формулы Эйлера из комплексного анализа:

$e^{ix} = \cos x + i \sin x \,\!$

для любого вещественного $x$. (Заметим, что аргументы тригонометрических функций $\sin$ и $\cos$ взяты в радианах). В частности

$e^{i \pi} = \cos \pi + i \sin \pi.\,\!$

А из того, что

$\cos \pi = -1 \, \!$

и

$\sin \pi = 0,\,\!$

следует

$e^{i \pi} = -1,\,\!$

что дает тождество:

$e^{i \pi} +1 = 0.\,\!$

Примечания

1. ↑ Данциг, Тобиас. Числа - язык науки. — М.: Техносфера, 2008. — С. 111. — ISBN 978-5-94836-172-7