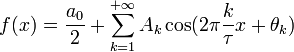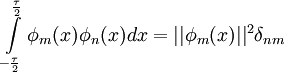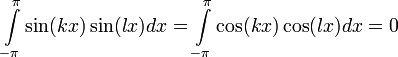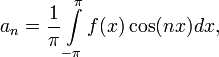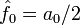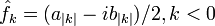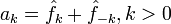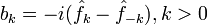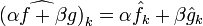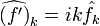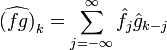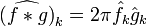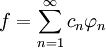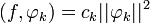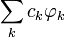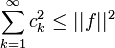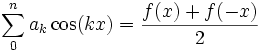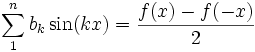- Фурье ряд
-
Ряд Фурье — представление произвольной функции f с периодом τ в виде ряда
Этот ряд может быть также переписан в виде
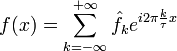 .
.
где
- Ak — амплитуда k-го гармонического колебания (функции cos),
 — круговая частота гармонического колебания,
— круговая частота гармонического колебания,- θk - начальная фаза k-го колебания,
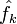 - k-я комплексная амплитуда
- k-я комплексная амплитуда
В более общем виде рядом Фурье элемента гильбертова пространства называется разложение этого элемента по ортогональному базису. Существует множество систем ортогональных функций: Уолша, Лагера, Котельникова...
Разложение функции в ряд Фурье является мощным инструментом при решении самых разных задач благодаря тому, что ряд Фурье прозрачным образом ведёт себя при дифференцировании, интегрировании, сдвиге функции по аргументу и свёртке функций.
Содержание
Тригонометрический ряд Фурье
Неформальное обсуждение
Вектор в евклидовом пространстве можно разложить по ортонормированному базису. При этом многие действия с этим вектором станут намного проще. Функции, заданные на некотором замкнутом ограниченном промежутке, во многом аналогичны векторам — они также образуют линейное пространство, их можно складывать и умножать на числа. Не можем ли мы определить и в этом случае аналогичную процедуру разложения по базису?
Ответ: можем. Для этого необходимо определить наше пространство функций, задать на этом пространстве скалярное произведение и зафиксировать базис, по которому мы будем раскладывать. Наиболее удобные и естественные (для большинства случаев) определение скалярного произведения и выбор базиса приводят к тригонометрическому ряду Фурье.
Скалярное произведение и ортогональность
Пусть φn, φm — две функции пространства
![L^2[-\frac{\tau}{2},\frac{\tau}{2}]](/pictures/wiki/files/51/3232e4fed21c3bc51d66c228d612308e.png) . Определим их скалярное произведение
. Определим их скалярное произведениеУсловие ортогональности
где δnm - дельта Кронекера. Таким образом, скалярное произведение ортогональных функций равно квадрату нормы функции при n = m или нулю в противном случае.
Следующее наблюдение является ключевым в теории рядов Фурье: функции вида sin(kx), cos(kx) попарно ортогональны относительно этого скалярного произведения, то есть при всех целых неотрицательных
 :
:и при всех целых неотрицательных k, l
 .
.
Еще одно важное свойство состоит в том, что тригонометрическая система функций является базисом в пространстве L2[0,2π]. Иными словами, если некоторая функция из этого пространства ортогональна всем функциям вида
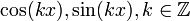 , то она тождественно равна нулю (если точнее, то равна нулю почти всюду).
, то она тождественно равна нулю (если точнее, то равна нулю почти всюду).Классическое определение
Тригонометрическим рядом Фурье функции
![f\in L_2([-\pi,\pi])](/pictures/wiki/files/51/3619025a9e33eaa95a17b18dc1d1256c.png) называют функциональный ряд вида
называют функциональный ряд вида(1) где
Числа a0, an и bn (
 ) называются коэффициентами Фурье функции f. Формулы для них можно объяснить следующим образом. Предположим, мы хотим представить функцию
) называются коэффициентами Фурье функции f. Формулы для них можно объяснить следующим образом. Предположим, мы хотим представить функцию ![f\in L_2([0,2\pi])](/pictures/wiki/files/97/a47d1c775fa95862b8751ccfa3b59eef.png) в виде ряда (1), и нам надо определить неизвестные коэффициенты a0, an и bn. Если умножить правую часть (1) на cos(kx) и проинтегрировать по промежутку [ − π,π], благодаря ортогональности в правой части все слагаемые обратятся в нуль, кроме одного. Из полученного равенства легко выражается коэффициент ak. Аналогично для bk
в виде ряда (1), и нам надо определить неизвестные коэффициенты a0, an и bn. Если умножить правую часть (1) на cos(kx) и проинтегрировать по промежутку [ − π,π], благодаря ортогональности в правой части все слагаемые обратятся в нуль, кроме одного. Из полученного равенства легко выражается коэффициент ak. Аналогично для bkРяд (1) сходится к функции f в пространстве L2([ − π,π]). Иными словами, если обозначить через Sk(x) частичные суммы ряда (1):
 ,
,
то их среднеквадратичное отклонение от функции f будет стремиться к нулю:
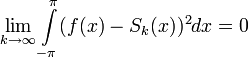 .
.
Несмотря на среднеквадратичную сходимость, ряд Фурье функции, вообще говоря, не обязан сходиться к ней поточечно(см.ниже).
Комплексная запись
Часто при работе с рядами Фурье бывает удобнее в качестве базиса использовать вместо синусов и косинусов экспоненты мнимого аргумента. Мы рассматриваем пространство
![L^2([-\pi,\pi],\mathbb{C})](/pictures/wiki/files/48/0dd98a289dac55d3200b69a873ba0d37.png) комплекснозначных функций со скалярным произведением
комплекснозначных функций со скалярным произведением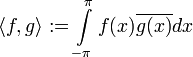 .
.
Мы также рассматриваем систему функций
-
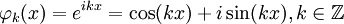 .
.
Как и прежде, эти функции являются попарно ортогональными и образуют полную систему, и, таким образом, любая функция
![f\in L^2([-\pi,\pi],\mathbb{C})](/pictures/wiki/files/98/b0bb7e2d24447b65c09137608c201cea.png) может быть разложена по ним в ряд Фурье:
может быть разложена по ним в ряд Фурье: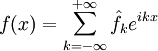 ,
,
где ряд в правой части сходится к f по норме в
![f\in L^2([-\pi,\pi],\mathbb{C})](/pictures/wiki/files/98/b0bb7e2d24447b65c09137608c201cea.png) . Здесь
. Здесь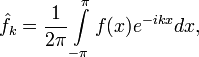 .
.
Коэффициенты :
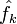 связаны с классическими коэффициентами Фурье по следующим формулам:
связаны с классическими коэффициентами Фурье по следующим формулам:- Комплексная функция вещественной переменной раскладывается в такой же ряд Фурье по мнимым экспонентам, как и вещественная, но, в отличие от последней, для ее разложения
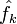 и
и 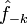 не будут, вообще говоря, комплексно сопряженными.
не будут, вообще говоря, комплексно сопряженными.
Свойства тригонометрического ряда Фурье
Все утверждения этого параграфа верны в предположении, что участвующие в них функции (и результаты операций с ними) лежат в пространстве
![L^2([-\pi,\pi],\mathbb{C})](/pictures/wiki/files/48/0dd98a289dac55d3200b69a873ba0d37.png) .
.- Вычисление коэффициентов Фурье является линейной операцией:
- Справедливо равенство Парсеваля:
-
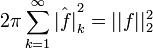 .
.
- Коэффициенты Фурье производной легко выражаются через коэффициенты Фурье самой функции:
- коэффициенты Фурье произведения двух функций выражаются сверткой коэффициентов Фурье сомножителей:
- рассмотрим операцию свертки функций:
где функции предполагаются периодически продолженными с промежутка [ − π,π] на всю прямую. Тогда
Обобщения
Ряды Фурье в гильбертовом пространстве
Описанную выше конструкцию можно обобщить со случая пространства L2[ − π,π] с тригонометрической системой на произвольное гильбертово пространство. Пусть даны ортогональная система
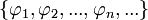 в гильбертовом пространстве R и f — произвольный элемент из R. Предположим, мы хотим представить f в виде (бесконечной) линейной комбинации элементов
в гильбертовом пространстве R и f — произвольный элемент из R. Предположим, мы хотим представить f в виде (бесконечной) линейной комбинации элементов 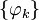 :
:Домножим это выражение на
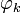 . С учётом ортогональности системы функций
. С учётом ортогональности системы функций 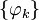 все слагаемые ряда обращаются в ноль, кроме слагаемого при n = k:
все слагаемые ряда обращаются в ноль, кроме слагаемого при n = k:Последовательность чисел
называется координатами, или коэффициентами Фурье элемента f по системе
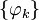 , а ряд
, а рядназывается рядом Фурье элемента f по ортогональной системе
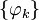 .
.Ряд Фурье любого элемента f по любой ортогональной системе сходится в пространстве R, но его сумма не обязательно равна f. Для ортонормированной системы
 в сепарабельном гильбертовом пространстве следующие условия эквивалентны:
в сепарабельном гильбертовом пространстве следующие условия эквивалентны:- система является базисом, то есть сумма ряда Фурье любого элемента равна этому элементу.
- система является полной, то есть в R не существует ненулевого элемента, ортогонального всем элементам
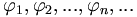 одновременно.
одновременно. - система является замкнутой, то есть для любого
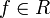 выполнено равенство Парсеваля
выполнено равенство Парсеваля
-
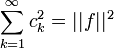 .
.
- линейные комбинации элементов
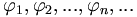 плотны в пространстве R.
плотны в пространстве R.
Если эти условия не выполняются, то сумма ряда Фурье элемента f равна его ортогональной проекции на замыкание линейной оболочки элементов
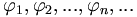 . В этом случае вместо равенства Парсеваля справедливо неравенство Бесселя:Примеры
. В этом случае вместо равенства Парсеваля справедливо неравенство Бесселя:ПримерыТригонометрические функции sin(kx), cos(kx) образуют базис гильбертова пространства L2[ − π,π]. Если мы рассмотрим только косинусы или только синусы, то такая система больше не будет полной. Замыкание линейной обоблочки функций cos(kx) - это все четные функции из L2, а замыкание линейной оболочки функций sin(kx) - все нечетные функции. Результатом разложения функции f в ряды Фурье по этим системам будут соответственно четная и нечетная части функции f:
Еще более интересная ситуация возникает при рассмотрении системы
 . Эта система вновь не будет полной. Замыкание ее линейной оболочки — пространство Харди H2. Элементы этого пространства -- те и только те функции
. Эта система вновь не будет полной. Замыкание ее линейной оболочки — пространство Харди H2. Элементы этого пространства -- те и только те функции 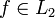 , что f(t) = g(eit), где g — граничные значения некоторой функции, аналитической в круге | z | < 1
, что f(t) = g(eit), где g — граничные значения некоторой функции, аналитической в круге | z | < 1Двойственность Понтрягина
При обобщении теории рядов Фурье на случай гильбертовых пространств теряются свойства, выражающие связь рядов Фурье со сверткой — то, что коэффициенты Фурье свертки функций являются почленными произведениями их коэффициентов Фурье, и наоборот, коэффициенты Фурье произведения представляются сверткой коэффициентов Фурье сомножителей. Эти свойства являются ключевыми для приложений теории Фурье к решению дифференциальных, интегральных и других функциональных уравнений. Поэтому большой интерес представляет такие обобщения теории рядов Фурье, при которых эти свойства сохраняются. Таким обобщением является теория двойственности Понтрягина. Она рассматривает функции, заданные на локально-компактных абелевых группах. Аналогом ряда Фурье такой функции будет функция, заданная на двойственной группе.
Сходимость ряда Фурье
 Сходимость ряда Фурье
Сходимость ряда ФурьеОбзор результатов о сходимости ряда Фурье
Обозначим через SN(f,x) частичные суммы ряда Фурье функции f(x):
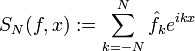 .
.
Далее обсуждается сходимость последовательности функций SN(f,x) к функции f(x) в различных смыслах. Функция f предполагается 2π-периодической (если она задана только на промежутке [ − π,π], ее можно периодически продолжить).
- Если
![f\in L_2([-\pi,\pi])](/pictures/wiki/files/51/3619025a9e33eaa95a17b18dc1d1256c.png) , то последовательность SN(f,x) сходится к функции f(x) в смысле L2. Кроме того, SN(f,x) являются наилучшим (в смысле расстояния в L2) приближением функции f тригонометрическим многочленом степени не выше N.
, то последовательность SN(f,x) сходится к функции f(x) в смысле L2. Кроме того, SN(f,x) являются наилучшим (в смысле расстояния в L2) приближением функции f тригонометрическим многочленом степени не выше N. - Сходимость ряда Фурье в заданной точке x0 — локальное свойство, то есть, если функции f и g совпадают в некоторой окрестности x0, то последовательности SN(f,x0) и SN(g,x0) либо одновременно расходятся, либо одновременно сходятся, и в этом случае их пределы совпадают.
- Если функция f дифференцируема в точке x0, то ее ряд Фурье в этой точке сходится к f(x0). Более точные достаточные условия в терминах гладкости функции f задаются признаком Дини.
- Функция, непрерывная в точке x0, может иметь расходящийся в ней ряд Фурье. Однако, если он сходится, то непременно к f(x0). Это следует из того, что для непрерывной в x0 функции f последовательность SN(f,x0) сходится по Чезаро к f(x0).
- Если функция f разрывна в точке x0, но имеет пределы в этой точке справа и слева
 , то при некоторых дополнительных условиях SN(f,x0) сходятся к (f(x0 + 0) + f(x0 − 0)) / 2. Подробнее см. модифицированный признак Дини.
, то при некоторых дополнительных условиях SN(f,x0) сходятся к (f(x0 + 0) + f(x0 − 0)) / 2. Подробнее см. модифицированный признак Дини. - Теорема Карлесона: если
![f\in L_2([-\pi,\pi])](/pictures/wiki/files/51/3619025a9e33eaa95a17b18dc1d1256c.png) , то ее ряд Фурье сходится к ней почти всюду. Это верно и если
, то ее ряд Фурье сходится к ней почти всюду. Это верно и если ![f\in L_p([-\pi,\pi]), p&amp;gt;1](/pictures/wiki/files/97/a99b78095fbc4944de36d6827ebe948e.png) . Однако, существуют функции из L1([ − π,π]), ряд Фурье которых расходится во всех точках.
. Однако, существуют функции из L1([ − π,π]), ряд Фурье которых расходится во всех точках. - Зафиксируем точку
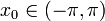 . Тогда множество всех непрерывных функций, ряд Фурье которых сходится в этой точке, является множеством первой категории в пространстве C([ − π,π]). В некотором смысле это означает, что «типичная» непрерывная функция имеет расходящийся ряд Фурье.
. Тогда множество всех непрерывных функций, ряд Фурье которых сходится в этой точке, является множеством первой категории в пространстве C([ − π,π]). В некотором смысле это означает, что «типичная» непрерывная функция имеет расходящийся ряд Фурье.
Убывание коэффициентов Фурье и регулярность функции
Существует фундаментальная связь между регулярностью (интегрируемостью, непрерывностью, гладкостью) функции и скоростью убывания ее коэффициентов Фурье. Чем «лучше» функция, тем быстрее ее коэффициенты стремятся к нулю, и наоборот. Степенное убывание коэффициентов Фурье присуще функциям класса C(k), а экспоненциальное — аналитическим функциям. Примеры такого рода связи:
- Коэффициенты Фурье любой интегрируемой функции стремятся к нулю (Теорема Римана-Лебега).
- Если функция f принадлежит классу C(k)([ − π,π]), то есть дифференцируема k раз и ее k-я производная непрерывна, то

- Если ряд
 сходится абсолютно, то
сходится абсолютно, то ![f\in C^{(k)}([-\pi,\pi])](/pictures/wiki/files/54/6be331206edc391c383e3522068aecd0.png) при всех k < α.
при всех k < α. - Если функция принадлежит классу Гельдера с показателем α > 1 / 2, то ряд
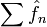 сходится абсолютно (Теорема Бернштейна).
сходится абсолютно (Теорема Бернштейна). - Если
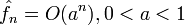 , то функция f является аналитической. Верно и обратное.
, то функция f является аналитической. Верно и обратное.
См. также
- Преобразование Фурье
- Быстрое преобразование Фурье
- Признак Жордана
- Признак Дини
- Числовой ряд
- АТС теорема
Примечания
Литература
- Жук В.В., Натансон Г.И. Тригонометрические ряды Фурье и элементы теории аппроксимации. — Л.: Изд-во Ленингр. ун-та, 1983. — С. 188.
- Рудин У. Основы математического анализа. — 1976.
- Пискунов Н.С. Дифференциальное и интегральное исчисления для ВТУЗов. — М.: «Наука», 1964. — Т. 2.
Wikimedia Foundation. 2010.