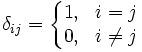Дельта Кронекера

Символ Кронекера (или 'дельта Кронекера) — функция двух переменных, которая равна 1, если они равны, и 0 в противном случае. Переменные обычно предполагаются целыми.

$\delta_{ij} = \left\{\begin{matrix} 1, & i=j \\ 0, & i \ne j \end{matrix}\right.$

Например, 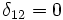$\delta_{12} = 0 \$, но $\delta_{33} = 1 \$.

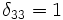Т.е. матрица составленная из элементов (δ_ij) является единичной.

Символ Кронекера обычно трактуется скорее как тензорное обозначение. В частности, различные написания δ_ij, δ^ij и 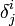$\delta^i_j$ используются чтоб подчеркнуть принадлежность к определённому типу тензоров; соответственно дважды ковариантным, один раз ковариантным и один контравариантным и дважды контравариантным.

Символ Кронекера используется для записи условия ортонормированности базиса (e_i,e_j) = δ_ij, где круглыми скобками обозначено скалярное произведение.

Замечание: обычная практика обозначать той же буквой тензор после поднятия или опускания индекса не распространяется на дельту Кронекера! Это верно только в ортонормированных базисах, и, собственно говоря, является признаком, выделяющим ортонормированные базисы из всех.

История

Функция была введена Кронекером в 1866.

Примечания

См. также

• Символ Леви-Чивиты
• Дельта-функция Дирака