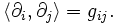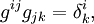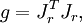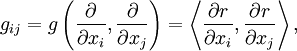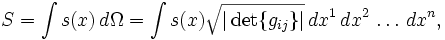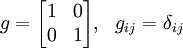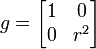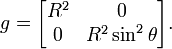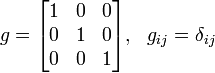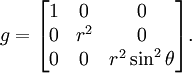Основной тензор

Метрический тензор или метрика — это симметричный тензор ранга 2 на гладком многообразии, посредством которого задаются скалярное произведение векторов в касательном пространстве, длины кривых, углы между кривыми и т. д.

В частном случае поверхности, метрика также называется первой квадратичной формой.

В общей теории относительности метрика рассматривается в качестве фундаментального физического поля (гравитационного) на четырехмерном многообразии физического пространства-времени. Широко используется и в других построениях теоретической физики, в частности, в биметрической теории гравитации на пространстве-времени рассматривают сразу две метрики.

• (Далее в формулах этой статьи с повторяющимися индексами везде подразумевается суммирование по правилу Эйнштейна, то есть по каждому повторяющемуся индексу).

Способы задания

Координатное представление

Метрический тензор в локальных координатах 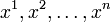$x^1,x^2,\dots,x^n$, обычно задаётся как ковариантное тензорное поле 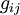$g_{ij}\$. Через него определяются скалярные произведения координатных векторных полей $\partial_i=\frac{\partial}{\partial x^i}$:

$\left\langle\partial_i,\partial_j\right\rangle=g_{ij}.$

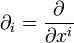А для любых векторных полей, скалярное произведение вычисляется по формуле

$\left\langle v,w\right\rangle=g_{ij}v^iw^j$,

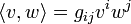где 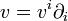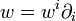$v=v^i\partial_i$, $w=w^i\partial_i$ — представление векторных полей в локальных координатах.

Замечания

Иногда метрический тензор задаётся двойственным способом, с помощью контравариантного тензора g^ij. В случае невырожденных метрик

$g^{ij}g_{jk}=\delta^i_k,$

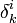где $\delta^i_k$ — символ Кронекера.

Так, оба способа эквивалентны, но оба представления метрики бывают полезны. Для вырожденных метрик иногда удобнее пользоваться именно контравариантной метрикой. Например, субриманова метрика может быть определена через тензор g^ij, но тензор g_ij для неё неопределён.

Представление в поле реперов

Иногда удобно задавать метрический тензор через выбранное (не обязательно координатное, как это описано выше) поле реперов. То есть выбором реперного поля 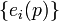$~\{e_i(p)\}$ и матрицы $g_{ik}(p) = \langle e_i(p), e_k(p)\rangle$.

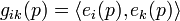Например, риманов метрический тензор может быть задан ортонормированным полем реперов^[1].

Индуцированная метрика

Метрика, которая индуцируется гладким вложением r многообразия M в евклидово пространство E, может быть посчитана по формуле:

$g = J_r^T J_r,$

где J_r означает матрицу Якоби вложения r и 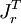$J^T_r$ — транспонированная к ней. Иначе говоря, скалярные произведения базисных координатных векторов касательного пространства 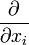$\frac{\partial}{\partial x_i}$ определяются как

$g_{ij}=g\left(\frac\partial{\partial x_i},\frac\partial{\partial x_j}\right)= \left\langle\frac{\partial r}{\partial x_i},\frac{\partial r}{\partial x_j}\right\rangle,$

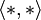где $\langle*,*\rangle$ обозначает скалярное произведение в E.

Более общо

Пусть (N,h) многообразие с метрикой и 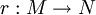$r:M\to N$ гладкое вложение. Тогда метрика g на M, определённая равенством

g(X,Y) = h(dr(X),dr(Y))

называется индуцированной метрикой. Здесь dr обозначает дифференциал отображения r.

Типы метрических тензоров

Множество метрических тензоров g подразделяется на два класса:

• невырожденные или псевдоримановы метрики, когда 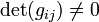$\ \det(g_{ij}) \neq 0$ во всех точках многообразия. Среди невырожденных метрических тензоров, в свою очередь, различаются
  • риманов метрический тензор (или риманова метрика) для которого квадратичная форма является положительно определенной. Многообразие с выделенным римановым метрическим тензором называется римановым, они имеют естественную структуру метрического пространства.
  • собственно псевдориманов метрический тензор (или индефинитная метрика), когда форма не является положительно определенной. Многообразие с выделенным псевдориамоновым метрическим тензором называется (собственно) псевдоримановым.
    • В частности метрика Лоренца.
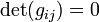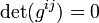• вырожденные, когда $\ \det(g_{ij}) = 0$ либо $\ \det(g^{ij}) = 0$ в некоторых точках.
  • Многообразие 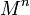$M^n\$, метрика которого является вырожденной в любой точке, называется изотропным (например, световой конус в пространстве Минковского).
  • Субримановы метрики.

Обычно под метрическим тензором без специального на то указания понимается риманов метрический тензор; но если, рассматривая невырожденный метрический тензор, хотят подчеркнуть, что речь идет именно о римановом, а не псевдоримановом метрический тензоре, то о нём говорят как о собственно римановом метрическом тензоре.

Иногда под псевдоримановым тензором и псевдоримановым многообразием понимают то, что выше определено как собственно псевдоримановы метрика и многообразие, а для первых сохраняется только термин «невырожденная метрика» и соответственно «многообразие с невырожденной метрикой».

Связанные определения

• Вектор нулевой длины в пространстве с псевдоримановой метрикой называется изотропным (также нулевым или светоподобным) и задает определенное изотропное направление на многообразии; например, свет в пространственно-временном континууме путешествует вдоль изотропных направлений.
• Многообразие с выделенным римановым метрическим тензором называется риманово многообразие
• Многообразие с выделенным псевдоримановым метрическим тензором называется псевдориманово многообразие

Свойства

• Риманов метрический тензор может быть введен на любом паракомпактном гладком многообразии.

• Риманов метрический тензор индуцирует на многообразии естественную структуру метрического пространства

• Индефинитная метрика не порождает метрического пространства. Однако на ее основе может быть, по крайней мере в некоторых случаях, специальным образом построена топология (см. Топология Александрова), вообще говоря, не совпадающая с естественной топологией многообразия.

Метрика и объём

Определитель матрицы метрического тензора | det{g_ij} | дает квадрат объема параллелепипеда, натянутого на базисные векторы. (В ортонормированных базисах это единица).

Поэтому величина 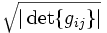$\sqrt{|\det \{g_{ij}\}|}$ играет важную роль при вычислении объемов, а также при интегрировании по объему. В частности, 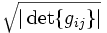$\sqrt{|\det \{g_{ij}\}|}$ входит в общее выражение тензора Леви-Чивиты, используемого для вычисления смешанного произведения, векторного произведения и их многомерных аналогов.

Интегрирование же по объему включает этот множитель, например, при необходимости проинтегрировать в координатах какой-то скаляр (чтобы результат был инвариантным):

$S = \int s(x)\,d\Omega = \int s(x) \sqrt{|\det \{g_{ij}\}|}\,dx^1\,dx^2\,\ldots\,dx^n,$

где dΩ — это элемент n-мерного объема, а dxⁱ — дифференциалы координат.

• Для подмногообразий объём (площадь) определяется как объём (площадь) относительно индуцированной метрики.

Примеры

• Метрический тензор на евклидовой плоскости:
  • В прямоугольных декартовых координатах единичного масштаба метрический тензор постоянен (не зависит от координат) и представлен единичной матрицей (его компоненты равны символу Кронекера)

    $g = \begin{bmatrix} 1 & 0 \\ 0 & 1\end{bmatrix},\ \ g_{ij}=\delta_{ij}$

  • В прямоугольных декартовых координатах неединичного масштаба метрический тензор представлен постоянной (не зависящей от координат) диагональной матрицей, ненулевые компоненты которой определяются масштабом по каждой оси (вообще говоря они не равны).
  • В косоугольных декартовых координатах метрический тензор постоянен (не зависит от координат) и положительно определён, но в остальном, вообще говоря, представлен произвольной симметричной матрицей.
  • В полярных координатах: (r,θ)

    $g = \begin{bmatrix} 1 & 0 \\ 0 & r^2\end{bmatrix} \$

• Метрический тензор на сфере. Сфера (двумерная) радиуса R, вложенная в трехмерное пространство, имеет естественную метрику, индуцированную евклидовой метрикой объемлющего пространства. В стандартных сферических коордиранах 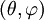$(\theta,\varphi)$ метрика принимает вид:

  $g = \begin{bmatrix} R^2 & 0 \\ 0 & R^2 \sin^2 \theta\end{bmatrix}.$

• Метрический тензор для трехмерного евклидова пространства:
  • В прямоугольных декартовых координатах единичного масштаба метрический тензор постоянен (не зависит от координат) и представлен единичной матрицей (его компоненты равны символу Кронекера)

    $g = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{bmatrix},\ \ g_{ij}=\delta_{ij}$

  • В прямоугольных декартовых координатах неединичного масштаба метрический тензор представлен постоянной (не зависящей от координат) диагональной матрицей, ненулевые компоненты которой определяются масштабом по каждой оси (вообще говоря они не равны).
  • В косоугольных декартовых координатах метрический тензор постоянен (не зависит от координат) и положительно определён, но в остальном, вообще говоря, представлен произвольной симметричной матрицей.
  • В сферических координатах: (r,θ,φ):

    $g = \begin{bmatrix} 1 & 0 & 0 \\ 0 & r^2 & 0 \\ 0 & 0 & r^2 \sin^2 \theta\end{bmatrix}.$

• Метрика Лоренца (Метрика Минковского).
• Метрика Шварцшильда

Изоморфизм между касательным и кокасательным пространством

Метрический тензор устанавливает изоморфизм между касательным пространством и кокасательным пространством: пусть 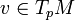$v \in T_p M$ — вектор из касательного пространства, тогда для метрического тензора g на M, мы получаем, что 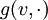$g(v,\cdot)$, то есть отображение, которое переводит другой вектор 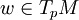$w \in T_p M$ в число g(v,w), является элементом дуального пространства линейных функционалов (1-форм) 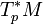$T_p^*M$. Невырожденность метрического тензора превращает это отображение в биекцию, а тот факт, что g сам по себе есть тензор, делает это отображение независимым от координат.

Для тензорных полей, это позволяет «поднимать и опускать индексы» у любого тензорного поля (жаргонное название — «жонглирование индексами»). В компонентах операция поднятия-опускания индекса, выглядит так:

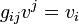$\ g_{ij}v^j = v_i$ — опускание индекса для вектора,

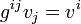$\ g^{ij}v_j = v^i$ — поднятие индекса для вектора,

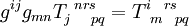$\ g^{ij}g_{mn}T_{j\ \ \ pq}^{\ nrs} = T_{\ m\ \ pq}^{i\ \ rs}$ — пример одновременного поднятия индекса j и опускания индекса n для тензора большой валентности.

(К скалярам эта операция, естественно, не применяется).

Для тензороподобных объектов (не являющихся тензорами), как символы Кристоффеля, преобразование контравариантных компонент в ковариантные и обратно определяется, как правило, так же как и для тензорных. При желании жонглирование можно применить и к матрицам Якоби, только в этом случае нужно проследить за тем, что метрика для поднятия-опускания первого индекса будет, конечно, вообще говоря отличаться от метрики для такой же операции со вторым.

Примечания

1. ↑ См. например
   • Картан Э. Ж. Риманова геометрия в ортогональном репере. — М.: изд-во МГУ, [1926-1927]1960
   • Картан Э. Ж. Теория конечных непрерывных групп и дифференциальная геометрия изложенная методом подвижного репера. — М.: изд-во МГУ, [1930]1963

См. также

• Тензор кривизны
• Ковариантная производная
• Метрическое пространство

Ссылки