- МЕТРИЧЕСКИЙ ТЕНЗОР
- МЕТРИЧЕСКИЙ ТЕНЗОР
-
совокупность величин, определяющих геом. свойства пространства (его метрику). В теории относительности М. т. определяет метрику пространства-времени.
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- МЕТРИЧЕСКИЙ ТЕНЗОР
-
- дважды ковариантный симметричный тензор
заданный в области ри манова пространства с координатами 
, причём матрица 
положительно определена: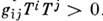
, если вектор 
(принято соглашение о суммировании по повторяющимся индексам). При замене координат 
M. т. 
переходит в 
M. т. иногда наз. римановой метрикой, поскольку он определяет расстояние в ри-мановом пространстве: если задана кривая 
,
то её длина 
а элемент длины ds определён ф-лой
правая часть к-рой наз. первой (основной) квадратичной формой. Элемент объёма 
а объём V(U )области U равен
где
Если существуют координаты 
, в к-рых M. т. имеет вид
где 
- Кронекера символ, то метрика наз. евклидовой, а сама область риманова пространства является областью евклидова пространства.Кроме М. т., в римановом пространстве вводится ещё одна независимая структура - связность, задающая ковариантную производную
M. т. наз. согласованным со связностью, если он ковариантно постоянен:
Тогда коэф. связности, или Кристоффеля символы, однозначно выражаются через M. т.:
В окрестности любой точки
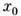можно ввести нормальные (римановы) координаты, такие, что 
или 
Тогда в этой окрестности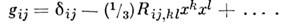 
Коэф.
характеризуют отличие M. т. от евклидова и являются компонентами кривизны тензора. Помимо внутр. характеристик многообразия, M. т. задаёт скалярное произведение векторов 
и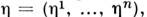 
касательных к многообразию в данной точке: 
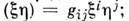скалярное произведение не зависит от выбора системы координат.Понятие M. т. общеупотребительно при описании сплошной среды, при формулировке теории поля в криволинейных координатах, а особенно - в теории относительности и теории тяготения.
Лит.: Ландау Л. Д., Лифшиц E. M., Теория поля, 7 изд., M., 1988; Рашевский П. К., Риманова геометрия и тензорный анализ, 3 изд., M., 1967; Fон В. А., Теория пространства, времени и тяготения, 2 изд., M., 1961; Дубровин Б. А., Новиков С. П., Фоменко А. Т., Современная геометрия, 2 изд., M., 1986. В. П. Павлов.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
