- Касательное пространство
-
Касательное пространство к гладкому многообразию
 в точке
в точке  — совокупность касательных векторов с введённой на ней естественной структурой векторного пространства. Касательное пространство к
— совокупность касательных векторов с введённой на ней естественной структурой векторного пространства. Касательное пространство к  в точке
в точке  обычно обозначается
обычно обозначается  или — когда очевидно, о каком многообразии идёт речь — просто
или — когда очевидно, о каком многообразии идёт речь — просто  .
.Совокупность касательных пространств во всех точках многообразия (вместе с самим многообразием) образует векторное расслоение, которое называется касательным расслоением. Соответственно, каждое касательное пространство есть слой касательного расслоения.
Касательное пространство в точке
 к подмногообразию определяется аналогично.
к подмногообразию определяется аналогично.В простейшем случае, когда гладкое многообразие гладко вложено в векторное пространство (что возможно всегда, согласно Теореме Уитни о вложении), каждое касательное пространство можно естественно отождествить с некоторым афинным подпространством объемлющего векторного пространства.
Содержание
Определения
Есть два стандартных определения касательного пространства: через класс эквивалентости гладких кривых и через дифференцирование в точке. Первое интуитивно проще, но на этом пути возникает ряд технических сложностей. Второе является наиболее простым, хотя уровень абстракции в нём выше. Второе определение также легче применять на практике.
Как класс эквивалентости гладких кривых
Пусть
 — гладкое многообразие и
— гладкое многообразие и  . Рассмотрим класс
. Рассмотрим класс  гладких кривых
гладких кривых  таких, что
таких, что  . Введём на
. Введём на  отношение эквивалентости:
отношение эквивалентости:  если
еслив некоторой (а значит и в любой) карте содержащей
 .
.Элементы касательного пространства
 определяются как
определяются как  -классы эквивалентности
-классы эквивалентности  ; то есть
; то есть .
.
В карте такой, что
 соответствует началу коодинат, кривые из
соответствует началу коодинат, кривые из  можно складывать и умножать на число следующим образом
можно складывать и умножать на число следующим образомПри этом результат остаётся в
 .
.Эти операции продожаются до классов эквивалентности
 . Более того, индуцированные на
. Более того, индуцированные на  операции уже не зависят от выбора карты. Так на
операции уже не зависят от выбора карты. Так на  определяется структура векторного пространства.
определяется структура векторного пространства.Через дифференцирование в точке
Пусть
 —
—  -гладкое многообразие. Тогда касательным к многообразию
-гладкое многообразие. Тогда касательным к многообразию  в точке
в точке  называется пространство дифференцирований в этой точке, то есть пространство операторов
называется пространство дифференцирований в этой точке, то есть пространство операторов  , сопоставляющих каждой гладкой функции
, сопоставляющих каждой гладкой функции  число
число  и обладающих следующими свойствами:
и обладающих следующими свойствами:- аддитивность:

- правило Лейбница:

На множестве всех дифференцирований в точке
 возникает естественная структура линейного пространства:
возникает естественная структура линейного пространства:Замечания
- В случае
 -гладких многообразий, в определении через дифференцирование следует добавить ещё одно свойство
-гладких многообразий, в определении через дифференцирование следует добавить ещё одно свойство
 если
если 
- в некоторой (а значит и в любой) карте содержащей
 .
.
- В противном случае это определение даст бесконечномерное пространство, включающее касательное пространство. Это пространство иногда называется алгебраическим касательным пространством. См. ниже.
- Пусть
 . Тогда правило Лейбница и свойство адитивности для оператора выполняются для
. Тогда правило Лейбница и свойство адитивности для оператора выполняются для  . Это позволяет иденцифицировать касательные пространства получаемые в первом и вторым определении.
. Это позволяет иденцифицировать касательные пространства получаемые в первом и вторым определении.
Свойства
- Касательное пространство
 -мерного гладкого многообразия является
-мерного гладкого многообразия является  -мерным векторным пространством
-мерным векторным пространством - Для выбранной локальной карты
 , операторы
, операторы  дифференцирования по
дифференцирования по  :
:
- представляют собой базис
 , называемый голономным базисом.
, называемый голономным базисом.
Связанные определения
- Контактным элементом к многообразию в некоторой точке называется любая гиперплоскость касательного пространства в этой точке.
Вариации и обобщения
Алгебраическое касательное пространство
Алгебраическое касательное пространство возникает, когда мы в определении касательного вектора отказываемся от дополнительного требования, озвученного в замечании выше (что, впрочем, имеет значение только для
 -дифференцируемых многообразий,
-дифференцируемых многообразий,  ). Оно обобщается на любое локально окольцованное пространство.
). Оно обобщается на любое локально окольцованное пространство.Пусть
 —
—  -дифференцируемое многообразие,
-дифференцируемое многообразие,  — кольцо дифференцируемых функций из
— кольцо дифференцируемых функций из  в
в  . Рассмотрим кольцо
. Рассмотрим кольцо  ростков функций в точке
ростков функций в точке  и каноническую проекцию
и каноническую проекцию ![[-]_x: C^k(M) \to C^k_x](4fa1a28082ff9c7aa3475e0f9f103f03.png) . Обозначим через
. Обозначим через  ядро гомоморфизма колец
ядро гомоморфизма колец ![[f]_x \mapsto f(x)](530c9b510b8dbb4516578284c29efbde.png) . Введем на
. Введем на  структуру вещественной алгебры с помощью инъективного гомоморфизма
структуру вещественной алгебры с помощью инъективного гомоморфизма  ,
, ![i(a) = [\mathrm{const}_a]_x](16d069d7dbdd2685f08db958878f70bf.png) и будем далее отождествлять
и будем далее отождествлять  и
и  . Имеет место равенство
. Имеет место равенство  .[1] Обозначим через
.[1] Обозначим через  подалгебру
подалгебру  , состояющую из всех ростков, представители которых имеют нулевые дифференциалы в точке
, состояющую из всех ростков, представители которых имеют нулевые дифференциалы в точке  в каждой карте; обозначим
в каждой карте; обозначим  . Заметим, что
. Заметим, что  .
.Рассмотрим два векторных пространства:
 — это пространство имеет размерность
— это пространство имеет размерность  и совпадает с определенным ранее касательным пространством к
и совпадает с определенным ранее касательным пространством к  в точке
в точке  ,
, — это пространство изоморфно пространству дифференцирований
— это пространство изоморфно пространству дифференцирований  со значениями в
со значениями в  , его называют алгебраическим касательным пространством[2]
, его называют алгебраическим касательным пространством[2]  в точке
в точке  .
.
Если
 , то
, то  имеет размерность континуум, а
имеет размерность континуум, а  содержит
содержит  как нетривиальное подпространство; в случае
как нетривиальное подпространство; в случае  или
или  эти пространства совпадают (и
эти пространства совпадают (и  ).[3] В обоих случаях
).[3] В обоих случаях  можно отождествлять с (под)пространством дифференцирований
можно отождествлять с (под)пространством дифференцирований  со значениями в
со значениями в  , для вектора
, для вектора  формула
формула ![X(f) = X([f]_x)](b31b75632799dd05e90ac9523ac8a02e.png) задает инъективный гомоморфизм
задает инъективный гомоморфизм  в пространство дифференцирований
в пространство дифференцирований  со значениями в
со значениями в  (структура вещественной алгебры на
(структура вещественной алгебры на  задается аналогично
задается аналогично  ). При этом в случае
). При этом в случае  получается в точности определение, данное выше.
получается в точности определение, данное выше.См. также

Примечания
Категория:- Дифференциальная геометрия и топология
Wikimedia Foundation. 2010.

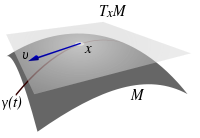
 и касательный вектор
и касательный вектор  , вдоль кривой
, вдоль кривой  , проходящей через точку
, проходящей через точку 





