- НЕЛИНЕЙНАЯ ОПТИКА
- НЕЛИНЕЙНАЯ ОПТИКА
-
раздел оптики, охватывающий исследования распространения мощных световых пучков в тв. телах, жидкостях и газах и их вз-ствия с в-вом. Сильное световое поле изменяет оптич. хар-ки среды (показатель преломления, коэфф. поглощения), к-рые становятся ф-циями напряжённости электрич. поля Е световой волны, т. е. поляризация среды нелинейно зависит от Е. Н. о. имеет много общего с нелинейной теорией колебаний (см. НЕЛИНЕЙНЫЕ СИСТЕМЫ), нелинейной акустикой и др.Историческая справка.Начало совр. этапа в развитии Н. о. (1961) связано с созданием лазеров, к-рое открыло возможности изучения и использования нелинейных явлений фактически во всех областях физ. и прикладной оптики. С появлением лазеров оптика получила источники когерентного излучения большой мощности. С помощью импульсных лазеров можно получить интенсивности света I=107—109 Вт/см2. Мощные лазерные системы позволяют получить I=1016 Вт/см2. Напряжённости светового поля Е (I пропорц. Е2) в таких пучках сравнимы или даже превышают внутриатомные поля. В таких световых нолях возникают новые оптич. эффекты и существенно изменяется характер уже известных явлений.Вместе с тем ясные представления о том, что законы линейной оптики (суперпозиции принцип) носят приближённый характер и применимы лишь для не слишком сильных световых полей, существовали и до появления лазеров. Ок. 50 лет назад С. И. Вавиловым были поставлены эксперименты с целью обнаружения нелинейных явлений. В 1923 Вавилов и В. Л. Лёвшин обнаружили уменьшение поглощения света урановым стеклом с ростом интенсивности света и объяснили это тем, что в сильном эл.-магн. поле большая часть атомов (или молекул) находится в возбуждённом состоянии и уже не может поглощать свет. Считая, что это лишь один из множества возможных оптич. нелинейных эффектов, Вавилов впервые ввёл термин «Н. о.». В 50-х гг. Г. С. Горелик теоретически рассмотрел возможность наблюдения ряда нелинейных оптич. эффектов с помощью фотоэлектрич. умножителей. Один из них — смещение оптич. дублета с выделением разностной частоты, лежащей в диапазоне СВЧ (г е т е р о д и н и р о в а н и е с в ет а),— наблюдали в 1955 А. Форрестер, Р. Гудмундсен и П. Джонсон (США). К Н. о. в широком смысле относятся и хорошо известные электро-оптические эффекты (линейный Поккельса эффект и квадратичный Керра эффект). Оказалось, что влияние низкочастотного электрич. поля на показатель преломления среды имеет ту же физ. природу, что и такие нелинейно-оптич. явления, как генерация оптич. гармоник и смешение частот (си. ниже).В 1961 П. Фрайкен с сотрудниками (США) открыл эффект удвоения частоты света в кристаллах — генерацию 2-й гармоники. В 1962 наблюдалось утроение частоты (генерация 3-й гармоники). В 1961—63 в СССР (Р. В. Хохлов, С. А. Ахманов) и в США (Н. Бломберген) были получены фундаментальные результаты в теории нелинейных оптич. явлений, заложившие теор. основы Н. о. В 1962—63 открыто и объяснено вынужденное комбинационное рассеяние света, что послужило толчком к изучению вынужденного рассеяния др. видов. В 1965 обнаружена самофокусировка света. При этом мощный световой пучок, распространяясь в среде, во многих случаях не испытывает обычной, т. н. дифракционной, расходимости, а, напротив, самопроизвольно сжимается.В 1965 были созданы параметрические генераторы света, в к-рых нелинейные оптич. эффекты используются для генерирования когерентного оптич. излучения, плавно перестраиваемого по частоте в широком диапазоне длин волн l. В 1967 началось исследование нелинейных явлений, связанных с распространением в среде сверхкоротких (длительностью до 10-12 с) световых импульсов. С 1969 развиваются методы нелинейной и активной спектроскопии (см. ниже).Наиболее важные разделы совр. Н. о.: волновая Н. о., исследования нелинейной поляризации среды и нелинейная спектроскопия, прикладная Н. <о.Взаимодействие сильного светового поля со средой.Элем. процесс, лежащий в основе вз-ствия света со средой,— возбуждение атома или молекулы световым полем и переизлучение света возбуждённой ч-цей. Матем. описанием этих процессов явл. ур-ния, связывающие поляризацию Р ед. объёма среды с напряжённостью поля E (м а т е р и а л ь н ы е у р а в н е н и я). Линейная оптика базируется на приближённом соотношении:Р=cЕ, (1)где c — диэлектрическая восприимчивость, зависящая только от св-в среды (см. ДИЭЛЕКТРИКИ). Согласно (1), переизлучённое поле имеет ту же частоту, что и падающее, следовательно, ур-ние (1) не описывает ни возникновения оптич. гармоник, ни др. нелинейные эффекты. Это означает, что соотношением (1) можно пользоваться лишь в области слабых световых полей.Суть приближений, лежащих в основе (1), можно понять, обращаясь к классич. модели осциллятора, используемой для описания вз-ствия света с в-вом. Поведение атома или молекулы в световом поле эквивалентно колебаниям осциллятора. Характер отклика ат. осциллятора на световую волну можно установить, сравнивая E с напряжённостью внутриатомного поля Ea»e/a2»108 —109 В/см (е — заряд эл-на, a — ат. радиус), определяющего силы связи в ат. осцилляторе. В пучках нелазерных источников Е»1—10 В/см, т. е. Е<-Еа, и ат. осциллятор можно считать гармоническим. Прямым следствием этого явл. (1). В пучках мощных лазеров можно получить Е вплоть до 106 —107 В/см, уже сравнимые с Еа. При этом осциллятор становится ангармоническим, нелинейным, что приводит к нелинейной зависимости между поляризацией среды Р и E. При (E/Ea)<1 P можно представить в виде разложения в ряд но параметру Е/Еа:P=c(1)E+c(2)E2+c(3)E3+... (2)Коэфф.c(1), c(2) и т. д. наз. н е л и н е й н ы м и в о с п р и и м ч и в о с т я м и (по порядку величины c(1)= =1/Ea; c(2)=1/E2a. Ур-ние (2) является основой Н. о. Если на поверхность среды падает монохроматич. световая волна Е=Аcos(wt-kx), где А — амплитуда, w — частота, k — волновое число, х — координата точки вдоль направления распространения волны, t — время, то, согласно (2), поляризация среды наряду с линейным членом РЛ =c(1)Acos(wt-kx) содержит ещё и нелинейный член 2-го порядка: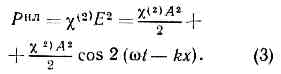 Последнее слагаемое в (3) описывает поляризацию, изменяющуюся с частотой 2w, т. е. генерацию 2-й гармоники. Генерация 3-й гармоники, а также зависимость показателя преломления n от интенсивности описываются членом c(3)E3 в (2) и т. д. (член с c(2) описывает также линейный злектрооптич. эффект, если в (2) представить Е в виде: Е=Е0+Есв, где Е0 — статич. поле, Есв — электрич. поле световой волны, а член с c (3) описывает эффект Керра).Нелинейный отклик ат. или мол. осциллятора на сильное световое поле — наиболее универсальная причина нелинейных оптич. эффектов. Существуют и др. причины: напр., изменение показателя преломления n может быть вызвано нагревом среды лазерным излучением. Изменение темп-ры DT=aЕ2 (a — коэфф. поглощения света) приводит к изменению n от n0 до n=n0+(дn/дT)DT. Во мн. случаях существенным оказывается также эффект электрострикции (сжатие среды в световом поле Е). В сильном световом поле Е лазера электрострикц. давление, пропорц. Е2, изменяет плотность среды, что может привести к генерации звук. волн. С тепловыми эффектами связана самодефокусировка света.
Последнее слагаемое в (3) описывает поляризацию, изменяющуюся с частотой 2w, т. е. генерацию 2-й гармоники. Генерация 3-й гармоники, а также зависимость показателя преломления n от интенсивности описываются членом c(3)E3 в (2) и т. д. (член с c(2) описывает также линейный злектрооптич. эффект, если в (2) представить Е в виде: Е=Е0+Есв, где Е0 — статич. поле, Есв — электрич. поле световой волны, а член с c (3) описывает эффект Керра).Нелинейный отклик ат. или мол. осциллятора на сильное световое поле — наиболее универсальная причина нелинейных оптич. эффектов. Существуют и др. причины: напр., изменение показателя преломления n может быть вызвано нагревом среды лазерным излучением. Изменение темп-ры DT=aЕ2 (a — коэфф. поглощения света) приводит к изменению n от n0 до n=n0+(дn/дT)DT. Во мн. случаях существенным оказывается также эффект электрострикции (сжатие среды в световом поле Е). В сильном световом поле Е лазера электрострикц. давление, пропорц. Е2, изменяет плотность среды, что может привести к генерации звук. волн. С тепловыми эффектами связана самодефокусировка света.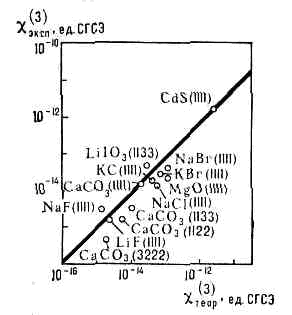 Рис. 1. Сравнение эксперим. значений кубичной восприимчивости c(3) для разл. кристаллов с теоретическими; т. к. c(3) — тензор 4-го ранга, то сравниваются конкретные компоненты тензора.Нелинейные восприимчивости c(2), c(3), c(4) и т. д.— новые параметры вещества (рис. 1). Изучение их дисперсии (зависимости от со) — предмет нелинейной спектроскопии. Для атомов методами квантовой механики удаётся рассчитать нелинейные восприимчивости любого порядка. Их дисперсия имеет сложный вид, так как резонансы возникают не только при совпадении частот действующих полей с собственными частотами атома, но и при совпадении с ними тех или иных комбинаций этих частот. В не слишком сильных лазерных полях совпадение результатов теории и эксперимента оказывается хорошим. Для простых молекул вблизи их колебательно-вращат. резонансов дисперсия нелинейной восприимчивости имеет много общего с дисперсией нелинейной восприимчивости атомов вблизи их электронных резонансов. Гораздо сложнее картина для электронных переходов в больших молекулах и конденсированных средах. Несмотря на то, что квантовомеханический расчёт в этих случаях невозможен, была развита феноменологическая теория, позволившая получить количественные результаты, во мн. случаях хорошо согласующиеся с экспериментом (рис. 1), и дать рецепты поиска новых нелинейно-оптич. материалов. В то время как значения c(2) для подавляющего большинства оптич. материалов отличаются между собой не более чем на один порядок, значения c(3) отличаются на три порядка. Это свидетельствует об особой физ. информативности нелинейных св-в в-ва.Оптические гармоники.На рис. 1 на вклейке к стр. 528 показано, как интенсивное монохроматич. излучение лазера на неодимовом стекле (l=1,06 мкм), проходя через оптически прозрачный кристалл ниобата бария, преобразуется в излучение с l=0,53 мкм, т. е. во 2-ю гармонику. При нек-рых условиях во 2-ю гармонику переходит более 60% энергии падающего излучения. Более сложные эффекты возникают, если в среде распространяются две или неск. интенсивных волн с разл. частотами, w1 и w2. Тогда наряду с гармониками каждой из волн (2w1, 2w2 и т. д.) возникают волны с комбинац. частотами (w1+ w2, w1-w2 и т. п.).
Рис. 1. Сравнение эксперим. значений кубичной восприимчивости c(3) для разл. кристаллов с теоретическими; т. к. c(3) — тензор 4-го ранга, то сравниваются конкретные компоненты тензора.Нелинейные восприимчивости c(2), c(3), c(4) и т. д.— новые параметры вещества (рис. 1). Изучение их дисперсии (зависимости от со) — предмет нелинейной спектроскопии. Для атомов методами квантовой механики удаётся рассчитать нелинейные восприимчивости любого порядка. Их дисперсия имеет сложный вид, так как резонансы возникают не только при совпадении частот действующих полей с собственными частотами атома, но и при совпадении с ними тех или иных комбинаций этих частот. В не слишком сильных лазерных полях совпадение результатов теории и эксперимента оказывается хорошим. Для простых молекул вблизи их колебательно-вращат. резонансов дисперсия нелинейной восприимчивости имеет много общего с дисперсией нелинейной восприимчивости атомов вблизи их электронных резонансов. Гораздо сложнее картина для электронных переходов в больших молекулах и конденсированных средах. Несмотря на то, что квантовомеханический расчёт в этих случаях невозможен, была развита феноменологическая теория, позволившая получить количественные результаты, во мн. случаях хорошо согласующиеся с экспериментом (рис. 1), и дать рецепты поиска новых нелинейно-оптич. материалов. В то время как значения c(2) для подавляющего большинства оптич. материалов отличаются между собой не более чем на один порядок, значения c(3) отличаются на три порядка. Это свидетельствует об особой физ. информативности нелинейных св-в в-ва.Оптические гармоники.На рис. 1 на вклейке к стр. 528 показано, как интенсивное монохроматич. излучение лазера на неодимовом стекле (l=1,06 мкм), проходя через оптически прозрачный кристалл ниобата бария, преобразуется в излучение с l=0,53 мкм, т. е. во 2-ю гармонику. При нек-рых условиях во 2-ю гармонику переходит более 60% энергии падающего излучения. Более сложные эффекты возникают, если в среде распространяются две или неск. интенсивных волн с разл. частотами, w1 и w2. Тогда наряду с гармониками каждой из волн (2w1, 2w2 и т. д.) возникают волны с комбинац. частотами (w1+ w2, w1-w2 и т. п.).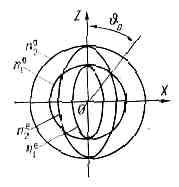 Рис. 2. Сечения поверхностей показателей преломления в кристалле КН2РО4 для частоты излучения неодимового лазера (индекс 1) и его 2-й гармоники (индекс 2). В плоскости OXZ сечения для обыкновенных волн (n0) — окружности, для необыкновенных волн (nе) — эллипсы. Под углом q0 к оптической оси OZ n01=ne2, а следовательно, равны и фазовые скорости осн. обыкновенной и 2-й гармоники необыкновенной волн.Генерация оптич. гармоник имеет много общего с умножением частоты в нелинейных элементах радиоустройств, однако в оптике эти эффекты явл. результатом вз-ствия со средой не колебаний, а волн. Т. к. свет распространяется в среде, размеры L к-рой существенно превышают l, суммарный эффект генерации гармоник на выходе зависит от фазовых соотношений между осн. волной и гармониками внутри среды; возникает своеобразная интерференция, способная либо усилить, либо ослабить эффект. Можно ожидать, что вз-ствие двух волн, напр. w и 2w, максимально, а следовательно, максимальна и перекачка энергии от осн. волны w к гармонике 2w, если их фазовые скорости равны (условие фазового синхронизма). С квант. точки зрения, это условие соответствует закону сохранения импульса k при слиянии или распаде фотонов. Для трёх волн условия синхронизма имеют вид: k3=k1+k2, где k1 k2 и k3 — импульсы фотонов (в ед. n).Равенство фазовых скоростей волн на разных частотах имеет место лишь в среде без дисперсии (см. ДИСПЕРСИЯ ВОЛН). Однако выяснилось, что отсутствие дисперсии можно имитировать, используя вз-ствие волн разной поляризации в анизотропной среде, в частности в кристаллах (рис. 2). В нек-рых кристаллах есть направления, вдоль к-рых фазовая скорость одинакова для основной обыкновенной волны и необыкновенной волны 2-й гармоники (см. КРИСТАЛЛООПТИКА и рис. 2). Этот метод резко повысил эффективность нелинейных волновых взаимодействий. Если в 1961 кпд оптических удвоителей частоты составлял 10-10—10-12, то современные удвоители имеют кпд -0,8.Оптич. умножители частоты используются для преобразования излучения ДВ лазеров в излучение KB диапазонов. Обычно для этой цели служат процессы генерации 2-й и 3-й гармоник, но в нек-рых случаях интерес представляют и нелинейные явления более высокого порядка. Благодаря нелинейной поляризации n-го порядка P(n)=c(n)ЕN световая волна частоты w возбуждает n-ю гармонику wn=nw, и при достаточно больших n использование умножения частоты позволяет сразу продвинуться достаточно далеко в KB область спектра.
Рис. 2. Сечения поверхностей показателей преломления в кристалле КН2РО4 для частоты излучения неодимового лазера (индекс 1) и его 2-й гармоники (индекс 2). В плоскости OXZ сечения для обыкновенных волн (n0) — окружности, для необыкновенных волн (nе) — эллипсы. Под углом q0 к оптической оси OZ n01=ne2, а следовательно, равны и фазовые скорости осн. обыкновенной и 2-й гармоники необыкновенной волн.Генерация оптич. гармоник имеет много общего с умножением частоты в нелинейных элементах радиоустройств, однако в оптике эти эффекты явл. результатом вз-ствия со средой не колебаний, а волн. Т. к. свет распространяется в среде, размеры L к-рой существенно превышают l, суммарный эффект генерации гармоник на выходе зависит от фазовых соотношений между осн. волной и гармониками внутри среды; возникает своеобразная интерференция, способная либо усилить, либо ослабить эффект. Можно ожидать, что вз-ствие двух волн, напр. w и 2w, максимально, а следовательно, максимальна и перекачка энергии от осн. волны w к гармонике 2w, если их фазовые скорости равны (условие фазового синхронизма). С квант. точки зрения, это условие соответствует закону сохранения импульса k при слиянии или распаде фотонов. Для трёх волн условия синхронизма имеют вид: k3=k1+k2, где k1 k2 и k3 — импульсы фотонов (в ед. n).Равенство фазовых скоростей волн на разных частотах имеет место лишь в среде без дисперсии (см. ДИСПЕРСИЯ ВОЛН). Однако выяснилось, что отсутствие дисперсии можно имитировать, используя вз-ствие волн разной поляризации в анизотропной среде, в частности в кристаллах (рис. 2). В нек-рых кристаллах есть направления, вдоль к-рых фазовая скорость одинакова для основной обыкновенной волны и необыкновенной волны 2-й гармоники (см. КРИСТАЛЛООПТИКА и рис. 2). Этот метод резко повысил эффективность нелинейных волновых взаимодействий. Если в 1961 кпд оптических удвоителей частоты составлял 10-10—10-12, то современные удвоители имеют кпд -0,8.Оптич. умножители частоты используются для преобразования излучения ДВ лазеров в излучение KB диапазонов. Обычно для этой цели служат процессы генерации 2-й и 3-й гармоник, но в нек-рых случаях интерес представляют и нелинейные явления более высокого порядка. Благодаря нелинейной поляризации n-го порядка P(n)=c(n)ЕN световая волна частоты w возбуждает n-ю гармонику wn=nw, и при достаточно больших n использование умножения частоты позволяет сразу продвинуться достаточно далеко в KB область спектра.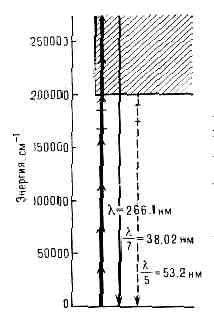 Рис. 3. Энергетич. схема генерации 5-й и 7-й оптич. гармоник в атомах Не; горизонтальными штрихами отмечены положения энергетич. уровней атома Не, заштрихована область сплошного спектра.Однако нелинейные восприимчивости c(n) быстро уменьшаются с ростом n(c(n)=1/E(n-1)a), и поэтому для получения заметного нелинейного эффекта необходимы достаточно мощные световые пучки. Предел здесь определяется не мощностью лазеров, а конкурирующими нелинейными явлениями в в-ве и прежде всего его оптич. пробоем. Поэтому возможности использования высших нелинейностей в той или иной среде обусловливаются в первую очередь её лучевой прочностью. Т. к. эта величина возрастает по мере сокращения длительности лазерного импульса, то используются сверхкороткие импульсы длительностью 10-11—10-12 с.В благородных газах или парах металлов предельные плотности мощности для пикосекундных лазерных импульсов значительно выше, чем в конденсиров. средах (1012—1013 Вт/см2). В этих условиях становится эффективной генерация 5-й и даже 7-й гармоник, обусловленная нелинейностями c(5) и c(7) (в газе отличны от нуля только нечетные члены в (2)). Указанные процессы были использованы для получения когерентного излучения в области далёкого вакуумного ультрафиолета. Мощные сверхкороткие лазерные импульсы с l=2661 нм возбуждали газообразный Не; на выходе кюветы с Не было зарегистрировано излучение 5-й (l=53,2 нм) и 7-й (l=38,02 нм) гармоник (рис. 3). Это пока кратчайшая длина волны когерентного излучения.Самофокусировка света. Самовоздействия.При мощности светового пучка, превышающей нек-рое критич. значение Ркр в среде, вместо обычной дифракц. расходимости первоначально параллельного пучка может наблюдаться его самосжатие. Величина Pкр различна для разных сред; для ряда органич. жидкостей Pкр=10—50 кВт; в нек-рых кристаллах и оптич. стёклах Ркр не превышает неск. Вт. Иногда, напр. при распространении излучения мощных импульсных лазеров в жидкостях, самосжатие носит характер «схлопывания» пучка, к-рое сопровождается настолько быстрым нарастанием интенсивности светового поля, что это может вызвать световой пробой, фазовые переходы и др. изменения состояния в-ва. В др. случаях, напр. при распространении излучения газовых лазеров непрерывного действия в стёклах, нарастание интенсивности поля также заметно, хотя и не является столь быстрым. Самосжатие в нек-ром смысле похоже на фокусировку пучка обычной линзой. Однако существенные различия наблюдаются за фокальной точкой; самосфокусированный пучок может образовывать квазистацнонарные нити (волноводное распространение), последовательность движущихся фокальных точек и т. п.
Рис. 3. Энергетич. схема генерации 5-й и 7-й оптич. гармоник в атомах Не; горизонтальными штрихами отмечены положения энергетич. уровней атома Не, заштрихована область сплошного спектра.Однако нелинейные восприимчивости c(n) быстро уменьшаются с ростом n(c(n)=1/E(n-1)a), и поэтому для получения заметного нелинейного эффекта необходимы достаточно мощные световые пучки. Предел здесь определяется не мощностью лазеров, а конкурирующими нелинейными явлениями в в-ве и прежде всего его оптич. пробоем. Поэтому возможности использования высших нелинейностей в той или иной среде обусловливаются в первую очередь её лучевой прочностью. Т. к. эта величина возрастает по мере сокращения длительности лазерного импульса, то используются сверхкороткие импульсы длительностью 10-11—10-12 с.В благородных газах или парах металлов предельные плотности мощности для пикосекундных лазерных импульсов значительно выше, чем в конденсиров. средах (1012—1013 Вт/см2). В этих условиях становится эффективной генерация 5-й и даже 7-й гармоник, обусловленная нелинейностями c(5) и c(7) (в газе отличны от нуля только нечетные члены в (2)). Указанные процессы были использованы для получения когерентного излучения в области далёкого вакуумного ультрафиолета. Мощные сверхкороткие лазерные импульсы с l=2661 нм возбуждали газообразный Не; на выходе кюветы с Не было зарегистрировано излучение 5-й (l=53,2 нм) и 7-й (l=38,02 нм) гармоник (рис. 3). Это пока кратчайшая длина волны когерентного излучения.Самофокусировка света. Самовоздействия.При мощности светового пучка, превышающей нек-рое критич. значение Ркр в среде, вместо обычной дифракц. расходимости первоначально параллельного пучка может наблюдаться его самосжатие. Величина Pкр различна для разных сред; для ряда органич. жидкостей Pкр=10—50 кВт; в нек-рых кристаллах и оптич. стёклах Ркр не превышает неск. Вт. Иногда, напр. при распространении излучения мощных импульсных лазеров в жидкостях, самосжатие носит характер «схлопывания» пучка, к-рое сопровождается настолько быстрым нарастанием интенсивности светового поля, что это может вызвать световой пробой, фазовые переходы и др. изменения состояния в-ва. В др. случаях, напр. при распространении излучения газовых лазеров непрерывного действия в стёклах, нарастание интенсивности поля также заметно, хотя и не является столь быстрым. Самосжатие в нек-ром смысле похоже на фокусировку пучка обычной линзой. Однако существенные различия наблюдаются за фокальной точкой; самосфокусированный пучок может образовывать квазистацнонарные нити (волноводное распространение), последовательность движущихся фокальных точек и т. п.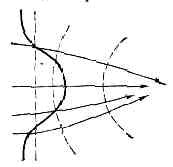 Рис. 4. Изменение хода лучей и самофокусировка света в среде с показателем преломления n, зависящим от интенсивности света; стрелками показан ход лучей; пунктир — поверхности постоянной фазы; сплошная линия — распределение интенсивности света.Явление самофокусировки обусловлено тем, что в сильном световом поле изменяется показатель преломления среды (в опыте, изображённом на рис. 2 на вклейке к стр. 528, это происходит за счёт нагрева стекла лазерным излучением). Если знак изменения n таков, что область, занятая пучком, становится оптически более плотной, то периферийные лучи отклоняются к центру пучка (на рис. 4 изображены фазовые фронты и ход лучей в ограниченном пучке, распространяющемся в среде, с показателем преломления; n=n0+n2Е2, где n0 — постоянная составляющая, не зависящая от Е, а n2>0. Поскольку фазовая скорость света v=c/n=c/(n0+n2E2), а поле Е на оси больше, чем на периферии, то фазовые фронты изгибаются и лучи отклоняются к оси пучка. Такая нелинейная рефракция может быть столь существенной (её величина нарастает вместе с концентрацией поля), что практически полностью подавляет дифракц. расходимость.
Рис. 4. Изменение хода лучей и самофокусировка света в среде с показателем преломления n, зависящим от интенсивности света; стрелками показан ход лучей; пунктир — поверхности постоянной фазы; сплошная линия — распределение интенсивности света.Явление самофокусировки обусловлено тем, что в сильном световом поле изменяется показатель преломления среды (в опыте, изображённом на рис. 2 на вклейке к стр. 528, это происходит за счёт нагрева стекла лазерным излучением). Если знак изменения n таков, что область, занятая пучком, становится оптически более плотной, то периферийные лучи отклоняются к центру пучка (на рис. 4 изображены фазовые фронты и ход лучей в ограниченном пучке, распространяющемся в среде, с показателем преломления; n=n0+n2Е2, где n0 — постоянная составляющая, не зависящая от Е, а n2>0. Поскольку фазовая скорость света v=c/n=c/(n0+n2E2), а поле Е на оси больше, чем на периферии, то фазовые фронты изгибаются и лучи отклоняются к оси пучка. Такая нелинейная рефракция может быть столь существенной (её величина нарастает вместе с концентрацией поля), что практически полностью подавляет дифракц. расходимость. В реальном лазерном импульсе мощность изменяется во времени и соответственно изменяется во времени фокальная длина нелинейной линзы. В результате возникает движущийся фокус. Скорость его движения может достигать 109 см/с. Учёт быстрого движения фокусов в сочетании с аберрациями нелинейной линзы во мн. случаях позволяет построить полную теорию явления самофокусировки.Обратный эффект — с а м о д е ф о к у с и р о в к а возникает, если среда в области, занятой световым пучком, становится оптически менее плотной (n2<0). В этом случае мощный лазерный пучок расходится гораздо быстрее, чем пучок малой интенсивности. Самодефокусировка наблюдается при распространении мощных лазерных пучков в атмосфере. Нелинейные волновые явления типа самофокусировки и самодефокусировки, в к-рых частота почти не изменяется, наз. самовоздействием света (эффекты типа генерации гармоник и смешения волн наз. нелинейными вз-ствиями). Наряду с самовоздействием волн, модулированных в пр-ве, наблюдается также самовоздействие волн, модулированных во времени. Распространение лазерного светового импульса в среде с показателем преломления вида: n= n1+n2E2 сопровождается искажением его формы и фазовой модуляцией.
В реальном лазерном импульсе мощность изменяется во времени и соответственно изменяется во времени фокальная длина нелинейной линзы. В результате возникает движущийся фокус. Скорость его движения может достигать 109 см/с. Учёт быстрого движения фокусов в сочетании с аберрациями нелинейной линзы во мн. случаях позволяет построить полную теорию явления самофокусировки.Обратный эффект — с а м о д е ф о к у с и р о в к а возникает, если среда в области, занятой световым пучком, становится оптически менее плотной (n2<0). В этом случае мощный лазерный пучок расходится гораздо быстрее, чем пучок малой интенсивности. Самодефокусировка наблюдается при распространении мощных лазерных пучков в атмосфере. Нелинейные волновые явления типа самофокусировки и самодефокусировки, в к-рых частота почти не изменяется, наз. самовоздействием света (эффекты типа генерации гармоник и смешения волн наз. нелинейными вз-ствиями). Наряду с самовоздействием волн, модулированных в пр-ве, наблюдается также самовоздействие волн, модулированных во времени. Распространение лазерного светового импульса в среде с показателем преломления вида: n= n1+n2E2 сопровождается искажением его формы и фазовой модуляцией. Рис. 5. Нитевидные разрушения оптич. стекла в поле мощного лазера; тонкая нить — след самофокусиров. светового пучка.В результате возникает сильное уширение спектра излучения и ширина спектра на выходе из среды в сотни и тысячи раз превышает ширину спектра на входе (самомодуляция). Эффекты самовоздействия определяют осн. черты поведения мощных световых пучков в большинстве сред, включая и активные среды самих лазеров. В частности, лавинное нарастание интенсивности светового поля при самофокусировке вызывает во мн. случаях оптич. пробой среды (рас. 5).Самопросветление и нелинейное поглощение.Среды, непрозрачные для слабого излучения, могут стать прозрачными для высокоинтенсивного излучения (просветление), и, наоборот, прозрачные материалы могут «затемняться» по отношению к мощному излучению (нелинейное поглощение). Это объясняется зависимостью коэфф. поглощения от интенсивности света. Если интенсивность резонансного (по отношению к поглощающей среде) излучения велика, существенная доля ч-ц среды переходит из основного в возбуждённое состояние и населённости её верх. и ниж. уровней выравниваются. Наступает т. н. насыщение резонансного перехода (стационарное или квазистационарное), в результате к-рого среда перестаёт поглощать, т. е. становится прозрачной для данного резонансного излучения. Именно этот механизм просветления среды изучался в работах Вавилова (см. выше).
Рис. 5. Нитевидные разрушения оптич. стекла в поле мощного лазера; тонкая нить — след самофокусиров. светового пучка.В результате возникает сильное уширение спектра излучения и ширина спектра на выходе из среды в сотни и тысячи раз превышает ширину спектра на входе (самомодуляция). Эффекты самовоздействия определяют осн. черты поведения мощных световых пучков в большинстве сред, включая и активные среды самих лазеров. В частности, лавинное нарастание интенсивности светового поля при самофокусировке вызывает во мн. случаях оптич. пробой среды (рас. 5).Самопросветление и нелинейное поглощение.Среды, непрозрачные для слабого излучения, могут стать прозрачными для высокоинтенсивного излучения (просветление), и, наоборот, прозрачные материалы могут «затемняться» по отношению к мощному излучению (нелинейное поглощение). Это объясняется зависимостью коэфф. поглощения от интенсивности света. Если интенсивность резонансного (по отношению к поглощающей среде) излучения велика, существенная доля ч-ц среды переходит из основного в возбуждённое состояние и населённости её верх. и ниж. уровней выравниваются. Наступает т. н. насыщение резонансного перехода (стационарное или квазистационарное), в результате к-рого среда перестаёт поглощать, т. е. становится прозрачной для данного резонансного излучения. Именно этот механизм просветления среды изучался в работах Вавилова (см. выше). Рис. 6. Схема пикосекундного спектрометра, предназначенного для резонансной спектроскопии первичных стадий процесса фотосинтеза. Сверхкороткие импульсы 2-й гармоники лазера на алюмоиттриевом гранате YAG с примесью Nd (l=0,53 мкм) возбуждают два перестраиваемых параметрич. генератора (ПГС) на кристаллах КДР и LiNbO3. Такие генераторы позволяют получить мощные сверхкороткие импульсы длительностью =1011 с на любой длине волны в диапазоне 0,66—2,7 мкм. При изучении кинетики фотосинтеза генератор на кристалле КДР использовался для селективного возбуждения фотореакц. центров, а другой— для зондирования наведённых изменений поглощения.Для получения эффекта насыщения в стационарных условиях необходима затрата нек-рой энергии, поэтому просветление среды сопряжено с определёнными потерями энергии светового пучка.В поле коротких световых импульсов, длительность к-рых меньше характерных времён релаксации среды (для газов =10-7—10-8с, для конденсиров. сред =10-11—10-12 с), наблюдается эффект просветления др. типа, наз. эффектом самоиндуцированной прозрачности. В этом случае короткий мощный световой импульс проходит через среду, вообще «не успев» поглотиться (слабое же квазинепрерывное излучение той же частоты может поглотиться этой средой практически полностью). Результатом вз-ствия такого очень короткого светового импульса со средой оказывается резкое уменьшение групповой скорости распространения светового импульса и изменение его формы. Эффекты нелинейного поглощения связаны с тем, что при вз-ствии интенсивного излучения частоты w0 с ч-цами заметную вероятность имеют многофотонные процессы.Н. о. и нелинейная спектроскопия.Практически все осн. нелинейные оптич. явления (генерация гармоник и смешение частот, самофокусировка, самодефокусировка и самомодуляция лазерных пучков, нелинейное поглощение и просветление, самоиндуцированная прозрачность и т. п.) легли в основу спектроскопич. методов, применяемых для исследования газов, жидкостей и тв. тел — методов нелинейной спектроскопии.Прикладная Н. о.Круг вопросов, связанных с использованием явлений Н. о. для создания новых источников когерентного оптич. излучения, преобразования частоты, детектирования, преобразования сигналов и изображений. Созданы мощные генераторы на длинах волн l=0,34 мкм (2-я гармоника рубинового лазера) и на 2-й гармонике лазера на стекле с примесью Nd. Пром-сть выпускает оптич. умножители частоты, предназначенные для преобразования частоты лазеров на неодимовом стекле или на алюмоиттриевом гранате с примесью Nd (l=1,06 мкм), позволяющие получить мощное когерентное излучение на волнах l=0,53 мкм (2-я гармоника), l=0,35 мкм (3-я гармоника) и l=0,26 мкм (4-я гармоника). Для этой цели подобраны кристаллы, обладающие высокой нелинейностью (большими значениями c) и удовлетворяющие условиям фазового синхронизма.Др. важный класс нелинейных оптич. устройств — перестраиваемые по частоте параметрические генераторы света. В основе их действия лежат нелинейные оптич. явления, связанные с нелинейностью, квадратичной по полю. В среде с поляризацией P=c(2)E2 наряду со «слиянием» фотонов (генерацией гармоник и суммарных частот) возможен обратный процесс — когерентный «распад» фотона частоты W на два фотона, частоты к-рых w1 и w2 удовлетворяют условию W=w1+w2. Процесс идёт эффективно, если одновременно выполнены условия волнового синхронизма: kW=k1+k2. На этом принципе основано действие параметрич. генератора света. При фиксированной частоте W (частоте накачки) частоты w1 и w2 можно варьировать в широких пределах (сохраняется лишь их сумма), изменяя параметры среды, влияющие на выполнение условий синхронизма. Параметрич. генератор света — удобный источник перестраиваемых по частоте сверхкоротких световых импульсов. На рис. 6 показана схема пикосекундного спектрометра с двумя параметрич. генераторами света (ПГС), применяемого в биологии. Нелинейные преобразователи частоты используются здесь для изучения процесса трансформации энергии оптич. возбуждения сложными мол. комплексами.Методы Н. о. открывают новые возможности для создания корреляц. спектрографов и спектрографов с пространств. разложением спектра (см. СПЕКТРАЛЬНЫЕ ПРИБОРЫ, ФУРЬЕ СПЕКТРОСКОПИЯ). На рис. 7 изображена схема нелинейного спектрографа с пространств. разложением спектра, в котором используется то обстоятельство, что д и с п е р с и я н а п р а в л е н и й с и н х р о н и з м а в нелинейных кристаллах может быть сильнее, нежели обычная дисперсия.
Рис. 6. Схема пикосекундного спектрометра, предназначенного для резонансной спектроскопии первичных стадий процесса фотосинтеза. Сверхкороткие импульсы 2-й гармоники лазера на алюмоиттриевом гранате YAG с примесью Nd (l=0,53 мкм) возбуждают два перестраиваемых параметрич. генератора (ПГС) на кристаллах КДР и LiNbO3. Такие генераторы позволяют получить мощные сверхкороткие импульсы длительностью =1011 с на любой длине волны в диапазоне 0,66—2,7 мкм. При изучении кинетики фотосинтеза генератор на кристалле КДР использовался для селективного возбуждения фотореакц. центров, а другой— для зондирования наведённых изменений поглощения.Для получения эффекта насыщения в стационарных условиях необходима затрата нек-рой энергии, поэтому просветление среды сопряжено с определёнными потерями энергии светового пучка.В поле коротких световых импульсов, длительность к-рых меньше характерных времён релаксации среды (для газов =10-7—10-8с, для конденсиров. сред =10-11—10-12 с), наблюдается эффект просветления др. типа, наз. эффектом самоиндуцированной прозрачности. В этом случае короткий мощный световой импульс проходит через среду, вообще «не успев» поглотиться (слабое же квазинепрерывное излучение той же частоты может поглотиться этой средой практически полностью). Результатом вз-ствия такого очень короткого светового импульса со средой оказывается резкое уменьшение групповой скорости распространения светового импульса и изменение его формы. Эффекты нелинейного поглощения связаны с тем, что при вз-ствии интенсивного излучения частоты w0 с ч-цами заметную вероятность имеют многофотонные процессы.Н. о. и нелинейная спектроскопия.Практически все осн. нелинейные оптич. явления (генерация гармоник и смешение частот, самофокусировка, самодефокусировка и самомодуляция лазерных пучков, нелинейное поглощение и просветление, самоиндуцированная прозрачность и т. п.) легли в основу спектроскопич. методов, применяемых для исследования газов, жидкостей и тв. тел — методов нелинейной спектроскопии.Прикладная Н. о.Круг вопросов, связанных с использованием явлений Н. о. для создания новых источников когерентного оптич. излучения, преобразования частоты, детектирования, преобразования сигналов и изображений. Созданы мощные генераторы на длинах волн l=0,34 мкм (2-я гармоника рубинового лазера) и на 2-й гармонике лазера на стекле с примесью Nd. Пром-сть выпускает оптич. умножители частоты, предназначенные для преобразования частоты лазеров на неодимовом стекле или на алюмоиттриевом гранате с примесью Nd (l=1,06 мкм), позволяющие получить мощное когерентное излучение на волнах l=0,53 мкм (2-я гармоника), l=0,35 мкм (3-я гармоника) и l=0,26 мкм (4-я гармоника). Для этой цели подобраны кристаллы, обладающие высокой нелинейностью (большими значениями c) и удовлетворяющие условиям фазового синхронизма.Др. важный класс нелинейных оптич. устройств — перестраиваемые по частоте параметрические генераторы света. В основе их действия лежат нелинейные оптич. явления, связанные с нелинейностью, квадратичной по полю. В среде с поляризацией P=c(2)E2 наряду со «слиянием» фотонов (генерацией гармоник и суммарных частот) возможен обратный процесс — когерентный «распад» фотона частоты W на два фотона, частоты к-рых w1 и w2 удовлетворяют условию W=w1+w2. Процесс идёт эффективно, если одновременно выполнены условия волнового синхронизма: kW=k1+k2. На этом принципе основано действие параметрич. генератора света. При фиксированной частоте W (частоте накачки) частоты w1 и w2 можно варьировать в широких пределах (сохраняется лишь их сумма), изменяя параметры среды, влияющие на выполнение условий синхронизма. Параметрич. генератор света — удобный источник перестраиваемых по частоте сверхкоротких световых импульсов. На рис. 6 показана схема пикосекундного спектрометра с двумя параметрич. генераторами света (ПГС), применяемого в биологии. Нелинейные преобразователи частоты используются здесь для изучения процесса трансформации энергии оптич. возбуждения сложными мол. комплексами.Методы Н. о. открывают новые возможности для создания корреляц. спектрографов и спектрографов с пространств. разложением спектра (см. СПЕКТРАЛЬНЫЕ ПРИБОРЫ, ФУРЬЕ СПЕКТРОСКОПИЯ). На рис. 7 изображена схема нелинейного спектрографа с пространств. разложением спектра, в котором используется то обстоятельство, что д и с п е р с и я н а п р а в л е н и й с и н х р о н и з м а в нелинейных кристаллах может быть сильнее, нежели обычная дисперсия.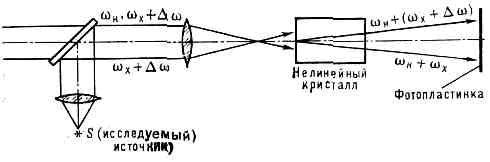 Рис. 7. Схема нелинейного спектрографа с пространств. разложением спектра. Частоты спектр. линий исследуемого источника wx+Dw складываются в нелинейном кристалле с частотой вспомогат. источника (генератора «накачки») wн. На выходе кристалла интенсивное излучение суммарной частоты wн+wх может наблюдаться только внутри весьма узкого угла, для к-рого выполняется условие волнового синхронизма.Спектральный анализ в этом случае сопровождается увеличением частоты света (что особенно важно при спектр. исследованиях в ИК области) и усилением исследуемого сигнала.Преобразование сигналов и изображений. Эффект сложения частот, лежащий в основе действия описанного спектрографа, находит также применение при регистрации слабых сигналов в ИК диапазоне. Если частота wх лежит в ИК диапазоне, а wн — в видимом, то в видимый диапазон попадает и суммарная частота wн+wх, причём коэфф. преобразования может быть ->1. В видимом же диапазоне регистрация сигнала производится с помощью высокочувствит. фотоэлектронного умножителя (ФЭУ). Т. о., система из нелинейного кристалла, в к-ром происходит сложение частот, и ФЭУ — чувствительный приёмник ИК излучения, применяемый, напр., в астрономии. Методы Н. о. стали использоваться в адаптивной оптике (см. ОБРАЩЁННЫЙ ВОЛНОВОЙ ФРОНТ).Заключение. С ростом напряжённости светового поля обнаруживаются всё новые нелинейные процессы. На первом этапе развития Н. о. использовался диапазон l от 1,06 до 0,3 мкм. Переход к ИК-лазерам привёл к открытию нелинейности, связанной с поведением носителей заряда в полупроводниках (в видимом диапазоне она практически не проявляется). При помощи мощных источников УФ излучения стали возможны исследования нелинейного поглощения в диэлектрич. кристаллах с широкой запрещённой зоной и жидкостях, умножение частоты в области вакуумного УФ и мягкого рентгеновского излучения. Уже наблюдались когерентные нелинейные эффекты в рентгеновской области.Успехи Н. о. стимулировали исследования нелинейных явлений в физике плазмы, акустике, радиофизике и вызвали интерес к общей теории нелинейных волн. В связи с Н. о. появились новые направления исследования в физике тв. тела и жидкостей, связанные с изучением их нелинейных св-в и оптич. прочности.
Рис. 7. Схема нелинейного спектрографа с пространств. разложением спектра. Частоты спектр. линий исследуемого источника wx+Dw складываются в нелинейном кристалле с частотой вспомогат. источника (генератора «накачки») wн. На выходе кристалла интенсивное излучение суммарной частоты wн+wх может наблюдаться только внутри весьма узкого угла, для к-рого выполняется условие волнового синхронизма.Спектральный анализ в этом случае сопровождается увеличением частоты света (что особенно важно при спектр. исследованиях в ИК области) и усилением исследуемого сигнала.Преобразование сигналов и изображений. Эффект сложения частот, лежащий в основе действия описанного спектрографа, находит также применение при регистрации слабых сигналов в ИК диапазоне. Если частота wх лежит в ИК диапазоне, а wн — в видимом, то в видимый диапазон попадает и суммарная частота wн+wх, причём коэфф. преобразования может быть ->1. В видимом же диапазоне регистрация сигнала производится с помощью высокочувствит. фотоэлектронного умножителя (ФЭУ). Т. о., система из нелинейного кристалла, в к-ром происходит сложение частот, и ФЭУ — чувствительный приёмник ИК излучения, применяемый, напр., в астрономии. Методы Н. о. стали использоваться в адаптивной оптике (см. ОБРАЩЁННЫЙ ВОЛНОВОЙ ФРОНТ).Заключение. С ростом напряжённости светового поля обнаруживаются всё новые нелинейные процессы. На первом этапе развития Н. о. использовался диапазон l от 1,06 до 0,3 мкм. Переход к ИК-лазерам привёл к открытию нелинейности, связанной с поведением носителей заряда в полупроводниках (в видимом диапазоне она практически не проявляется). При помощи мощных источников УФ излучения стали возможны исследования нелинейного поглощения в диэлектрич. кристаллах с широкой запрещённой зоной и жидкостях, умножение частоты в области вакуумного УФ и мягкого рентгеновского излучения. Уже наблюдались когерентные нелинейные эффекты в рентгеновской области.Успехи Н. о. стимулировали исследования нелинейных явлений в физике плазмы, акустике, радиофизике и вызвали интерес к общей теории нелинейных волн. В связи с Н. о. появились новые направления исследования в физике тв. тела и жидкостей, связанные с изучением их нелинейных св-в и оптич. прочности.
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- НЕЛИНЕЙНАЯ ОПТИКА
-
Содержание:
1. Сильные световые поля
2. Нелинейный отклик и нелинейные восприимчивости
3. Волновая нелинейная оптика. Управление продольными и поперечными взаимодействиями волн
4. Сильные нелинейности, нелинейные материалы
5. Нелинейная спектроскопия и нелинейная диагностика вещества
6. Параметрические процессы и параметрические преобразователи
7. Нелинейная динамика модулированных световых волн в кубичной среде
8. Рассеяние на оптически индуцированных когерентных элементарных возбуждениях - вынужденное рассеяние
9. Статистическая нелинейная оптика. Классические и квантовые сжатые состояния световых полей
10. Нелинейный отклик в физике воздействия лазерного излучения на вещество
11. Быстрое управление фазой и генерация фемтосекундных лазерных импульсов
12. Обработка информации и оптические компьютеры
Нелинейная оптика - раздел оптики, связанный с изучением и применением явлений, обусловленных нелинейным откликом вещества на световое поле.
Динамика электронов, атомов, молекул, конденси-ров. среды, возбуждаемых световым полем, принципиально нелинейна. Нелинейным оказывается даже движение свободного нерелятивистского электрона
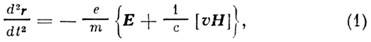
возбуждаемого гармонич. световой волной
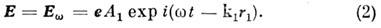
Действительно, поскольку u ~ Е, Е~ Н, второй член в правой части (1) пропорционален Е2.
Решая (1) методом возмущений (положив u/с <<1 и считая амплитуду напряжённости светового поля А1. умеренной), получим
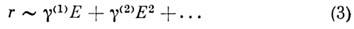
Из (3) непосредственно следует, что электрон, переизлучая поле на высших гармониках 2w, 3w, обнаруживает нелинейный отклик.
Нелинейный отклик связанного электрона, как правило, гораздо сильнее; он обусловлен, в первую очередь, нелинейным характером удерживающего его силового поля. Простейшая модель, проясняющая качественную сторону дела,- классич. ангармонич. осциллятор.
Для классич. "смещения" х связанного электрона имеем ур-ние
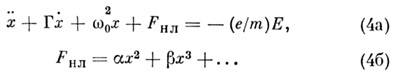
Считая нелинейный член F нл малым, выражения для наведённого дипольного момента атома или молекулы d = ex и макроскопич. поляризации Р (в изотропной среде Р = Nex; N - число частиц в единице объёма) можно получить, решая ур-ние (4) методом возмущений. Тогда ф-лы для d и Р имеют вид рядов по степеням поля Е. Коэф. разложения оказываются тензорами второго, третьего и более высоких порядков:
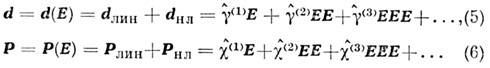
Пока в (4) можно пренебречь нелинейными членами (что характерно для хаотич. малоинтенсивного излучения большинства нелазерных источников света), для d и Р имеем:
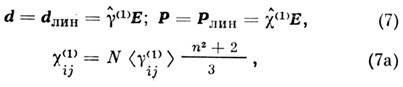
т. е. отклик среды линеен по полю и полностью описывается линейной поляризуемостью g(1) и линейной восприимчивостью c(1)- [Величина (n2 + 2)/3 - лоренцeв-ский фактор, или фактор действующего поля, характеризует действие соседних диполей.] Соотношения (7) являются квазистатич. материальными ур-ниями линейной оптики. Оптич. отклик в общем случае характеризуется набором поляризуемостей
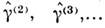 и нелинейных восприимчивостей
и нелинейных восприимчивостей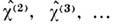
В лазерной оптике нелинейные слагаемые в (5) и (6) существенны, а обусловленные ими эффекты во мн. случаях доминируют. Более того, в "сверхсильных" световых полях мощных лазеров локальный нелинейный отклик сравнивается с линейным, Р лин~Р нл. (см. ниже).
Ясные представления о том, что законы линейной оптики, в частности суперпозиции принцип, носят приближённый характер и применимы лишь в области слабых полей, существовали и до появления лазеров. Первые прямые эксперименты по регистрации нели-нейностей в поглощении и преломлении света в флуоресцирующих кристаллах и стёклах были выполнены в 1920-30-х гг. С. И. Вавиловым с сотрудниками. Результатом нарушения принципа суперпозиции является известный ещё с прошлого века линейный эл.-оп-тич. эффект. Лежащее в его основе взаимодействие НЧ- и оптич. полей описывается квадратичным членом в разложении поляризации по полю:
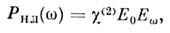
где Е0 - статич. (НЧ-) электрич. поле, изменяющее поляризацию (а следовательно, и показатель преломления) на оптич. частоте w.
Первым нелинейным эффектом, зарегистрированным с помощью лазера, стала генерация второй оптич. гармоники. В 1961 П. Франкен (P. Franken) с сотрудниками наблюдали удвоение частоты излучения рубинового лазера в кристалле кварца. Эффект описывается квадратичным по полю членом в нелинейной поляризации(6). Гармонич. поле (2) возбуждает в соответствии с (6) волну нелинейной поляризации на удвоенной частоте:
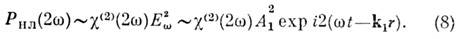
Эта волна - движущийся распределённый источник, переизлучающий световое поле гармоники E2w = = е2A2 ехр i(2wt-k2r).
В опытах Франкена генерация гармоник была очень слабым эффектом, кпд удвоения (относит. мощность гармоники)
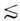 10-8. Однако уже к нач. 1963 кпд оптич. удвоителей достигали 20-30%. Решающую роль в этом сыграли реализация условий фазового синхронизма, согласование фазовых скоростей волн нелинейной поляризации и гармоники, осуществляющееся при 2k1 = k2 и приводящее к синфазному сложению полей гармоники, генерирующихся в разл. участках нелинейной среды. Т. о., даже в условиях, когда локальный нелинейный эффект мал (c(2)E << 1, Р нл << Р лин), накопление его на большой дистанции, управление "продольными" взаимодействиями приводят к сильному энергообмену между волнами.
10-8. Однако уже к нач. 1963 кпд оптич. удвоителей достигали 20-30%. Решающую роль в этом сыграли реализация условий фазового синхронизма, согласование фазовых скоростей волн нелинейной поляризации и гармоники, осуществляющееся при 2k1 = k2 и приводящее к синфазному сложению полей гармоники, генерирующихся в разл. участках нелинейной среды. Т. о., даже в условиях, когда локальный нелинейный эффект мал (c(2)E << 1, Р нл << Р лин), накопление его на большой дистанции, управление "продольными" взаимодействиями приводят к сильному энергообмену между волнами.Принципиальное значение для Н. о. имело создание лазеров с модулиров. добротностью (1962), позволяющих получать при длительности импульсов ~ 10-7- 10-8 с интенсивности ~1010-1011 Вт/см 2. Сильные поля лазеров с модулиров. добротностью позволили начать исследования нелинейных эффектов, кубичных по полю, определяемых c(3). С помощью этих лазеров получены 3-я и 4-я оптич. гармоники (1963-64), обнаружено явление вынужденного комбинац. рассеяния (1962). Оказалось, что в сильных лазерных полях взаимодействия электронных и колебат. движений в молекулах и кристаллах приводят к фазировке колебаний; рассеяние становится когерентным, интенсивность рассеянного света возрастает на много порядков.
В 1965 впервые наблюдалась самофокусировка света, зарегистрированы "поперечные" нелинейные взаимодействия: в нелинейной среде дифракционная расходимость мощного светового пучка подавляется нелинейной рефракцией, обусловленной нелинейной добавкой к показателю преломления (Dn = n2I, n2 ~ c(3)). В том же году запущен параметрический генератор света, в к-ром взаимодействие волн на квадратичной нелинейности используется для генерации когерентного излучения, плавно перестраиваемого по частоте в широком диапазоне.
Проблемы совр. Н. о. далеко выходят за рамки физ. и прикладной оптики в их традиц. понимании. Совр. Н. о. определяют след. направления: физика оптич. нелинейности и нелинейная спектроскопия; волновая Н. о.; воздействие сильного светового поля на вещество; прикладная Н. о.
Физика оптич. нелинейности и нелинейная спектроскопия. Совр. Н. о. сталкивается с разнообразными проявлениями нелинейного отклика разл. сред, сюда входят и прямые эксперименты по регистрации поляризации вакуума в сверхсильных световых полях. Спектроскопии, методы, основанные на изучении нелинейных свойств вещества, в частности дисперсии нелинейных восприимчивостей, оказались универсальными, позволили решать задачи, ранее недоступные оптич. технике.
Волновая нелинейная оптика. Нелинейность отклика приводит к взаимовлиянию, в т. ч. к сильному энергообмену волн с существенно разл. частотами и волновыми векторами, к нелинейным изменениям частотного и угл. спектров квазимонохроматич. квазиплоских волн (самовоздействиям). В процессе волновых взаимодействий и самовоздействий нелинейно изменяется и состояние поляризации волн - возникают поляризац. нелинейные эффекты.
Многообразные волновые взаимодействия и самовоздействия фактически определяют гл. черты поведения мощных лазерных пучков в материальной среде. Разработка эфф. методов управления продольными и поперечными нелинейными взаимодействиями позволила реализовать в оптике разнообразные эффекты нелинейной волновой динамики - параметрич. взаимодействия, ударные волны, генерацию структур, солитоны, спиральные волны, турбулентность.
Физика воздействия сильного cветового поля на вещество. Нелинейный отклик среды, нелинейные оптич. явления играют важную, а зачастую и решающую роль в механизмах лазерного возбуждения и релаксации сильнонеравно-весных состояний в атомах, молекулах и конденсиров. средах. На использовании оптич. нелинейности базируются и уникальные по быстродействию (временное разрешение ~ 10-15 с) и спектральному разрешению методы лазерной диагностики неравновесных состояний, быстрых превращений в веществе.
Прикладная нелинейная оптика. Преобразование частотного и угл. спектров, быстрое управление амплитудой и фазой световых волн, являющиеся следствием нелинейных взаимодействий и самовоздействий, лежат в основе действия широкого класса нелинейнооптич. устройств. Кроме традиц. преобразователей частоты и параметрич. генераторов, в прикладной Н. о. разработаны системы нелинейной адаптивной оптики, эфф. компрессоры сверхкоротких световых импульсов, бистабильные и мультистабильные элементы быстродействующих цифровых и аналоговых оптич. процессоров.
Т. о., мн. проблемы Н. о. тесно переплетаются с задачами атомной и молекулярной физики, физики твёрдого тела, электроники и технологии. При всём многообразии направлений исследований важнейшими продолжают оставаться: физика и техника генерации сильных световых полей; физика оптич. нелинейности и разработка нелинейных материалов; разработка методов управления продольными и поперечными взаимодействиями световых волн в нелинейных средах.
Величина нелинейного эффекта определяется напряжённостью светового поля, значением нелинейной восприимчивости и эфф. пространственным масштабом нелинейного взаимодействия.
1. Сильные световые поля
Естественный для Н. о. масштаб напряжённости поля - напряжённость внутриатомного поля Е а. Можно ожидать, что при Е = Е а нелинейный отклик сравнивается по величине с линейным:
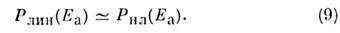
Максимальная в ряду внутриатомных полей напряжённость поля в атоме водорода
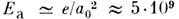 В/см достигается в световом пучке с интенсивностью
В/см достигается в световом пучке с интенсивностью 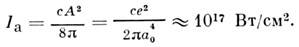
Для получения таких интенсивностей необходимо располагать лазерными системами, генерирующими излучение мощностью W
 1 ТВт (1012 Вт). Фокусировка излучения в пятно площадью а
1 ТВт (1012 Вт). Фокусировка излучения в пятно площадью а  10-6 см 2, вполне реальная в видимом и ближнем ИК-диапазоне, приводит в этом случае к I = W/s
10-6 см 2, вполне реальная в видимом и ближнем ИК-диапазоне, приводит в этом случае к I = W/s .1018 Вт/см 2.
.1018 Вт/см 2.С помощью лазеров с модулиров. добротностью (t и
 10-8-10-9 с) сверхсильные поля можно получить только в уникальных мультикилоджоульных установках, предназначенных для экспериментов по УТС. Поэтому огромное значение для Н. о. имели освоение техники генерации пико- и фемтосекундных импульсов, разработка методов сжатия лазерных импульсов, "фокусировка во времени" (рис. 1).
10-8-10-9 с) сверхсильные поля можно получить только в уникальных мультикилоджоульных установках, предназначенных для экспериментов по УТС. Поэтому огромное значение для Н. о. имели освоение техники генерации пико- и фемтосекундных импульсов, разработка методов сжатия лазерных импульсов, "фокусировка во времени" (рис. 1).При t и
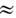 10-13-10-14 с переход к сверхсильным полям возможен при энергиях импульса 0,1 Дж.
10-13-10-14 с переход к сверхсильным полям возможен при энергиях импульса 0,1 Дж.Рис. 1. Диаграмма энергия -длительность лазерного импульса t и; линиями указаны уровни равной мощ ности. Свехсильным полям соответствует мощность > 1 ТВт.
Именно такими методами получены (1989) интенсивности I
 1019 Вт/см 2, при к-рых напряжённость светового поля почти на порядок превосходит атомное поле. При Е> Е а происходит радикальное изменение структуры вещества; дискретная структура атомных уровней практически исчезает, оптич. отклик определяется переходами в непрерывном спектре. Это означает, что при Е >= Е а на смену Н. о. атомов и молекул приходит нелинейная электронная физика. В действительности "динамич. диапазон" Н. о. атомов и молекул существенно уже. Конденсиров. среда, не слишком разреженный газ ионизуются при интенсивностях I = I пр << Ia(I пр - порог пробоя). Эффект связан с лавинным размножением свободных электронов, набирающих энергию в процессе столкновений в поле световой волны. При достижении критич. концентрации электронов N кp~ ~1016 см -3 возникает лавинный световой пробой (см. Оптические разряды). Возможность достичь N кр определяется плотностью световой энергии; поэтому I пр ~ ~1/t и, т. е. порог светового пробоя возрастает с уменьшением длительности лазерного импульса.
1019 Вт/см 2, при к-рых напряжённость светового поля почти на порядок превосходит атомное поле. При Е> Е а происходит радикальное изменение структуры вещества; дискретная структура атомных уровней практически исчезает, оптич. отклик определяется переходами в непрерывном спектре. Это означает, что при Е >= Е а на смену Н. о. атомов и молекул приходит нелинейная электронная физика. В действительности "динамич. диапазон" Н. о. атомов и молекул существенно уже. Конденсиров. среда, не слишком разреженный газ ионизуются при интенсивностях I = I пр << Ia(I пр - порог пробоя). Эффект связан с лавинным размножением свободных электронов, набирающих энергию в процессе столкновений в поле световой волны. При достижении критич. концентрации электронов N кp~ ~1016 см -3 возникает лавинный световой пробой (см. Оптические разряды). Возможность достичь N кр определяется плотностью световой энергии; поэтому I пр ~ ~1/t и, т. е. порог светового пробоя возрастает с уменьшением длительности лазерного импульса.Конкретные значения I пр, вид зависимости I пр(t и) определяются прежде всего соотношением частоты света со и резонансной частоты вещества w а.
Представления о порядках величин можно дать для существенно нерезонансного случая w/w а << 1. В этой ситуации пробой прозрачных кристаллов и стёкол в поле импульсов длительностью t и
 10-8 с происходит при I пр
10-8 с происходит при I пр 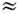 1010-1011 Вт/см 2. При t и
1010-1011 Вт/см 2. При t и  10-14 с верх. граница интенсивностей, при к-рых конденсиров. среда ещё не успевает ионизоваться, повышается до значений I пр
10-14 с верх. граница интенсивностей, при к-рых конденсиров. среда ещё не успевает ионизоваться, повышается до значений I пр 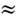 1013 -1014 Вт/см 2. При I= I т
1013 -1014 Вт/см 2. При I= I т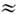 1015 Вт/см 2 атом ионизуется за счёт туннелирования электрона в световом поле за время порядка светового периода; этим определяется предельная оптич. прочность вещества в нерезонансных условиях. При I >= I т << I а [в нерезонансном случае
1015 Вт/см 2 атом ионизуется за счёт туннелирования электрона в световом поле за время порядка светового периода; этим определяется предельная оптич. прочность вещества в нерезонансных условиях. При I >= I т << I а [в нерезонансном случае 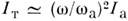 ] линейный и нелинейный отклики вещества определяются фактически откликом квазисвободных электронов.
] линейный и нелинейный отклики вещества определяются фактически откликом квазисвободных электронов.В световом поле напряжённостью
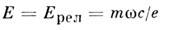
энергия осцилляции электрона становится сравнимой с энергией покоя. Соответственно, т. н. релятивистская интенсивность
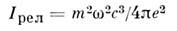
характеризует границу релятивистской Н. о. свободных электронов [при Е= Е релu
 с в (1) и вклад, обусловленный силой Лоренца, уже нельзя рассматривать как малое возмущение].
с в (1) и вклад, обусловленный силой Лоренца, уже нельзя рассматривать как малое возмущение].Для частот, соответствующих видимому диапазону, I рел
 1019 Вт/см 2 - величина, уже достигнутая в эксперименте.
1019 Вт/см 2 - величина, уже достигнутая в эксперименте.Получение сверхсильных полей позволяет экспериментально наблюдать эффекты нелинейной квантовой электродинамики. В полях напряжённостью Е
 1016 В/см (I
1016 В/см (I  1030 Вт/см 2) возможна генерация электронно-позитронных пар в вакууме ("оптич. пробой вакуума"). Хотядостижение таких полей пока представляется проблематичным, взаимодействие уже реализованных мощных лазерных импульсов с релятивистскими электронами может привести к наблюдению ряда принципиальных эффектов. При I > > 1020 Вт/см 2 реализуются условия наблюдения нелинейного томсоновского и нелинейного комптоновского рассеяний; возможна регистрация влияния лазерного поля на b-распад. При I > 1023 - 1024 Вт/см 2 возможно наблюдение черепковского излучения в вакууме, поляризованном мощной световой волной.
1030 Вт/см 2) возможна генерация электронно-позитронных пар в вакууме ("оптич. пробой вакуума"). Хотядостижение таких полей пока представляется проблематичным, взаимодействие уже реализованных мощных лазерных импульсов с релятивистскими электронами может привести к наблюдению ряда принципиальных эффектов. При I > > 1020 Вт/см 2 реализуются условия наблюдения нелинейного томсоновского и нелинейного комптоновского рассеяний; возможна регистрация влияния лазерного поля на b-распад. При I > 1023 - 1024 Вт/см 2 возможно наблюдение черепковского излучения в вакууме, поляризованном мощной световой волной.2. Нелинейный отклик и нелинейные восприимчивости
Нелинейный отклик свободных и связанных "оптич." электронов - универсальная, но не единственная причина возникновения нелинейных оптич. явлений. Существенными оказываются нелинейные колебания многоатомных молекул и кристаллич. решётки, возбуждение светом явлений дрейфа, диффузии зарядов в кристаллах (фоторефрактивный эффект), индуцированная световой волной ориентация анизотропных молекул в жидкостях и жидких кристаллах (оптический Керра эффект), электрострикция, разл. тепловые эффекты и т. п. Перечисленные механизмы приводят к появлению оптич. нелинейностей, существенно различающихся по величине и времени установления нелинейного отклика t нл. Для наиб. быстрой нерезонансной электронной нелинейности t нл =<10-14 с, для инерционной тепловой нелинейности t нл > 10-3 с.
Слабый локальный нелинейный отклик. В большинстве практически интересных случаев локальный нелинейный отклик много меньше линейного ( Р нл<< Р лин) и нелинейные свойства среды хорошо описываются раз-ложениями (5), (6), набором гиперполяризуемостей
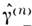 и нелинейных восприймчивостей
и нелинейных восприймчивостей 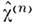 .
.В световом поле
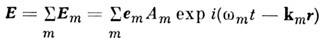
возникает бесконечный набор волн нелинейной поляризации на частотах
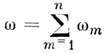
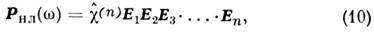
где определяющая макроскопич. нелинейный отклик спектральная компонента тензора ( п + 1)-го ранга
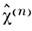 :
: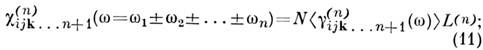
здесь
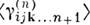 - усреднённый по ориентациям атомов или молекул тензор гиперполяризуемости, L(n)- фактор локального поля -поправка, учитывающая ди-поль-дипольное взаимодействие (обобщение лоренцевского фактора)
- усреднённый по ориентациям атомов или молекул тензор гиперполяризуемости, L(n)- фактор локального поля -поправка, учитывающая ди-поль-дипольное взаимодействие (обобщение лоренцевского фактора)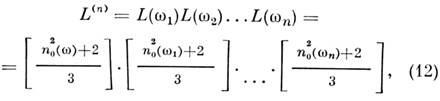
n0 (wm) - линейный показатель преломления. Ф-ла (11) является естеств. обобщением соотношения (7а). Расчёт величин g (п) и c(n) должен основываться на микроскопических теоретич. моделях. Информацию о нелинейном отклике даёт и феноменoлогич. теория, апеллирующая к общим свойствам симметрии среды, рассматривающая такие простые модельные системы, как классич. ангар-монич. осциллятор, квантовая двухуровневая система.
Квадратичные нелинейные восприимчивости. Младший нелинейный член в разложении (6) - квадратичный по полю
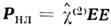 . Квадратичная нелинейная восприимчивость
. Квадратичная нелинейная восприимчивость 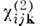 - тензор 3-го ранга; поэтому оптич. эффекты, квадратичные по полю, возникают только в средах, не имеющих центра симметрии. В квадратичной среде бигармонич. световое поле
- тензор 3-го ранга; поэтому оптич. эффекты, квадратичные по полю, возникают только в средах, не имеющих центра симметрии. В квадратичной среде бигармонич. световое поле 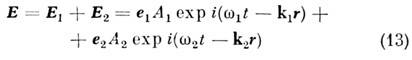
возбуждает волны нелинейной поляризации на частотах 2w1, 2w2, w1 bw2, являющихся результатом трёх-частотных (трёхфотонных) взаимодействий вида w = wi b wj (i,j = 1,2). Соответствующие спектральные компоненты тензора восприимчивости c(3)(2wi), c(2)(w1 b w2) связаны с быстрыми (электронными) механизмами нелинейного отклика, для к-рых t нл<= <= wi-1
 10-14 с. Эти процессы приводят к модуляции показателя преломления с оптич. частотой. Наиб. важный среди них - нерезонансный нелинейный отклик связанных оптич. электронов. Пользуясь (9), можно оценить c(2):
10-14 с. Эти процессы приводят к модуляции показателя преломления с оптич. частотой. Наиб. важный среди них - нерезонансный нелинейный отклик связанных оптич. электронов. Пользуясь (9), можно оценить c(2):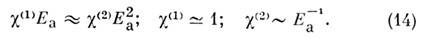
Если взять для Е а значение для атома водорода, то c(2) ~ 10-7 [СГС]. Реальные значения c(2) (2w) (в видимом диапазоне) для диэлектриков лежат в пределах от 10-9 [СГС] (кварц) до 1,7.10-8 СГС для одного из наиб. нелинейных кристаллов Ba2NaNb5O15. Существенно больше значения c(2) (2w) в полупроводниках; в GaAs на l1 = 1,06 мкм c(2)(2w)
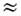 5,2.10-7 СГС; в кристалле Те в ИК-диапазоне (l = 10,6 мкм) c(2)
5,2.10-7 СГС; в кристалле Те в ИК-диапазоне (l = 10,6 мкм) c(2) 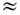 2,2.10-6 СГС. Т. о., в средах, линейные восприимчивости к-рых различаются меньше чем на порядок, различие в величинах нелинейного отклика достигает почти четырёх порядков. Для нелинейностей более высокого порядка по полю сказанное проявляется ещё сильнее (см. ниже). Количеств. расчёт c(2) кристаллов основывается в большинстве случаев на полуфеноменологич. моделях. Структуру квадратичного нелинейного отклика можно определить с помощью модели классич. ан-гармонич. осциллятора. Полагая в (4 б) F нл.= a х2 и подставляя в (4а) поле (13), методом возмущений получим d= g(1) E+ g(2) Е2 и
2,2.10-6 СГС. Т. о., в средах, линейные восприимчивости к-рых различаются меньше чем на порядок, различие в величинах нелинейного отклика достигает почти четырёх порядков. Для нелинейностей более высокого порядка по полю сказанное проявляется ещё сильнее (см. ниже). Количеств. расчёт c(2) кристаллов основывается в большинстве случаев на полуфеноменологич. моделях. Структуру квадратичного нелинейного отклика можно определить с помощью модели классич. ан-гармонич. осциллятора. Полагая в (4 б) F нл.= a х2 и подставляя в (4а) поле (13), методом возмущений получим d= g(1) E+ g(2) Е2 и 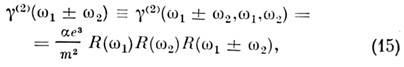
где
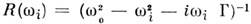 - резонансные множители, Г - полуширина линии поглощения. Тогда для c(2) [ср. (11)] получим:
- резонансные множители, Г - полуширина линии поглощения. Тогда для c(2) [ср. (11)] получим: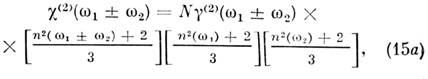
поскольку в кристалле элементарные "ячейки" ориентированы одинаково. К аналогичным ф-лам для g(2) и c(2) приводит и модель двухуровневой системы, в к-рой вместо классич. фактора D =a е3/т2. появляется произведение трёх матричных элементов переходов
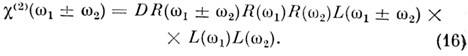
Кубичная нелинейная восприимчивость ci(3)kl, яв-ляясь тензором 4-го ранга, отлична от нуля в центро-симметричных средах: в газах, жидкостях, аморфных и кристаллич. твёрдых телах. В этих средах в результате четырёхчастотных (четырёхфотонных) взаимодействий вида w = wi b wj b wk (i,j,k= 1, 2, 3) бигармонич. поле (13) возбуждает широкий спектр волн нелинейной поляризации на комбинац. частотах и гармониках 3w1, 3w2, 2w1 b w2, 2w2 b w1 и т. п. Кубичные восприимчивости
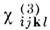 (3wi, wi, wi, wi),
(3wi, wi, wi, wi), 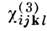 (2w1 b bw2, w1, w1 bw2) и т. н. для сильно различающихся частот w1 и w2 обусловлены малоинерционными (напр., электронными) механизмами нелинейного отклика. Для грубой оценки спектральной компоненты c(3)(3w), связанной с нерезонансным электронным откликом конденсиров. среды, можно полагать [ср. с (14)] c(3)(3w) ~ Е-2. Оценка c(3)(3w)
(2w1 b bw2, w1, w1 bw2) и т. н. для сильно различающихся частот w1 и w2 обусловлены малоинерционными (напр., электронными) механизмами нелинейного отклика. Для грубой оценки спектральной компоненты c(3)(3w), связанной с нерезонансным электронным откликом конденсиров. среды, можно полагать [ср. с (14)] c(3)(3w) ~ Е-2. Оценка c(3)(3w)  10-13-10-14 СГС близка к значениям, измеряемым в оптически прозрачных жидкостях и диэлектриках.
10-13-10-14 СГС близка к значениям, измеряемым в оптически прозрачных жидкостях и диэлектриках.Поскольку c(3) отлична от нуля в газах, в её поведении гораздо сильнее, чем в c(2), проявляются индивидуальные свойства атомов и молекул. Особенно ярко они выражены в резонансных свойствах c(3) (для разреженного газа c(3) = Ng(3)). На рис. 2 приведены теоре-тич. график дисперсии g(3) и диаграмма энергетич. уровней для атомов Na. Отчётливо видны сильные возрастания кубич. восприимчивости вблизи резонансов.
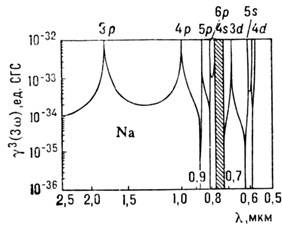
Рис. 2. Теоретические значения кубичной гиперполяризуемости g(3)(3w) атома Na, ответственной за генерацию третьей гармоники в зависимости от длины волны основного излучения l.
Четырёхчастотные нелинейные взаимодействия па кубичной нелинейности приводят не только к генерации волн на новых частотах, но и к возникновению волн нелинейной поляризации на частотах исходных волн:
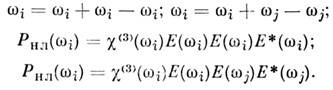
В результате такого самовоздействия, или кроссмоду-ляции, возникает нелинейная добавка n2 к показателю преломления для волны частоты wi.
Полный показатель преломления кубичной среды
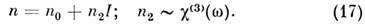
Если выразить n2 в [см 2/кВт], то
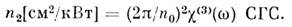
Обусловленная быстрым нерезонансным откликом оп-тич. электронов нелинейная добавка n2 относительно невелика. Полагая c(3)(w)
 10-14 СГС, имеем n2
10-14 СГС, имеем n2  10-13 см 2/кВт; таковы прибл. значения n2 для мн. кристаллов и жидкостей. В таком случае даже для интенсивностей, близких к пробойным, I
10-13 см 2/кВт; таковы прибл. значения n2 для мн. кристаллов и жидкостей. В таком случае даже для интенсивностей, близких к пробойным, I  I пр,
I пр,Dn =n2I пр<< n0.
Имеется много других, хотя и более инерционных, механизмов, приводящих к существенно более сильной нелинейности показателя преломления. К ним относятся резонансные нелинейности в полупроводниках (экситонные резонансы в двумерных структурах), фо-торефрактивный эффект в неорганич. кристаллах, ориентация анизотропных молекул в световом поле и оптич. нагрев среды. Диапазон значений нелинейного параметра n2 превышает десять порядков (рис. 3). Несмотря на существ. различие физ. механизмов нелинейности, многочисл. данные неплохо укладываются на прямые п2 ~t нл; возрастание величины n2 сопровождается увеличением инерционности отклика.
К ориентац. механизмам в жидких кристаллах, приводящим к n2 > 0,1 см 2/кВт, с полным основанием применим термин "гигантские оптич. нелинейности".
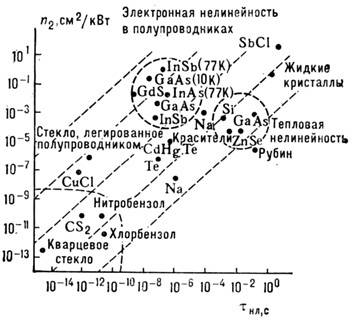
Рис. 3. Значения нелинейного коэффициента n2 для оптических материалов на плоскости n2, t нл.
Высшие нелинейности. Квадратичная и кубичная нелинейности доминируют в подавляющем большинстве практически важных случаев. Нелинейности более высокого порядка быстро убывают с номером п,c(n) ~ Еa-(n-1) (под Е а. следует понимать нек-рое эфф. "атомное" поле, различное для разных механизмов нелинейности).
В кристаллах в поле интенсивных сверхкоротких импульсов зарегистрированы эффекты, обусловленные быстрыми (электронными) нелинейностями P нл(4) ~ c(4)E4 и
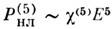 . В атомарных газах при ин-тенсивностях I ~ 1011 Вт/см 2 измерены нелинейные эффекты, обусловленные
. В атомарных газах при ин-тенсивностях I ~ 1011 Вт/см 2 измерены нелинейные эффекты, обусловленные 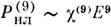 .
.Нелинейный отклик в сверхсильных полях. В сверхсильных световых полях ( Е
 Е а )описание нелинейного отклика, базирующееся на методе возмущений, разложении нелинейной поляризации в ряд по степеням поля, теряет силу; в значит. мере утрачивает смысл и понятие нелинейной восприимчивости. В экспериментах по генерации оптич. гармоник в атомах инертных газов при интенсивностях I ~ 1014-1015 Вт/см 2 были зарегистрированы нечётные гармоники вплоть до 21-й. Теоретическая интерпретация эффекта базируется на численном анализе нелинейного отклика одноэлектронного атома, никак не связанном с методом возмущений.
Е а )описание нелинейного отклика, базирующееся на методе возмущений, разложении нелинейной поляризации в ряд по степеням поля, теряет силу; в значит. мере утрачивает смысл и понятие нелинейной восприимчивости. В экспериментах по генерации оптич. гармоник в атомах инертных газов при интенсивностях I ~ 1014-1015 Вт/см 2 были зарегистрированы нечётные гармоники вплоть до 21-й. Теоретическая интерпретация эффекта базируется на численном анализе нелинейного отклика одноэлектронного атома, никак не связанном с методом возмущений.3. Волновая нелинейная оптика. Управление продольными и поперечными взаимодействиями волн
Распространение световых волн в слабонелинейной среде описывается неоднородным волновым ур-нием
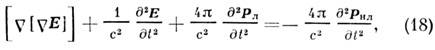
где внеш. силой является волна нелинейной поляризации Р нл(r, t). Последняя возбуждает вынужденную эл.-магн. волну, имеющую те же частоту и волновой вектор, что и волна нелинейной поляризации. Интерференция вынужденных волн со свободными волнами среды определяет динамику развития нелинейного волнового процесса во времени и в пространстве. Поскольку характер интерференции свободных и вынужденных волн существенно зависит от дисперсии среды, дисперсионные параметры решающим образом влияют на формирование нелинейных волн. В электродинамике сильнодиспергирующих слабонелинейных сред принято выделять нелинейные взаимодействия волн с разл. частотами и волновыми векторами и самовоздействия волн, обусловленные зависимостью комплексного показателя преломления от интенсивности.
Строгое разграничение нелинейных волновых процессов на взаимодействия и самовоздействия справедливо лишь для плоских монохроматич. волн, для к-рых самовоздействия проявляются как самоиндуциров. изменения поглощения и фазовой скорости волны. Для реальных модулированных во времени и пространстве световых волн эта классификация условна. Самовоздействия волновых пакетов и пучков в кубичной среде (самоиндуциров. изменения формы модуляции) обусловлены четырёхфотонными взаимодействиями разл. компонент частотного и угл. спектров, продольными и поперечными взаимодействиями. Однако термины "взаимодействия" и "самовоздействия" широко используются и для модулиров. волн. В совр. Н. о. говорят о взаимодействиях, имея в виду взаимодействия волн с сильно различающимися частотами - процессы типа генерации гармоник, суммарных и разностных частот, пара-метрич. усиления и параметрич. генерации. Нелинейные преобразования частотного и угл. спектров квази-монохроматич. квазиплоских волн в средах с нечётными по полю нелинейностями относят к самовоздействиям.
Дело не только в терминологии, существенно различаются теоретич. подходы, физ. образы, используемые при исследовании взаимодействий и самовоздействий. В описании взаимодействий первоочередной интерес представляет динамика распределения энергии по спектру, а в описании самовоздействий главное - поиски автомодельных решений, стационарных волн, неустой-чивостей и т. п.
Приближённые уравнения нелинейной геометрической оптики; связанные волны. Для большинства практически интересных задач Н. о. ур-ние (18) можно упростить, пользуясь методом медленно меняющихся амплитуд. Для плоских волн, распространяющихся в слабонелинейной среде,
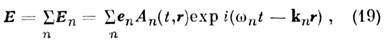
в первом приближении теории дисперсии полагая, что комплексные амплитуды А п медленно изменяются на длине волны ln и периоде Т п =2p/wn, вместо (6), (18) получаем систему п связанных ур-ний 1-го порядка
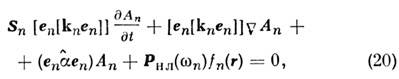
где Р нл(wn) - спектральные компоненты нелинейной поляризации на частоте wn;
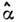 - тензор, описывающий потери в среде; Sn - лучевой вектор; fn (r) - фактор, описывающий интерференцию свободных и вынужденных волн.
- тензор, описывающий потери в среде; Sn - лучевой вектор; fn (r) - фактор, описывающий интерференцию свободных и вынужденных волн.Дифракция, дисперсионное расплывание волновых пакетов. Наиб. адекватна нелинейным задачам гонгов-ская трактовка дифракции (см. Дифракция воли). Её матем. аппарат никак не связан с принципом суперпозиции и базируется на параболич. ур-нии для комплексной амплитуды (см. Волны), описывающем "поперечную" диффузию поля, что тесно связано с методом медленно меняющихся амплитуд.
Системой связанных параболич. ур-ний
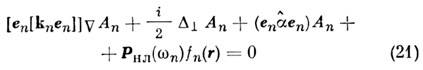
описывается распространение монохроматич. волновых пучков в нелинейной среде. Аналогичные по структуре ур-ния описывают и взаимодействия плоских волновых пакетов в нелинейной диспергирующей среде. Во втором приближении теории дисперсии, рассматривая для простоты плоский пакет в изотропной среде, получим нараболич. ур-ние вида
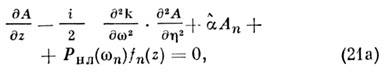
где h = t - z/u, u - групповая скорость пакета.
Локальные и накапливающиеся нелинейные эффекты. В протяжённой среде, характерный размер к-рой существенно превышает длину волны, эффективность нелинейного взаимодействия определяется величиной локального нелинейного отклика (величиной ~ c(2)E в квадратичной среде и c(3) Е2 ~ в кубичной) и условиями интерференции свободных и вынужденных волн.
Сильные нелинейные взаимодействия (сильный энергообмен между взаимодействующими волнами) удаётся получить и в слабонелинейной среде, в к-рой c(2) Е<< 1, c(3) Е2<< 1. Малость локального нелинейного отклика компенсируется организацией накапливающихся взаимодействий. Последнего можно добиться за счёт подбора дисперсионных свойств среды. Пример этого - генерация 2-й оптич. гармоники в двулучепреломляю-щем кристалле. В приближении геом. оптики система связанных ур-ний (20) сводится к двум ур-ниям 1-го порядка для амплитуд осн. волны А1 и 2-й гармоники А2 (без учёта потерь):
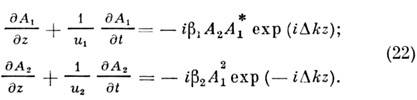
Здесь u1, u2 - групповые скорости, b1 =
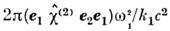 , b2 =
, b2 =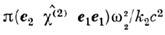 -
- коэф. нелинейной связи, ось z направлена вдоль k1, Ai = ri ехр(iji). Расстройка волновых векторов Dk= k2 -2k1 определяет картину интерференции свободной (волновое число k2) и вынужденной (волновое число 2k1 )волн. Генерация гармоники наиб. эффективна в условиях фазового и группового синхронизма, когда
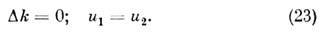
Тогда для вещественных амплитуд rl, r2 из (22) получаем (b1 = b2=b):
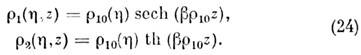
Графики решений (20), (24) представлены на рис. 4( а); видно, что при выполнении условия (23) вся энергия основной волны переходит в гармонику, реализуется накапливающееся взаимодействие; оптический удвоитель частоты обладает кпд ~ 100%. Если же расстройка Dk велика, быстро осциллирующий член в правых частях уравнений (22) практически полностью подавляет нелинейный эффект (см. также Взаимодействие световых волн).
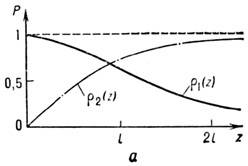
Рис. 4. Удвоение частоты света: а - пространствен ное изменение вещественных амплитуд r1, r2 в усло виях фазового синхронизма; б - схема реализации условий фазового синхронизма в двулучепреломля ющем кристалле. Приведены сечения поверхностей показателя преломления для обыкновенной n0(w) и необыкновенной ne(2w) волн.
Мелкомасштабные и крупномасштабные накапливающиеся продольные взаимодействия. Условия фазового синхронизма в оптике наиб. эффективно реализуются в двулучепреломляющих кристаллах. Имитация отсутствия дисперсии Dk = k2 -2k1= (2w/с)[ п(2w) - п(w)].= 0 возможна, если волны основной частоты и гармоники поляризованы ортогонально (рис. 4,6). Пересечение поверхностей n е(2w) и n0(w) определяет конус направлений, вдоль к-рых n е(2w) = n0(w). Пространственный масштаб накапливающегося продольного взаимодействия плоских гармонич. волн на частотах w и 2w, распространяющихся вдоль такого направления, L|| == Dk-1
 . Однако неизбежно присутствующие временная и пространственная модуляции волны приводят к ограничению величины L||. Тем не менее и в этой ситуации продольные взаимодействия удаётся сделать крупномасштабными, если L|| > L нл
. Однако неизбежно присутствующие временная и пространственная модуляции волны приводят к ограничению величины L||. Тем не менее и в этой ситуации продольные взаимодействия удаётся сделать крупномасштабными, если L|| > L нл b-1r-1(0). Здесь т. н. нелинейная длина L нл - характерное расстояние, на к-ром > 50% энергии осн. волны переходит в гармонику в условиях фазового синхронизма.
b-1r-1(0). Здесь т. н. нелинейная длина L нл - характерное расстояние, на к-ром > 50% энергии осн. волны переходит в гармонику в условиях фазового синхронизма.Крупномасштабные продольные взаимодействия удаётся реализовать в пучках мощных лазеров, макс. кпд удвоителей частоты достигают ~80-90%. Если разность n(2w) - n(w) определяется естеств. дисперсией среды, то L||
 Dn-1 не превышает 10-3 см и даже для световых полей, близких к пробойным, продольные взаимодействия остаются мелкомасштабными.
Dn-1 не превышает 10-3 см и даже для световых полей, близких к пробойным, продольные взаимодействия остаются мелкомасштабными.Управление поперечными взаимодействиями. Для эффектов, приводящих к нелинейному изменению угл. спектра, таких как самофокусировка и самодефокусировка, генерация диссипативных структур, пространственная бистабильность и мультистабильность. определяющую роль играет характерный масштаб поперечных взаимодействий L|. Мелкомасштабные поперечные взаимодействия (L| << d- поперечного размера светового пучка) возникают за счёт дифракции ("диффузии" лучевой амплитуды), диффузии частиц нелинейной среды. В системах с оптич. обратной связью, в нелинейных резонаторах ст. н. двумерной обратной связью, используя относительно несложные преобразования светового поля, можно получить L|
 d (см. раздел 7).
d (см. раздел 7).4. Сильные нелинейности, нелинейные материалы
Слабый эффект генерации 2-й оптич. гармоники был открыт в естеств. кристалле кварца. Получение кпд оптич. удвоителя частоты, достигающего десятков процентов, стало возможным только за счёт использования искусственно выращенных кристаллов, позволяющих реализовать условия синхронизма. Полтому большая величина нелинейной восприимчивости - не единств. требование к эфф. нелинейному материалу. Обычно необходима совокупность таких свойств, как нелинейность, двулучепреломление, область прозрачности, оптич. прочность и т. п. Возможности варьирования величин квадратичной нелинейной восприимчивости c(2), обусловленной быстрой электронной нелинейностью, относительно невелики. Анализ эксперим. данных позволяет сформулировать полуэмпирич. закономерность, связывающую спектральные компоненты квадратичной восприимчивости c(2) c компонентами линейной восприимчивости c(1).
Оказывается:
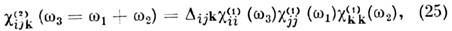
где коэф. Dijk
 10-6 СГС практически постоянен для широкого класса кристаллов. Согласно (25), оптич. материалы с высокими значениями линейного показателя преломления должны обладать и высокой квадратичной нелинейностью.
10-6 СГС практически постоянен для широкого класса кристаллов. Согласно (25), оптич. материалы с высокими значениями линейного показателя преломления должны обладать и высокой квадратичной нелинейностью.Наиб. значения c(2), полученные в кристалле Ba2NaNb5O15 в видимом диапазоне (c(2)
 10-8 СГС) и в кристалле Те в ИК-диапазоне (c(2)
10-8 СГС) и в кристалле Те в ИК-диапазоне (c(2)  2,2.10-6 СГС) ещё в 1960-х гг., практически не были превзойдены и в 1980-х гг. (табл.). Это не свидетельствует, однако, об отсутствии прогресса в разработке материалов с квадратичной нелинейностью. Наиболее яркие достижения получены в разработке нелинейных кристаллов для преобразования широкоапертурных пучков импульсных лазеров для установок УТС и в разработке кристаллов для преобразования излучения с высокой ср. мощностью. Удвоитель частоты на кристалле калий - титанил фосфата (КТР) обладает кпд
2,2.10-6 СГС) ещё в 1960-х гг., практически не были превзойдены и в 1980-х гг. (табл.). Это не свидетельствует, однако, об отсутствии прогресса в разработке материалов с квадратичной нелинейностью. Наиболее яркие достижения получены в разработке нелинейных кристаллов для преобразования широкоапертурных пучков импульсных лазеров для установок УТС и в разработке кристаллов для преобразования излучения с высокой ср. мощностью. Удвоитель частоты на кристалле калий - титанил фосфата (КТР) обладает кпд  60% при средней мощности лазерного излучения - 20 Вт.
60% при средней мощности лазерного излучения - 20 Вт.Неорганические кристаллы для нелинейнооптических преобразователей

Представление о диапазоне значений кубичной нелинейной восприимчивости в совр. нелинейных материалах даёт диаграмма рис. 3. Несмотря на разнообразие физ. механизмов нелинейности, можно чётко выделить неск. принципов, лежащих в основе поиска и разработки сильнонелинейных материалов.
Величина кубичной восприимчивости [ср. (11), (16)] определяется произведением трёх факторов - фактора, характеризующего величину матричных элементов (дипольных моментов), - D(3), вовлечённых в нелинейный процесс, их резонансного вклада R(3) и фактора локального поля L(3):
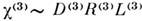 . Управление каждым из них приводит к значительным результатам в разработке материалов с кубичной нелинейностью.
. Управление каждым из них приводит к значительным результатам в разработке материалов с кубичной нелинейностью.Управлять фактором D(3) можно за счёт делокали-зации электронных состояний, ибо осн. вклад в линейную и нелинейную поляризуемости дают слабосвязанные электроны. Пример сильно делокализованных состояний - p-электроны в органич. молекулах с сопряжёнными связями. С увеличением числа сопряжённых связей - делокализацией электронов - в молекулах полимеров возрастает поляризуемость g(3) (рис. 5).
Эфф. использование резонансов, описываемых фактором R(3) (рис. 2), приводит также к получению сильных кубичных нелинейностей (напр., вблизи экситонных резонансов в полупроводниковых сверхрешётках).
Рис. 5. Зависимость гиперполяризуемости g(3)(3w) от числа двойных связей в молекулах полимеров; точки - эксперимент, сплошная линия - теория.
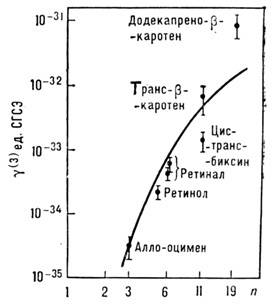
Весьма разнообразны возможности увеличения c(3) за счёт фактора локального поля. Здесь следует упомянуть легирование кристаллов и стёкол, использование кластерных систем, включая кластеры на границах раздела. На шероховатых поверхностях металлов и полупроводников действующее поле может возрастать, по крайней мере, на два порядка.
5. Нелинейная спектроскопия и нелинейная диагностика вещества
Традиционным предметом спектроскопии до появления лазеров было исследование дисперсии действительной и мнимой частей линейной восприимчивости c(1)(w)- В соответствии с этим, говоря о нелинейной спектроскопии, часто имеют в виду методы и результаты исследований частотной зависимости нелинейного отклика вещества или - для слабонелинейной среды - частотной зависимости нелинейных воспри-имчивостей. Фактически предмет и методы современной нелинейной спектроскопии шире и разнообразнее. Быстрый прогресс техники генерации коротких световых импульсов (длительностью всего в неск. световых периодов, фемтосекундные световые импульсы) привёл к разработке эфф. методов исследования нестационарного нелинейного отклика вещества на импульсное оптич. возбуждение. Эту спектроскопию, альтернативную традиционной "частотной" (frequency-domain) спектроскопии, принято называть временной (time-domain) спектроскопией. Совр. нелинейная лазерная спектроскопия включает и нелинейную спектрохроно-графию, изучающую частотную зависимость нелинейного отклика нестационарных сред; имеется в виду частотная спектроскопия с временным разрешением. Помимо информации о новых (нелинейных) параметрах вещества, нелинейная спектроскопия открывает принципиально новые возможности извлечения данных, являющихся традиц. предметом линейной спектроскопии,- данных о положении и структуре спектральных линий, сечениях рассеяния и т. п.; один из ярких примеров - свободная от доплеровского уширения двух-фотонная атомная и молекулярная спектроскопия.
Хотя нелинейная спектроскопия в принципе имеет дело с бесконечным числом новых параметров - нелинейных восприимчивостей разл. порядков c(n)(w1,..., wn), фактически в большинстве применяемых методов (когерентная активная спектроскопия рассеяния света, спектроскопия двухфотонного поглощения, нелинейная поляризац. спектроскопия) исследуются резонансы в кубичной нелинейной восприимчивости
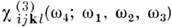 , к-рая стала одной из важнейших характеристик материальных сред.
, к-рая стала одной из важнейших характеристик материальных сред.Примером может служить когерентная спектроскопия комбинац. рассеяния света, или, как её часто называют, КАРС-спектроскопия (когерентная антистоксова рамановская спектроскопия). Подчиняющиеся альтернативному запрету комбинац. резонансы (см. Комбинационное рассеяние света )внелинейном отклике проявляются как резонансы в кубич. восприимчивости. Согласно классич. модели комбинац. рассеяния, поляризуемость молекулы
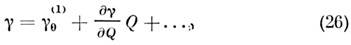
где Q- смещение ядер, для к-рого ур-ние движения имеет вид
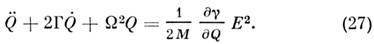
В соответствии с (26), (27) в поляризации Р появляется член, кубичный по полю. Действительно,
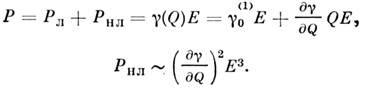
Если на среду действует бигармонич. поле вида (13), в результате четырёхфотонных взаимодействий на кубич. нелинейности возникает, в частности, волна поляризации, а следовательно, и когерентное световое поле (его когерентность определяется целиком когерент-
ностью накачки) на частоте w а= w1 + w1 - w2 = 2w1 - w2. Соответствующая кубич. восприимчивость
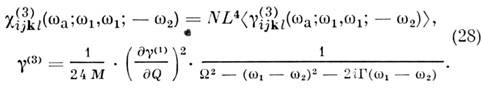
Частотная КАРС-спектроскопия основана на измерении зависимости интенсивности антистоксова сигнала (рис. 6, а)
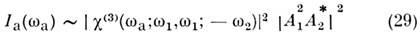
от разности частот w1 - w2. Она даёт традиц. данные о комбинационных (рамановских) резонансах; чувствительность и спектральное разрешение при этом существенно превосходят таковые для спектроскопии спонтанного комбинац. рассеяния. Вместе с тем КАРС-спектроскопия оказывается и источником принципиально новой информации, поскольку кубич. восприимчивость в (29) слагается из неск. составляющих - помимо резонансной восприимчивости cR(3), связанной с колебат. резонансом (28), вклад в антистоксов сигнал дают четырёхфотонные процессы, развивающиеся на быстрой нерезонансной электронной нелинейности cNR(3) (см. Активная лазерная спектроскопия).
Рис. 6. Схема частотной (a) и временнoй ( б) КАРС-спектроскопии комбинационных резонан сов в кубической восприимчивости g(3).
Принцип временнoй нелинейной спектроскопии комбинац. рассеяния (нестационарной КАРС-спектроско-пии) поясняет рис. 6( б). Комбинац. резонанс возбуждается двумя короткими лазерными импульсами, разность ср. частот излучения к-рых w1 -w2 ближе к частоте W. Короткий зондирующий импульс Е пр с задержкой по отношению к возбуждающим импульсам используется для измерения кинетики затухания нелинейного отклика.
Кубич. нелинейный отклик на немонохроматич. поле
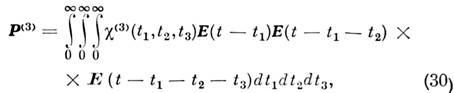
где Е = Е1 + E2 + E пр.
Измеряемая в частотной нелинейной спектроскопии спектральная компонента кубич. нелинейной восприимчивости c(3)(w а) является, очевидно, трёхмерным фурье-образом фигурирующей в (30) нелинейной ф-ции отклика
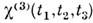 :
: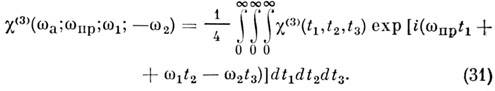
Рис. 7. Экспериментальные данные нестационарной КАРС-спектроскопии кристалла перилена, получен ные при длительности импульса t н, меньшей периода молекулярных колебаний T м.
При исследовании однородно уширенного комбинац. резонанса частотная и временная КАРС-спектроскопия представляет собой альтернативные методы извлечения данных о ширине линии Dv = Г/2p или о прямо связанном с ней времени поперечной релаксации (дефази-ровки) T2 = (Dv)-1. В частотной спектроскопии спектральное разрешение тем выше, чем больше отношение Dv/Dv л, где Dv л - ширина линии используемого лазерного излучения. Аналогичным нараметром в нестациопарной спектроскопии является отношение времени де-фазировки T2 к длительности возбуждающих и зондирующих импульсов t л: должно выполняться условие T2/t л >> 1. Если для возбуждения и зондирования во временной спектроскопии используются фемтосекунд-ные световые импульсы, то (поскольку wi/W >> 1) возможны ситуации, когда длительности пробных импульсов оказываются малыми не только по сравнению с временами релаксации энергии и фазы, но и по сравнению с Т м = 2p/W - периодом молекулярных колебаний. В этом случае появляется возможность регистрировать не только огибающую, но и саму форму молекулярных колебаний (рис. 7); нелинейный спектрометр становится стробоскопич. "оптическим осциллографом".
Регистрация нелинейного отклика используется для нелинейнооптич. диагностики кристаллич. структуры приповерхностных слоев сильно поглощающих монокристаллов полупроводников и металлов (особенно диагностики с пико- и субпикосекундным временным разрешением). Совр. эксперим. техника позволяет легко регистрировать квадратичные и кубичные по полю эффекты в отражённом от кристалла свете, нелинейные взаимодействия в тонких приповерхностных слоях.
Нелинейное отражение от кристалла кремния (рис. 8) можно использовать для диагностики нарушений кристаллич. структуры, возникающих при ионной имплантации. В основе техники регистрации лежит анизотропия нелинейного отклика (линейный отклик Si - изотропен). Из рис. 8( б, в )видно, что увеличение дозы имплантации уменьшает анизотропию в угл. распределении интенсивности квадрупольной 2-й гармоники (дипольная 2-я гармоника в Si запрещена); уменьшение анизотропии удаётся непосредственно связать с мерой аморфизации кристалла.
Рис. 8. Нелинейнооптическая диагностика поверх ности монокристалла Si: a - интенсивность 2-й гармоники, отражённой от совершенного кристалла в зависимости от угла поворота в; б, в - то же в имплантированном Si при разных дозах имплан тации D=1,2.1014 см -2 ( б), 2,4.1014 см -2 ( в).
Сильная анизотропия проявляется и в нелинейном отклике монокристаллов металлов - в Аu, Сu, Аl; зарегистрирован нелинейный отклик от плёнок, обладающих высокотемпературной сверхпроводимостью. Всё это стимулирует применение нелинейных оптич. методов к анализу динамики электронной структуры нормальных и сверхпроводящих металлов. Чувствительность нелинейного отклика к тонким деталям зонной структуры полупроводников и металлов делает нелинейнооптич. диагностику эфф. методом изучения не только симметрии потенциала, в к-ром движется электрон, но и деталей картины этого движения.
6. Параметрические процессы и параметрические преобразователи
Интенсивная световая волна - волна "накачки"
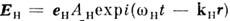 , распространяющаяся в среде с быстрым нелинейным откликом, модулирует её диэлектрич. проницаемость е по закону бегущей волны. Бегущая волна диэлектрич. проницаемости способна усиливать слабые волны с соответствующим образом подобранными частотами и волновыми векторами - эффект, имеющий ряд общих черт с парамет-рич. усилением и параметрич. генерацией в системах с сосредоточенными параметрами.
, распространяющаяся в среде с быстрым нелинейным откликом, модулирует её диэлектрич. проницаемость е по закону бегущей волны. Бегущая волна диэлектрич. проницаемости способна усиливать слабые волны с соответствующим образом подобранными частотами и волновыми векторами - эффект, имеющий ряд общих черт с парамет-рич. усилением и параметрич. генерацией в системах с сосредоточенными параметрами.В квадратичной среде диэлектрич. проницаемость
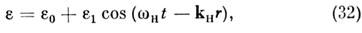
где e1 - коэф. модуляции диэлектрич. проницаемости, w н = w1 + w2 - частота накачки, равная сумме частот параметрически усиливаемых волн.
Поведение комплексных амплитуд волн, участвующих в таком трёхчастотном ("трёхфотонном") параметрич. процессе (без учёта потерь), описывается системой трёх ур-ний [ср. (22)]:
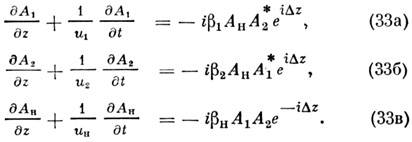
Если u1 = u2 = u н, Dz = 0 (выполняются условия фазового синхронизма kH = k1+ k2) и A1, A2 << А н . (последнее приближение обычно наз. приближением заданного поля накачки), то решения ур-ний (33а) и (33 б)
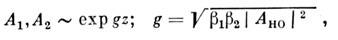
т. е. волны на частотах w1, w2 экспоненциально усиливаются. Расстройка фазовых скоростей (D
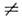 0), обусловленная дисперсией среды, снижает инкремент: g =
0), обусловленная дисперсией среды, снижает инкремент: g =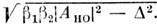 Однако увеличением интенсивности накачки в определ. мере можно скомпенсировать эффекты расфазировки.
Однако увеличением интенсивности накачки в определ. мере можно скомпенсировать эффекты расфазировки.Для немодулиров. волн при D = 0, и1 - и2 = и н система (33а) - (33в) допускает точное решение в эл-липтич. ф-циях. Графики решений представлены на рис. 9; интенсивности нормированы на интенсивность сигнальной волны на частоте w1. Пространственные биения трёх волн, изображённые на рис., представляют по существу периодич. последовательность процессов параметрич. усиления в поле мощной волны накачки w н
 w1 + w2 и сложения частот w1 + w2
w1 + w2 и сложения частот w1 + w2  w н. В кубичной среде диэлектрич. проницаемость изменяется с удвоенной частотой накачки.
w н. В кубичной среде диэлектрич. проницаемость изменяется с удвоенной частотой накачки.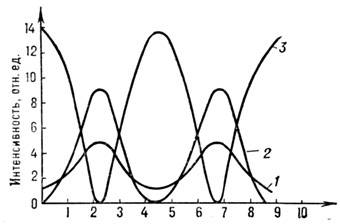
Рис. 9. Динамика изменения интенсивности волн при параметрическом взаимодействии в среде с квадратичной нелинейностью. По оси абсцисс - приведённая длина нелинейной среды; по оси ординат - интенсивности (в относительных еди ницах) волн сигнала I1/I10(1), разностной частоты I2/I10 (2) и накачки IH/I10 (3).
Коэф. модуляции диэлектрич. проницаемости e1.~ c(3) А2 н. Частота накачки связана с частотами усиливаемых волн в этом случае соотношением

(четырёхчастотный - четырёхфотонный параметрич. процесс), и накапливающиеся взаимодействия имеют место, если

Экспоненциальное усиление волн на частотах w1, w2 происходит в этом случае с инкрементом g=
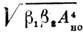 , где bi ~ c(3).
, где bi ~ c(3).Трёх- и четырёхчастотные параметрич. взаимодействия играют фундам. роль в Н. о. Трёхчастотное параметрич. усиление лежит в основе принципа действия перестраиваемых параметрических генераторов света: при фиксиров. частоте накачки w н частоты усиливаемых волн w1 и w2 можно перестраивать, изменяя дисперсионные свойства среды.
Параметрич. генератор на основе кристалла ВВО (табл.) плавно перестраивается во всём видимом и ближнем ИК-диапазоне. Четырёхчастотные параметрич. взаимодействия также могут быть положены в основу разработки нелинейнооптич. преобразователей. Вместе с тем здесь следует подчеркнуть обстоятельство более принципиального порядка. В соответствии с (34а) и (34б) частоты взаимодействующих волн могут быть весьма близки: вырожденный режим четырёх-частотного взаимодействия соответствует w н = w1 = = w2; однако волны могут различаться направлениями распространения, поляризациями. Благодаря этому для них легко реализуются крупномасштабные продольные и поперечные взаимодействия. В результате именно эффективные четырёхчастотные взаимодействия волн с близкими частотами определяют основные черты поведения мощного светового пучка в нелинейной среде - разнообразные неустойчивости, преобразования формы пространственной и временной модуляций и т. п.
7. Нелинейная динамика модулированных световых волн в кубичной среде
В среде с кубичной нелинейностью наиб. интерес представляют эффекты самовоздействия световых пакетов и пучков, обусловленные четырёхволновыми взаимодействиями разл. компонент их частотного и угл. спектров. Разнообразие механизмов нелинейности показателя преломления и возможность эфф. управления пространственными масштабами продольных L|| и поперечных L | взаимодействий (варьируя ширину спектра, интенсивность светового поля, удаётся, в отличие от квадратичных сред, изменять соотношение между нелинейностью и дисперсией) позволяют реализовать в кубичной среде разнообразнейшие эффекты нелинейной волновой динамики. В основе их лежит сравнительно небольшое число фундаментальных нелинейных эффектов. Анализ их проводят в терминах преобразования пространственно-временных огибающих; при физ. интерпретации используют и спектральные представления.
Самомодуляция, самосжатие и самофокусировка. В среде с вещественным нелинейным показателем преломления волновые пакеты и пучки испытывают фазовую самомодуляцию, к-рая за счёт дисперсии и рефракции сильно изменяет форму временной или пространственной модуляции огибающей. Для волнового пакета вида
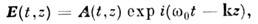
распространяющегося в среде с нелинейным показателем преломления (17), полное изменение фазы
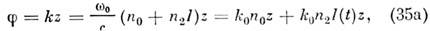
т. е. возникает зависящая от интенсивности добавка к фазе j нл (t)= -k0n2I(t)z, а следовательно, и частотная модуляция
В результате частотный спектр пакета сильно уширяется. При n2 > 0 частота увеличивается от фронта импульса к хвосту. В среде с нормальной дисперсией групповой скорости это приводит, очевидно, к более быстрому расплыванию пакета, чем в линейной среде. Если дисперсия аномальна, спектральные ВЧ-компоненты, группирующиеся на хвосте импульса, догоняют НЧ-компоненты, располагающиеся на фронте; при этом частотно-модулиров. импульс сжимается - возникает самосжатие, "самофокусировка во времени". Во многом аналогичные явления возникают и при распространении волновых пучков. Рис. 10 иллюстрирует картину распространения волнового пучка в среде с n2 > 0. Колоколообразное распределение огибающей приводит к фазовой самомодуляции в пространстве; в рассматриваемом случае n2 > 0 она приводит к нелинейной рефракции и самофокусировке пучка, т. к. фазовая скорость света в центре пучка u ф.= с/(п0 + n2I) меньше, чем на периферии. Следует подчеркнуть, что, в отличие от "линейной" фокусировки света с помощью линзы, самофокусировка носит "лавинный" характер, характер нeустойчивости. Действительно, вызванная фазовой самомодуляцией поперечная неоднородность поля усиливает нелинейную рефракцию и т. д. Самосжатие, самофокусировку можно интерпретировать и на спектральном языке как результат последовательных четырёхволно-вых взаимодействий, приводящих к "лавинному" уши-рению частотного или углового спектров.
Рис. 10. Изменения профиля светового пучка в ку бичной среде с п2.> 0, обусловленные пространствен ной фазовой самомодуляцией. Штриховые линии - изменяющаяся форма фазового фронта. Внизу - нарастание напряжённости светового поля на оси пучка.
Оптические солитоны. Чем определяется предельное нелинейное сжатие светового импульса и светового пучка? При самосжатии плоских волновых пакетов, обусловленном продольными взаимодействиями, компрессия сдерживается дисперсионным расплыванием. При этом оказывается возможным устойчивый баланс
Рис. 11. Изменение формы импульсов с расстоянием, пройденным в нелинейной среде: а - при W< W кp.- расплывание; б - при W = W кp - оптический соли- . тон; в - при W> WKp -компрессия.
сжатия и расплывания; он достигается при плотности энергии пакета (Дж/см 2)
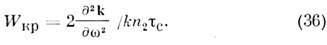
При W = W кp в кубичной среде распространяется стационарный импульс - солитон оптический, огибающая к-рого
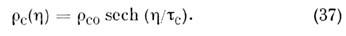
Такой импульс является стационарным решением нелинейного параболич. ур-ния типа (21)
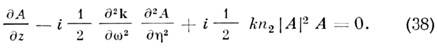
Изменение формы световых импульсов при разл. соотношениях между W и W кp изображено на рис. 11. Существенным оказывается то, что солитонное решение вида (37) оказывается устойчивым по отношению к малым вариациям W вблизи W кp.
Нелинейная рефракция, приводящая к пространственной самофокусировке света, сдерживается дифракцией. Баланс нелинейной рефракции и дифракции достигается при полной мощности трёхмерного пучка

[ср. с (36)]. Для волнового пакета и двумерного пучка баланс определяется интенсивностью, для трёхмерного - полной мощностью. Однако здесь баланс неустойчив; при Р> Р кр нелинейная рефракция подавляет дифракцию, пучок продолжает сжиматься. Пределом этого "лавинного" процесса часто становится оптический пробой (см. также Самофокусировка света).
Оптическая бистабильность. Эффективность продольных взаимодействий может быть резко усилена за счёт использования обратной связи, оптич. резонатора. Ярким примером такого усиления является возникновение амплитудной оптич. бистабильности в оптич. резонаторе Фабри - Перо, заполненном средой с кубичной нелинейностью. За счёт многократного прохождения через среду сигнал на выходе приобретает значительный нелинейный фазовый набег. При достаточно большой интенсивности на входе интенсивность на выходе испытывает скачки и обнаруживает гистерезис (подробнее см. Оптическая бистабильность).
Генерация пространственных структур, оптическая турбулентность. Обусловленные продольными взаимодействиями оптич. бистабильность и соответствующие неустойчивости являются лишь "временными" проекциями широкого класса волновых взаимодействий, происходящих одновременно в пространстве и времени. Принципиальную роль здесь играют поперечные взаимодействия, к-рые в свободно распространяющихся пучках и в традиц. схемах оптич. резонаторов имеют характер диффузии и оказываются мелкомасштабными. Пространственным масштабом и топологией поперечных взаимодействий можно управлять в системах с двумерной обратной связью (рис. 12). В цепь обратной связи кольцевого оптич. резонатора помещается трансформатор поля, осуществляющий поворот, сжатие, растяжение, благодаря чему удаётся получить L | ~ ~d (d - диаметр пучка]. В четырёхзеркальном кольцевом резонаторе оказываются связанными между собой поля в разл. точках поперечного сечения пучка. Если в такой резонатор поместить среду с нелинейным показателем преломления, гистерезис и бистабильность возникают не только во времени, но и в пространстве.
Рис. 12. Оптический резонатор с двумерной обратной связью: 1 -нелинейная среда; a - трансформатор поля.
Нелинейная динамика поля в резонаторе с двумерной обратной связью описывается ур-нием для нелинейного фазового набега j(r,t):
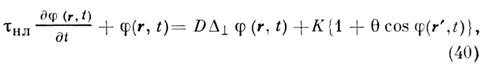
где
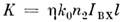 - "управляющий параметр" l- длина нелинейной среды, h - параметр потерь, q - видность интерференц. картины.
- "управляющий параметр" l- длина нелинейной среды, h - параметр потерь, q - видность интерференц. картины. 
Рис. 13. Нелинейные структуры в резонаторе с дву мерной обратной связью: а, б - вращающиеся волны; в, г - спиральные волны (случаю г соответствует меньший коэффициент диффузии); д - сосуществова ние вращающейся и спиральной структур; е - опти ческая турбулентность.
Поперечные взаимодействия описываются правой частью (40), первый член характеризует мелкомасштабные взаимодействия; крупномасштабным взаимодействиям обязан сдвиг аргумента cos, r'
 r (параболич. ур-ние со сдвинутым аргументом). На рис. 13 приведены фотографии наиб. типичных нелинейных структур: вращающихся волн (оптич. ревербераторов); спиральных волн, возникающих при больших значениях параметра К; случайных нелинейных полей - оптич. турбулентности. Т. о., в Н. о. воспроизводится полный набор явлений нелинейной волновой динамики, интенсивно исследуемых в гидродинамике, физике плазмы, биологии и т. д. (см. также Волны).
r (параболич. ур-ние со сдвинутым аргументом). На рис. 13 приведены фотографии наиб. типичных нелинейных структур: вращающихся волн (оптич. ревербераторов); спиральных волн, возникающих при больших значениях параметра К; случайных нелинейных полей - оптич. турбулентности. Т. о., в Н. о. воспроизводится полный набор явлений нелинейной волновой динамики, интенсивно исследуемых в гидродинамике, физике плазмы, биологии и т. д. (см. также Волны).8. Рассеяние на оптически индуцированных когерентных элементарных возбуждениях - вынужденное рассеяние
Важным классом нелинейных оптич. эффектов являются процессы вынужденного рассеяния (ВР), в к-рых мощная световая волна индуцирует когерентные элементарные возбуждения в среде (оптич. и акустич. фо-ноны, поляритоны, температурные волны и т. п.) и когерентно рассеивается на них. Каждому виду спонтанного рассеяния света соответствует вынужденный аналог (см. Вынужденное рассеяние света, Комбинационное рассеяние света).
Вынужденное комбинац. рассеяние (ВКР) происходит на когерентно возбуждённых оптич. фононах. Для классич. описания процесса ВКР используют модель нелинейно связанных осцилляторов. Обозначим через х нормальную координату колебаний атомов в молекуле изотропной среды, а через у - нормальную координату колебаний "оптических" электронов. В линейном приближении колебания атомов и определяющие поляризацию среды колебания электронов совершаются независимо друг от друга. При учёте нелинейной связи потенц. энергию молекулы можно представить в виде
где F и f - "упругости" связей в молекуле. Член a ху2. описывает взаимодействие электронных и колебательных возмущений в молекуле (электрон-фононные взаимодействия). С учётом этого члена ур-ния движения для х и у приобретают вид [ср. с простой моделью ангармонич. осциллятора (4)]:
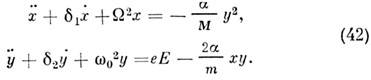
Здесь М и m - приведённые массы атомного и электронного осцилляторов, W - частота молекулярных колебаний, е - заряд электрона, Е - электрич. поле световых волн. Если на систему, описываемую (42), действует бигармонич. поле (13) с частотами w1. и w2, то при w1 - w2
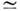 W. будет происходить резонансная раскачка молекулярных колебаний. Этот процесс используется в когерентной антистоксовой спектроскопии (см. раздел 5) [систему (42) можно рассматривать как классич. обоснование феноменологич. ур-ния (27)]. Теперь, однако, гл. акцент делается на обусловленном комбинац. резонансом энергообмене волн с частотами w1 и w2. Энергия ВЧ-волны накачки w1 = w н передаётся низкочастотной, стоксовой w2 = w с волне; при достаточно большой интенсивности накачки I н стоксова волна нарастает экспоненциально - возникает вынужденное комбинац. рассеяние
W. будет происходить резонансная раскачка молекулярных колебаний. Этот процесс используется в когерентной антистоксовой спектроскопии (см. раздел 5) [систему (42) можно рассматривать как классич. обоснование феноменологич. ур-ния (27)]. Теперь, однако, гл. акцент делается на обусловленном комбинац. резонансом энергообмене волн с частотами w1 и w2. Энергия ВЧ-волны накачки w1 = w н передаётся низкочастотной, стоксовой w2 = w с волне; при достаточно большой интенсивности накачки I н стоксова волна нарастает экспоненциально - возникает вынужденное комбинац. рассеяние 
где z - длина нелинейной среды, g - удельный коэф. усиления:

(N - число молекул в единице объёма, n н и n с - показатели преломления среды на частотах накачки и сток-совой компоненты). Типичное значение g для наиб. важных комбинационно-активных сред (сжатый водород, жидкий азот, кристалл кальцита и др.) составляет 10-9-10-8 см/Вт.
Вынужденное рассеяние используется для управления параметрами лазерного излучения: преобразования частоты, длительности, когерентности. Напр., комбинационные лазеры на сжатом водороде и жидком азоте осуществляют ВКР-преобразование лазерного излучения с квантовой эффективностью до 90%. При ВР возможна эфф. компрессия лазерных импульсов с одноврем. повышением их пиковой мощности. Практически таким способом удаётся сжимать импульсы в 10-20 раз.
Процесс ВР используется для обращения волнового фронта. При ВКР энергия частично когерентного лазерного излучения преобразуется в энергию полностью когерентного светового пучка на смещённой (стоксовой) частоте (ВКР-коррекция волнового фронта). Такая коррекция позволяет здачительно (в > 102 раз) уменьшить угл. расходимость излучения. При этом квантовая эффективность преобразования составляет обычно 30-50%, а иногда и 80-90%.
9. Статистическая нелинейная оптика. Классические и квантовые сжатые состояния световых полей
Нелинейные преобразования коренным образом изменяют статистику поля. Это хорошо известно в ста-тистич. радиофизике и в полной мере проявляется в оптике. Статистич. свойства сформированного в установившемся режиме лазерного излучения радикально отличаются от свойств гауссовского теплового излучения. С существ. изменением статистики приходится сталкиваться при генерации оптич. гармоник и комбинац. частот, в разнообразных самовоздействиях. Многие из перечисленных эффектов имеют по существу классич. природу, квантовый характер света в них не проявляется. Тем больший интерес представляет формирование с помощью нелинейных преобразований новых квантовых состояний светового поля, новых макроскопич. квантовых состояний. Наиб. яркий пример - генерация т. н. сжатых состояний поля, возникающая при параметрич. взаимодействиях. В 60-х гг. они были исследованы для классич. полей, в 80-х гг. выяснено, что они могут реализоваться и для квантованных полей. При этом возникают нетривиальные возможности управления квантовыми флуктуациями светового поля.
Классические сжатые состояния. Рассмотрим преобразование классич. шумового поля вырожденным оптич. параметрич. усилителем (w1 = w2 = w н/2). В приближении заданного поля монохроматич. накачки и D = 0 поведение фазы сигнальной волны j = argAc подчиняется ур-нию
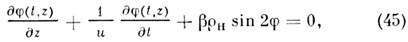
фаза волны накачки j н принята равной p/2 [(45) можно получить из (33), полагая А1=А2= А с=r с е ij]. Согласно (45):
[j0(t) - значение фазы на входе нелинейной среды], из чего следует, что на достаточно больших длинах z возможны два устойчивых состояния фазы, равных 0 и p. Если сигнальная волна представляет собой стационарный гауссов шум, то на входе параметрического усилителя w(j) = 1/2p; - p <=j <=p. По мере параметрич. усиления ф-ция распределения фазы трансформируется (рис. 14,a; кривые 1 и 2). Максимумы плотности вероятности фазы формируются вблизи устойчивых значений (0 и bp). Дисперсия флуктуации уменьшается - формируются классич. сжатые состояния поля.
Формирование сжатых состояний можно рассмотреть и в терминах поведения квадратурных компонент x(t,z )и y(t,z )сигнала:
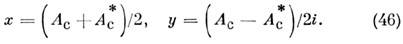
Тогда в соответствии с (33) эволюция квадратур х, у даётся соотношениями
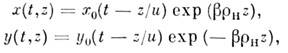
т. е. усиливается синфазная квадратура х, а противофазная у - подавляется. Для стационарного гауссова шума с дисперсией s2 дисперсии квадратур изменяются как
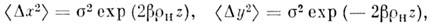
т. е. флуктуации квадратурных компонент при параметрич. усилении сигнала становятся неодинаковыми (рис. 14, б).
Рис. 14. Классический шумовой сигнал при пара метрическом усилении: а - плотность вероятности распределения фазы обычного стационарного шума (штриховая линия) и шума при сжатом состоянии (кривые 1 и 2, для 2 коэф. усиления больше); б - области флуктуации на фазовой плоскости обычного (слева) и сжатого (справа) шума.
Аналогично ведут себя при параметрич. усилении квантовые вакуумные флуктуации в поле интенсивной классич. накачки. В квантовом сжатом состоянии вакуумные флуктуации одной из квадратурных компонент оказываются подавленными, а флуктуации другой увеличиваются. Естественно, при этом должно удовлетворяться соотношение неопределённостей. Если при измерениях система реагирует лишь на одну квадратуру, шум фотодетектирования оказывается ниже уровня дробового шума. Подробнее см. Сжатое состояние.
10. Нелинейный отклик в физике воздействия лазерного излучения на вещество
Нелинейный отклик среды играет важную, а часто и решающую роль в механизмах лазерного возбуждения и релаксации сильнонеравновесных состояний в атомах, молекулах и конденсиров. средах. Первой яркой демонстрацией этого стало открытие и практич. использование селективного многофотонного возбуждения и многофотонной диссоциации молекул в сильном лазерном ИК-поле. Оказалось, что молекула может быть сильно возбуждена и затем диссоциирована при резонансном поглощении десятков фотонов из лазерного ИК-импульса интенсивностью ~ 10 МВт/см 2 и плотностью энергии ~ неск. Дж/см 2 (см. Инфракрасная многофотонная диссоциация). Этот процесс сильно влияет на хим. реакции; будучи селективной по частоте, многофотонная диссоциация в ИК-поле может быть использована для лазерного изотопов разделения.
Др. важный пример - своеобразные нелинейные самовоздействия волн на поверхности металлов и полупроводников, приводящие к возникновению периодич. поверхностных структур (рис. 15). Возникают они самопроизвольно, когда интенсивность лазерного излучения оказывается достаточно высокой; это связано с пространственно неоднородным нагревом поверхности. Необходимое для этого неоднородное поле является результатом интерференции падающей лазерной волны с полем поверхностной волны. При этом важную роль играет появляющаяся обратная связь, когда образовавшиеся периодич. структуры существенно влияют на условия рассеяния лазерного излучения в дифрагиров. волны - возникают явления, имеющие много общего с вынужденным рассеянием. В разл. условиях могут возникать неустойчивости поверхностних акустических волн, капиллярных волн в расплавах и жидких металлах и интерференц. неустойчивость испарения поверхности. Создаваемый лазерным излучением рельеф может кардинально менять поглощат. и отражат. свойства поверхности: подавлять зеркальное отражение эл.-магн. волны, приводить к резкому возрастанию (до 100%) энерговвода лазерного излучения в среду и т. п.

Рис. 15. Характерные периодические структуры, наво димые лазерным излучением на поверхности твёрдых тел: а - одномерная решётка на поверхности Ge, наво димая излучением неодимового лазера; б - двумерная решётка, возникающая на поверхности при увеличении интенсивности лазера.
11. Быстрое управление фазой и генерация фемто-секундных лазерных импульсов
Нелинейные оптич. методы быстрого управления фазой и техника компрессии сверхкоротких импульсов (техника фокусировки во времени) сыграли важную роль в получении предельно коротких, фемтосекунд-ных (длительностью ~10-15 с) световых импульсов. В основе методов лежит явление фазовой самомодуляции, приводящее к уширению спектра импульсов [см. ф-лы (35а) и (35 б)]. Для компрессии таких импульсов в случае n2 > 0 необходима среда с аномальной дисперсией групповой скорости: макс. коэф. сжатия им-пульса [см. (35б)]
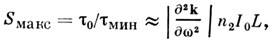
где t мин - мин. длительность импульса при компрессии. В качестве сред с аномальной дисперсией могут быть использованы пары металлов (в области частот вблизи однофотонного резонанса), устройства, состоящие из двух дифракц. решёток, нек-рые типы интерферометров. Оптимальной нелинейной средой для получения фазовой самомодуляции оказываются одномо-довые волоконные световоды. Малость нелинейности (для кварцевого волокна n2 = 3,2.10-13 см 2/кВт) с избытком компенсируется возможностью поддержания устойчивого поперечного профиля пучка диам. 5- 10 мкм на расстояниях порядка длины поглощения l п
 d-1 (в видимом диапазоне l п = 104-105 см). Оптич. компрессор, состоящий из волновода с нормальной дисперсией и двух дифракц. решёток, позволяет получить S
d-1 (в видимом диапазоне l п = 104-105 см). Оптич. компрессор, состоящий из волновода с нормальной дисперсией и двух дифракц. решёток, позволяет получить S  102. Существ. сжатия могут быть получены и при генерации оптич. солитонов.
102. Существ. сжатия могут быть получены и при генерации оптич. солитонов.12. Обработка информации и оптические компьютеры
Быстро развивающаяся область приложения методов Н. о.- разработка новых систем оптической обработки информации, создание оптич. цифровых и аналоговых процессоров.
В основу создания быстродействующих двоичных оптич. триггеров для цифрового оптич. процессора может быть положена амплитудная оптич. бистабиль-ность. С практич. точки зрения наиб. впечатляющ прогресс в технологии амплитудных оптич. триггеров на полупроводниковых микрорезонаторах. На риc. 16 показана ячейка бистабильных оптич. микрорезонаторов на GaAs - AlAs-сверхрешётках. Логич. устройство "или" па таких микрорезонаторах переключается с помощью светового импульса с энергией W п
 2•10-11 Дж. Характерное время переключения составляет t п
2•10-11 Дж. Характерное время переключения составляет t п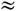 10-10 с.
10-10 с.
Рис. 16. Ячейка оптических бистабильных микро резонаторов GaAs - элемент процессора пол ностью оптического компьютера. Характерный размер ~ 2 мкм.
При дальнейшем совершенствовании технологии можно ожидать значений W п
 2.10-15 Дж (величина, в 30 раз превышающая флуктуац. предел) и t п
2.10-15 Дж (величина, в 30 раз превышающая флуктуац. предел) и t п  5.10-12 с. Перспективы использования методов Н. о. и лазерной физики в технике оптич. компьютеров не исчерпываются амплитудными триггерами. Совр. Н. о. позволяет создавать быстродействующие амплитудные, фазовые и поляризац. оптич. триггеры, оперирующие не только с дискретными сигналами, но и с волновыми структурами. Перспективно использование методов Н. о. для создания нейронно-сетевых компьютеров, предназначенных для решения нерегулярных задач, распознавания образов, моделирования интеллекта. Здесь можно использовать системы обращения волнового фронта, матрицы нелинейных переключающих элементов в совокупности с голографич. преобразователями и анализаторами световых полей. Др. возможностью оптич. моделирования системы нейронов, сложным образом связанных между собой, является развитие идеи двумерной обратной связи в кольцевом нелинейном резонаторе (рис. 12, 13). В таком резонаторе на смену обычной амплитудной оптич. би-стабильности приходят новые нелинейные волновые явления, сопровождающиеся возникновением разнообразных пространственных структур, к-рые могут быть использованы в аналоговых процессорах, системах ассоциативной памяти (см. Оптические компьютеры). Использование методов Н. о. расширяет возможности молекулярной электроники. Большие органич. молекулы обладают сильным кубич. откликом; особый интерес, с этой точки зрения, представляет отклик сильно-делокализов. электронов (рис. 5). Резкого дополнит. увеличения кубич. восприимчивости c(3) (в 104-105 раз) можно добиться, переводя молекулу в возбуждённое электронное состояние. Это обстоятельство можно использовать для записи и считывания информации. Комбинирование методов Н. о. с методами молекулярной электроники может открыть совершенно неожиданные перспективы в разработке компьютеров новых поколений.
5.10-12 с. Перспективы использования методов Н. о. и лазерной физики в технике оптич. компьютеров не исчерпываются амплитудными триггерами. Совр. Н. о. позволяет создавать быстродействующие амплитудные, фазовые и поляризац. оптич. триггеры, оперирующие не только с дискретными сигналами, но и с волновыми структурами. Перспективно использование методов Н. о. для создания нейронно-сетевых компьютеров, предназначенных для решения нерегулярных задач, распознавания образов, моделирования интеллекта. Здесь можно использовать системы обращения волнового фронта, матрицы нелинейных переключающих элементов в совокупности с голографич. преобразователями и анализаторами световых полей. Др. возможностью оптич. моделирования системы нейронов, сложным образом связанных между собой, является развитие идеи двумерной обратной связи в кольцевом нелинейном резонаторе (рис. 12, 13). В таком резонаторе на смену обычной амплитудной оптич. би-стабильности приходят новые нелинейные волновые явления, сопровождающиеся возникновением разнообразных пространственных структур, к-рые могут быть использованы в аналоговых процессорах, системах ассоциативной памяти (см. Оптические компьютеры). Использование методов Н. о. расширяет возможности молекулярной электроники. Большие органич. молекулы обладают сильным кубич. откликом; особый интерес, с этой точки зрения, представляет отклик сильно-делокализов. электронов (рис. 5). Резкого дополнит. увеличения кубич. восприимчивости c(3) (в 104-105 раз) можно добиться, переводя молекулу в возбуждённое электронное состояние. Это обстоятельство можно использовать для записи и считывания информации. Комбинирование методов Н. о. с методами молекулярной электроники может открыть совершенно неожиданные перспективы в разработке компьютеров новых поколений.Лит.: Ахманов С. А., Хохлов Р. В., Проблемы нелинейной оптики, М., 1964; Бломберген Н., Нелинейная оптика, пер. с англ., М., 1966; Клышко Д. Н., Фотоны и нелинейная оптика, М., 1980; Ахманов С. А., Коро-теев Н. И., Методы нелинейной оптики в спектроскопии рассеяния света, М., 1981; Райнтжес Дж., Нелинейные оптические параметрические процессы в жидкостях и газах, пер. с англ., М., 1987; Летохов В. С., Нелинейные селективные фотопроцессы в атомах и молекулах, М., 1983; Зельдович Б. Я., Пилипецкий Н. Ф., Шкунов В. В., Обращение волнового фронта, М., 1985; Ахманов С. А., Выслоух В. А., Чиркин А. С., Оптика фемтосекунд-ных лазерных импульсов, М., 1988; Шен И. Р., Принципы нелинейной оптики, пер. с англ., М., 1989; Летохов В. С., Чеботаев В. П., Нелинейная лазерная спектроскопия, М., 1989; Гиббс X., Оптическая бистабильность, управление светом с помощью света, пер. с англ., М., 1988; Новые физические принципы оптической обработки информации, под ред. С. А. Ахманова и М. А. Воронцова, М., 1990. С. А. Ахманов.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
