Математические символы

В математике повсеместно используются символы для упрощения и сокращения текста. Ниже приведён список наиболее часто встречающихся математических обозначений, соответствующие команды в

Кроме указанных символов, иногда используются их зеркальные отражения, например, 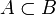$A \subset B$ обозначает то же, что и $B \supset A$.

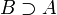Символ (Символ (Unicode)	Название	Значение	Пример
	Произношение
	Раздел математики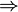
$\Rightarrow\,$	⇒	Импликация, следование	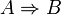$A \Rightarrow B\,$ означает «если A верно, то B также верно». Иногда вместо него используют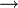 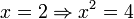$\rightarrow\,$.	$x = 2 \Rightarrow x^2 = 4\,$ верно, но 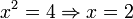$x^2 = 4 \Rightarrow x = 2\,$ неверно (так как x = − 2 также является решением).
		«влечёт» или «если…, то»
		везде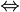
$\Leftrightarrow$	⇔	Равносильность	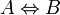$A \Leftrightarrow B$ означает «A верно тогда и только тогда, когда B верно».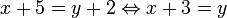	$x + 5 = y + 2 \Leftrightarrow x + 3 = y\,$
		«если и только если» или «равносильно»
		везде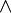
$\wedge$	∧	Конъюнкция	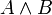$A \wedge B$ истинно тогда и только тогда, когда A и B оба истинны.	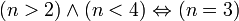$(n>2)\wedge (n<4)\Leftrightarrow (n=3)$, если n — натуральное число.
		«и»
		Математическая логика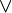
$\vee$	∨	Дизъюнкция	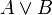$A\vee B$ истинно, когда хотя бы одно из условий A и B истинно.	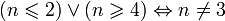$(n\leqslant 2)\vee (n\geqslant 4)\Leftrightarrow n\ne 3$, если n — натуральное число.
		«или»
		Математическая логика
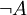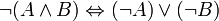
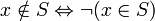
$\neg$	¬	Отрицание	$\neg A$ истинно тогда и только тогда, когда ложно A.	$\neg (A\wedge B)\Leftrightarrow (\neg A)\vee (\neg B)$ $x\notin S\Leftrightarrow \neg(x\in S)$
		«не»
		Математическая логика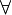
$\forall$	∀	Квантор всеобщности	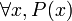$\forall x, P(x)$ обозначает «P(x) верно для всех x».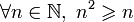	$\forall n\in \mathbb N,\;n^2\geqslant n$
		«Для любых», «Для всех»
		Математическая логика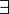
$\exists$	∃	Квантор существования	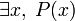$\exists x,\;P(x)$ означает «существует хотя бы один x такой, что верно P(x)»	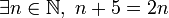$\exists n\in \mathbb N,\;n+5=2n$ (подходит число 5)
		«существует»
		Математическая логика
$=\,$	=	Равенство	x = y обозначает «x и y обозначают один и тот же объект».	1 + 2 = 6 − 3
		«равно»
		везде
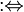
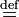
: = $:\Leftrightarrow$ $\stackrel{\rm{def}}{=}$	:= :⇔	Определение	x: = y означает «x по определению равен y». 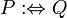$P :\Leftrightarrow Q$ означает «P по определению равносильно Q»	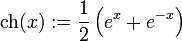${\rm ch} (x) := {1\over 2}\left(e^x+e^{-x}\right)$ (Гиперболический косинус) 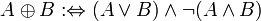$A \oplus B :\Leftrightarrow (A\vee B)\wedge \neg (A\wedge B)$ (Исключающее или)
		«равно/равносильно по определению»
		везде
{,}	{ , }	Множество элементов	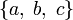$\{a,\;b,\;c\}$ означает множество, элементами которого являются a, b и c.	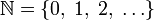$\mathbb N = \{0,\;1,\;2,\;\ldots \}$ (множество натуральных чисел)
		«Множество…»
		Теория множеств
{ | } {:}	{ | } { : }	Множество элементов, удовлетворяющих условию	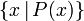$\{x\,|\,P(x)\}$ означает множество всех x таких, что верно P(x).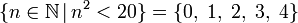	$\{n\in \mathbb N\,|\,n^2<20\} = \{0,\;1,\;2,\;3,\;4\}$
		«Множество всех… таких, что верно…»
		Теория множеств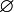
$\varnothing$ {}	∅ {}	Пустое множество	{} и 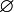$\varnothing$ означают множество, не содержащее ни одного элемента.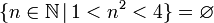	$\{n\in \mathbb N\,|\,1<n^2<4\} = \varnothing$
		«Пустое множество»
		Теория множеств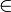
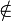
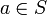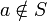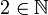
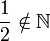
$\in$ $\notin$	∈ ∉	Принадлежность/непринадлежность к множеству	$a\in S$ означает «a является элементом множества S» $a\notin S$ означает «a не является элементом множества S»	$2\in \mathbb N$ ${1\over 2}\notin \mathbb N$
		«принадлежит», «из» «не принадлежит»
		Теория множеств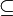
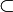
$\subseteq$ $\subset$	⊆ ⊂	Подмножество	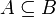$A\subseteq B$ означает «каждый элемент из A также являестя элементом из B». 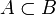$A\subset B$ обычно означает то же, что и 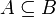$A\subseteq B$. Однако некоторые авторы используют 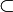$\subset$, чтобы показать строгое включение (то есть $\subsetneq$).	$(A\cap B) \subseteq A$ $\mathbb Q\subseteq \mathbb R$
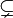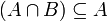
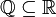
		«является подмножеством», «включено в»
		Теория множеств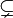
$\subsetneq$	⫋	Собственное подмножество	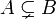$A\subsetneq B$ означает 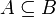$A\subseteq B$ и $A\ne B$.	$\mathbb N\subsetneq \mathbb Q$
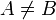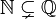
		«является собственным подмножеством», «строго включается в»
		Теория множеств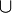
$\cup$	∪	Объединение	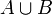$A\cup B$ означает множество элементов, принадлежащих A или B (или обоим сразу).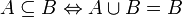	$A\subseteq B\Leftrightarrow A\cup B=B$
		«Объединение … и …», «…, объединённое с …»
		Теория множеств
$\cap$	⋂	Пересечение	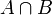$A\cap B$ означает множество элементов, принадлежащих и A, и B.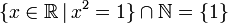	$\{x\in \R\,|\,x^2=1\}\cap \mathbb N = \{1\}$
		«Пересечение … и … », «…, пересечённое с …»
		Теория множеств
$\setminus$	\	Разность множеств	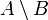$A\setminus B$ означает множество элементов, принадлежащих A, но не принадлежащих B.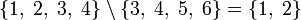	$\{1,\;2,\;3,\;4\}\setminus \{3,\;4,\;5,\;6\} = \{1,\;2\}$
		«разность … и … », «минус», «… без …»
		Теория множеств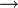
$\to$	→	Функция	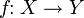$f\!\!:X\to Y$ означает функцию f с областью определения X и областью прибытия Y.	Функция 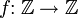$f\!\!:\mathbb Z\to \mathbb Z$, определённая как f(x) = x2
		«из … в»,
		везде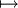
$\mapsto$	↦	Отображение	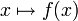$x \mapsto f(x)$ означает, что образом x после применения функции f будет f(x).	Функцию, определённую как f(x) = x2, можно записать так: 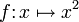$f\colon x \mapsto x^2$
		«отображается в»
		везде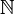
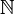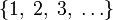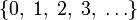$\mathbb N$	N или ℕ	Натуральные числа	$\mathbb N$ означает множество $\{1,\;2,\;3,\;\ldots\}$ или $\{0,\;1,\;2,\;3,\;\ldots\}$ (в зависимости от ситуации).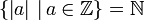	$\{\left|a\right|\,|\,a\in \mathbb Z\}=\mathbb N$
		«Эн»
		Числа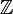
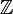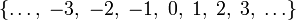
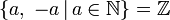
$\mathbb Z$	Z или ℤ	Целые числа	$\mathbb Z$ означает множество $\{\ldots,\;-3,\;-2,\;-1,\;0,\;1,\;2,\;3,\;\ldots\}$	$\{a,\;-a\,|\,a\in\mathbb N\}=\mathbb Z$
		«Зед»
		Числа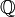
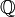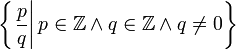
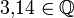
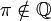
$\mathbb Q$	Q или ℚ	Рациональные числа	$\mathbb Q$ означает $\left\{\left.{p\over q} \right| p\in \mathbb Z \wedge q\in \mathbb Z\wedge q\ne 0\right\}$	$3,\!14\in \mathbb Q$ $\pi \notin \mathbb Q$
		«Ку»
		Числа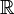
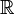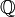
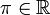
$\mathbb R$	R или ℝ	Вещественные числа, или действительные числа	$\R$ означает множество всех пределов последовательностей из 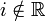$\mathbb Q$	$\pi \in \R$ $i \notin \R$ (i — комплексное число: i2 = − 1)
		«Эр»
		Числа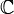
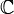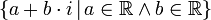
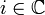
$\mathbb C$	C или ℂ	Комплексные числа	$\mathbb C$ означает множество $\{a+b\cdot i\,|\,a\in \R \wedge b\in \R\}$	$i\in \mathbb C$
		«Це»
		Числа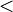
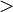
$&amp;lt;\,$ $&amp;gt;\,$	< >	Сравнение	x < y обозначает, что x строго меньше y. x > y означает, что x строго больше y.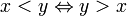	$x&amp;lt;y\Leftrightarrow y&amp;gt;x$
		«меньше чем», «больше чем»
		Отношение порядка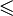
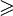
$\leqslant$ $\geqslant$	≤ или ⩽ ≥ или ⩾	Сравнение	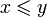$x\leqslant y$ означает, что x меньше или равен y. 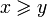$x\geqslant y$ означает, что x больше или равен y.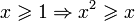	$x\geqslant 1\Rightarrow x^2\geqslant x$
		«меньше или равно»; «больше или равно»
		Отношение порядка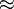
$\approx$	≈	Приблизительное равенство	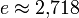$e\approx 2,\!718$ с точностью до 10 − 3 означает, что 2,718 отличается от e не больше чем на 10 − 3.	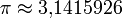$\pi \approx 3,\!1415926$ с точностью до 10 − 7.
		«приблизительно равно»
		Числа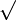
$\sqrt{ }$	√	Арифметический квадратный корень	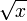$\sqrt x$ означает положительное действительное число, которое в квадрате даёт x.	$\sqrt 4=2$ $\sqrt {x^2}= \left|x\right|$
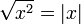
		«Корень квадратный из …»
		Числа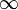
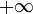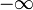$\infty$	∞	Бесконечность	$+\infty$ и $-\infty$ суть элементы расширенного множества действительных чисел. Эти символы обозначают числа, меньшее/большее всех действительных чисел.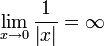	$\lim\limits_{x\to 0} {1\over \left|x\right|}= \infty$
		«Плюс/минус бесконечность»
		Числа
$\left|\;\right|$	| |	Модуль числа (абсолютное значение), модуль комплексного числа или мощность множества	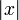$\left|x\right|$ обозначает абсолютную величину x. | A | обозначает мощность множества A и равняется, если A конечно, числу элементов A.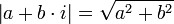	$\left|a+b\cdot i\right|=\sqrt {a^2+b^2}$
		«Модуль»; «Мощность»
		Числа и Теория множеств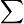
$\sum$	∑	Сумма, сумма ряда	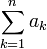$\sum_{k=1}^n a_k$ означает «сумма ak, где k принимает значения от 1 до n», то есть 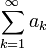$a_1+a_2+\ldots+a_n$. $\sum_{k=1}^{\infty} a_k$ означает сумму ряда, состоящего из ak.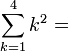	$\sum_{k=1}^4 k^2=$ = 12 + 22 + 32 + 42 = 30
		«Сумма … по … от … до …»
		Арифметика, Математический анализ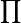
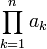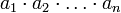
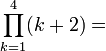
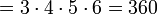
$\prod$	∏	Произведение	$\prod_{k=1}^n a_k$ означает «произведение ak для всех k от 1 до n», то есть $a_1\cdot a_2\cdot\ldots\cdot a_n$	$\prod_{k=1}^4 (k+2)=$ $=3\cdot 4\cdot 5\cdot 6=360$
		«Произведение … по … от … до …»
		Арифметика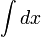
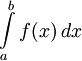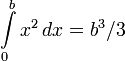
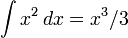
$\int dx$	∫	Интеграл	$\int\limits_a^b f(x)\, dx$ означает «интеграл от a до b функции f от x по переменной x».	$\int\limits_0^b x^2\, dx = b^3/3$ $\int x^2\, dx = x^3/3$
		«Интеграл (от … до …) функции … по (или d)…»
		Математический анализ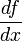
$\frac{df}{dx}$ f'(x)	df/dx f'(x)	Производная	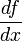$\frac{df}{dx}$ или f'(x) означает «(первая) производная функции f от x по переменной x».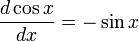	$\frac{d \cos x}{dx} = -\sin x$
		«Производная … по …»
		Математический анализ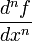
$\frac{d^n f}{dx^n}$ f(n)(x)	dnf / dxn f(n)(x)	Производная n-го порядка	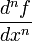$\frac{d^n f}{dx^n}$ или f(n)(x) (во втором случае если n — фиксированное число, то оно пишется римскими цифрами) означает «n-я производная функции f от x по переменной x».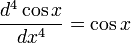	$\frac{d^4 \cos x}{dx^4} = \cos x$
		«n-я производная … по …»
		Математический анализ

См. также

• Tаблица обозначений абстрактной алгебры
• История математических обозначений