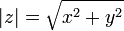- Модуль числа
-
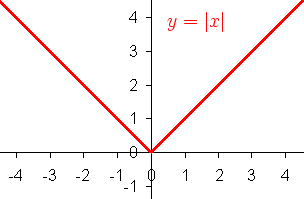
Абсолю́тная величина́ или мо́дуль вещественного или комплексного числа x есть расстояние от x до начала координат.
Более точно:
- Абсолютная величина вещественного числа x есть неотрицательное число, обозначаемое |x| и определяемое следующим образом:
- если
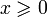 , то | x | = x;
, то | x | = x; - если x < 0, то | x | = − x.
- если
- Абсолютная величина комплексного числа z = x + iy (x и y — вещественные числа) — неотрицательное число, обозначаемое |z| и определяемое по формуле:
Модуль относится к числу элементарных функций. В математике широко используется тот факт, что геометрически | x1 − x2 | равно расстоянию между точками x1 и x2 и, таким образом, может быть использовано как мера близости одной величины к другой.
Содержание
Свойства
Для абсолютной величины имеют место следующие соотношения:
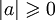 , причём | a | = 0 только если a = 0.
, причём | a | = 0 только если a = 0.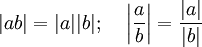 .
.- | ak | = | a | k если ak определено.
- Неравенство треугольника:
- |a + b| ≤ |a| + |b| или
- |a − b| ≥ ||a| − |b||
Альтернативные определения
Для вещественных чисел модуль можно определить и другим способом:
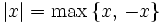 , то есть модуль числа
, то есть модуль числа 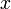 есть максимальное из двух чисел
есть максимальное из двух чисел 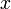 и
и 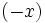 ,
,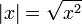 .
.
История
Считают, что термин предложил использовать Котс, ученик Ньютона. Знак абсолютной величины введен в XIX веке Вейерштрассом. Для комплексных чисел это понятие ввели Коши и Арган в XIX веке.
См. также
- Абсолютная величина вещественного числа x есть неотрицательное число, обозначаемое |x| и определяемое следующим образом:
Wikimedia Foundation. 2010.