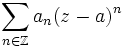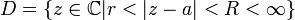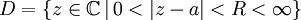- Лорана ряд
-
Ряд Лорана — двусторонне бесконечный степенной ряд по целым степеням (z − a), то есть ряд вида
Этот ряд понимается как сумма двух рядов:
 — правильная часть ряда Лорана и
— правильная часть ряда Лорана и — главная часть ряда Лорана.
— главная часть ряда Лорана.
При этом, ряд Лорана считается сходящимся тогда и только тогда, когда сходятся его правильная и главная части.
Свойства
- Если внутренность области сходимости ряда Лорана непуста, то она представляет собой круговое кольцо
- Во всех точках своего кольца сходимости D ряд Лорана сходится абсолютно;
- Как и для степенных рядов, поведение ряда Лорана в точках граничных окружностей кольца сходимости может быть самым разнообразным;
- На любом компактном подмножестве
 ряд сходится равномерно;
ряд сходится равномерно; - Сумма ряда Лорана в D есть аналитическая функция f(z);
- Ряд Лорана можно дифференцировать и интегрировать в D почленно;
- Разложение в ряд Лорана единственно, то есть если суммы двух рядов Лорана совпадают в D, то совпадают и все коэффициенты этих рядов.
- Коэффициенты an ряда Лорана определяются через его сумму f(z) формулами
-
- где γ(t) = ρet,
![t\in [0,2\pi]](/pictures/wiki/files/49/10e9ceb4f0ea47ca0bfef8df01b9ae3b.png) , r < ρ < R — любая окружность с центром a, расположенная внутри кольца сходимости.
, r < ρ < R — любая окружность с центром a, расположенная внутри кольца сходимости.
Теорема Лорана
Применение ряд Лорана основано главным образом на следующей теореме Лорана:
Любая однозначная аналитическая функция f(z) в кольце
 представима в D сходящимся рядом Лорана.
представима в D сходящимся рядом Лорана.В частности, в проколотой окрестности
изолированной особой точки a однозначная аналитическая функция f(z) представима рядом Лорана, который служит основным инструментом исследования её поведения в окрестности изолированной особой точки.
Тип особой точки определяется главной частью ряда Лорана в кольце с центром в этой точке:
- Устранимая особая точка — главная часть ряда Лорана равна 0.
- Полюс — главная часть содержит конечное число ненулевых членов.
- Существенно особая точка — главная часть содержит бесконечное число ненулевых членов.
Литература
- Шабат Б. В. Введение в комплексный анализ. — М.: Наука. — 1969, 577 стр.
Wikimedia Foundation. 2010.