- ЛОРАНА РЯД
- обобщение степенного ряда по целым неотрицательным степеням разности z-а или по целым неположительным степеням z-а в виде
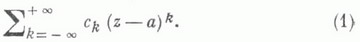
Ряд (1) понимается как сумма двух рядов:
 - правильная часть Л. р. и
- правильная часть Л. р. и
 - главная часть Л. р. Ряд (1) считается сходящимся тогда и только тогда, когда сходятся его правильная и главная части. Свойства Л. р.: 1) если область сходимости Л. р. содержит внутренние точки, то она представляет собой круговое кольцо
- главная часть Л. р. Ряд (1) считается сходящимся тогда и только тогда, когда сходятся его правильная и главная части. Свойства Л. р.: 1) если область сходимости Л. р. содержит внутренние точки, то она представляет собой круговое кольцо 
 с центром в точке
с центром в точке  ; 2) во всех внутренних точках кольца сходимости Dряд (1) сходится абсолютно; 3) как и для степенных рядов, поведение Л. р. в точках граничных окружностей
; 2) во всех внутренних точках кольца сходимости Dряд (1) сходится абсолютно; 3) как и для степенных рядов, поведение Л. р. в точках граничных окружностей  может быть самым разнообразным; 4) на любом компактном множестве
может быть самым разнообразным; 4) на любом компактном множестве  ряд (1) сходится равномерно; 5) сумма ряда (1) в Dесть аналитич. функция f(z); 6) ряд (1) можно дифференцировать и интегрировать в Dпочленно; 7) коэффициенты с k Л. р. определяются через его сумму f(z) формулами
ряд (1) сходится равномерно; 5) сумма ряда (1) в Dесть аналитич. функция f(z); 6) ряд (1) можно дифференцировать и интегрировать в Dпочленно; 7) коэффициенты с k Л. р. определяются через его сумму f(z) формулами

где
 - любая окружность с центром а, расположенная в D;8) разложение в Л. р. единственно, т. е. если
- любая окружность с центром а, расположенная в D;8) разложение в Л. р. единственно, т. е. если  в D, то все коэффициенты их Л. р. по степеням z-асовпадают.
в D, то все коэффициенты их Л. р. по степеням z-асовпадают.
Для случая центра в бесконечно удаленной точке
 Л. р. принимает вид
Л. р. принимает вид

причем теперь правильной частью является
 а главной -
а главной - 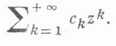
Область сходимости ряда (3) имеет вид

а формулы (2) переходят в формулы

где
 В остальном все свойства те же, что и в случае конечного центра а.
В остальном все свойства те же, что и в случае конечного центра а.
Применение Л. р. основано главным образом на теореме Лорана (1843): любая однозначная аналитич. функция f(z) в кольце

 представима в Dсходящимся Л. р. (1). В частности, в проколотой окрестности
представима в Dсходящимся Л. р. (1). В частности, в проколотой окрестности 
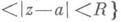 изолированной особой точки а однозначного характера аналитич. функция f(z) представима Л. р., к-рый и служит основным инструментом исследования ее поведения в окрестности изолированной особой точки.
изолированной особой точки а однозначного характера аналитич. функция f(z) представима Л. р., к-рый и служит основным инструментом исследования ее поведения в окрестности изолированной особой точки.
Для голоморфных функций f(z) многих комплексных переменных
 аналогом теоремы Лорана можно считать следующее предложение: всякую функцию f(z), голоморфную в произведении Dколец
аналогом теоремы Лорана можно считать следующее предложение: всякую функцию f(z), голоморфную в произведении Dколец 
 можно представить в Dв виде сходящегося кратного Л. р.
можно представить в Dв виде сходящегося кратного Л. р.

в к-ром суммирование распространяется на все целочисленные мультииндексы

где
 - произведение окружностей
- произведение окружностей 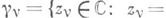

Область сходимости ряда (4) логарифмически выпуклая и является относительно полной кратно круговой областью. Однако применение кратных Л. р. (4) ограничено, поскольку при
 голоморфные функции f(z) не могут иметь изолированных особенностей.
голоморфные функции f(z) не могут иметь изолированных особенностей.
Лит.:[1] Маркушевич А. И., Теория аналитических функций, 2 изд., т. 1, М., 1967, гл. 4; [2] Ш а б а т Б. В., Введение в комплексный анализ, 2 изд., М., 1976, ч. 1, гл. 2, ч. 2, гл. 1. Е. Д. Соломенцев.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
