ВЫЧЕТ

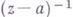аналитической функции f(z) одного комплексного переменного в конечной изолированной особой точке аоднозначного характера - коэффициент при в разложении Лорана функции f(z) (см. Лорана ряд).в окрестности точки а, или равный ему интеграл

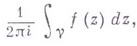
где 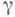- окружность достаточно малого радиуса с центром в точке а. В. обозначается 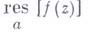(либо Выч. ).

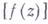Теория вычетов опирается на Коши интегральную теорему. Основной в теории В. является следующая теорема о вычетах. Пусть /(z) - однозначная аналитич. функция всюду в односвяз-ной области G, кроме изолированных особых точек; тогда интеграл от f(z) по любой простой замкнутой спрямляемой кривой g, лежащей в области G и не проходящей через особые точки функции f(z), вычисляется но формуле

где - особые точки функции , попавшие внутрь .

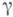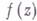Вычет функции в бесконечно удаленной точке для функции , однозначной и аналитической в окрестности этой точки, определяется формулой

где - окружность достаточно большого радиуса, ориентированная по часовой стрелке, а - коэффициент при в разложении Лорана функции 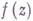в окрестности этой точки.

Из теоремы о В. вытекает теорема о полной сумме вычетов: если f(z)- однозначная аналитич. функция в расширенной комплексной плоскости, кроме конечного числа особых точек, то сумма всех В. функции 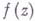, включая В. в бесконечно удаленной точке, равна нулю.

Таким образом, вычисление интегралов от аналитич. функций по замкнутым кривым (контурных интегралов) сводится к вычислению В., к-рые находятся особенно просто в случае конечных полюсов. Пусть - полюс порядка тфункции 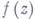, тогда

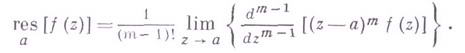
При m=1 (простой полюс) эта формула принимает вид

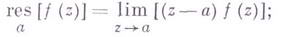
если 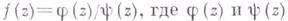регулярны в окрестности точки а, причем для 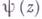точка аесть простой нуль, то

.

Применение теоремы о В. к логарифмич. производной приводит к важной теореме о логарифмическом вычете: если функция 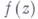мероморфна в односвязной области G, а простая замкнутая кривая лежит в Gи не проходит через нули и полюсы функции , то

где N - число нулей, Р - число полюсов функции внутри с учетом их кратностей. Выражение в левой части этой формулы наз. логарифмическим вычетом функции относительно кривой 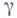(см. также Аргумента принцип).

В. применяются к вычислению нек-рых определенных интегралов от действительных функций, таких, напр., как

где -рациональная функция от непрерывная при - непрерывная функция при где 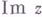- мнимая часть z, и аналитическая при 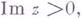кроме конечного числа особых точек. При этом 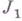подстановкой сводится к контурному интегралу

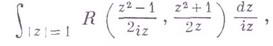
т. е. к вычислению В.;

если

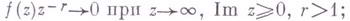
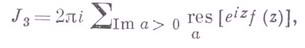
если f (z) удовлетворяет условиям Жордана леммы.

В. находят многочисленные и важные применения в вопросах аналитич. родолжения, разложения мероморфных функций на простейшие дроби, суммирования степенных рядов, асимптотич. оценок и во многих др. вопросах анализа и его приложений (см. |1] - [4]).

Теория В. одного переменного разработана в основном О. Коши (A. Cauchy) в 1825 - 29. Ряд результатов, относящихся к обобщениям теории В. и ее приложениям, был получен Ш. Эрмитом (Ch. Hermite, теорема о сумме В. двоякопериодической функции), П. Лораном (P. Laurent), Ю. В. Сохоцким, Э. Линделёфом и др.

На римановой поверхности рассматриваются В. не аналитич. функций, а аналитических дифференциалов (см. [5]). Вычет аналитического дифференциала в окрестности его изолированной особой точки определяется как коэффициент при в разложении Лорана функции где 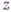- униформизирующий параметр в окрестности этой точки. При этом интеграл от dZ но любой замкнутой кривой на римановой поверхности выражается через В. дифференциала dZ и через его циклические периоды (интегралы от dZ по каноническим разрезам]. На рпмановы поверхности распространяется теорема о полной сумме В.: сумма всех В. мероморфного дифференциала на компактной римановой поверхности равна нулю.

Теория вычетов аналитических функций многих комплексных переменных базируется на интегральных теоремах Стокса и Коши - Пуанкаре, позволяющих заменять интеграл от замкнутой формы по одному циклу интегралом от этой формы по другому циклу, гомологичному первому. Начало теории В. функции многих переменных положил А. Пуанкаре [6], к-рый в 1887 впервые обобщил интегральную теорему Коши и понятие В. на функции двух комплексных переменных, показав, в частности, что интеграл от рациональной функции двух комплексных переменных по двумерному циклу, не проходящему через особенности подинтегральной функции, сводится к периодам абелевых интегралов, и применил двойные В. для обоснования двумерного аналога Лагранжа ряда.

Ж. Лере (J. Leray, см. [7], а также [4], [8]) разработал общую теорию В. на комплексном аналитич. многообразии X. Теория вычетов Лере, в частности, описывает метод вычисления интегралов по нек-рым циклам на Xот замкнутых внешних дифференциальных форм, имеющих особенности на аналитич. одмногообразиях. Вводится понятие вычет-формы, обобщающее понятие В. аналитич. функции одного переменного; получаемая при этом формула В. позволяет свести вычисление интеграла от формы w, имеющей на комплексном аналитич. одмногообразии Sполярную особенность 1-го порядка, по нек-рому циклу в к вычислению интеграла на 1 меньшей размерности от вычет-формы по циклу на S. Для вычисления интегралов от замкнутых форм, имеющих на Sпроизвольные особенности, важны понятие вычет-класса (см. Вычет-форма).и т е-орема Лере, согласно к-рой для любой замкнутой формы найдется когомологичная ей форма шД, имеющая на Sполярную особенность 1-го порядка. Для формы 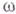, имеющей особенность на нескольких подмногообразиях , используются кратные вычет-форма

вычет-класс

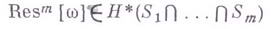
вычет-класс и формула В.

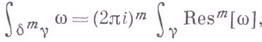
где 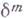- кратный оператор 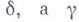- цикл в

Имеется другой подход к теории В. функций многих комплексных переменных - метод выделения базы гомологии, опирающийся на идею Э. Мартинелли (Е. Martinelli) применения Александера двойственности (см. [9]). Пусть f (z), - голоморфная функция в области , а есть n-мерный цикл в G. Если - база n-мерных гомологии области Gи

- разложение апо этой базе, то обобщение теоремы о В. имеет вид

где

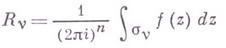
есть n-мерный аналог В. и наз. вычетом функции f (z) относительно базисного циклa s_v. В отличие от случая одной переменной, значительную трудность представляет отыскание как базы гомологии , так и коэффициентов разложения опо базе. В ряде случаев (напр., когда 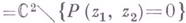, где Р - многочлен) эти задачи позволяет решить двойственность Александера и Понтрягина. При этом коэффициенты находятся как коэффициенты зацепления цикла 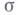с циклами на множестве (компактифицированном определенным образом), двойственными циклам 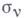. Вычеты 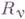в нек-рых случаях находятся как соответствующие коэффициенты разложения Лорана функции .

Многомерные аналоги логарифмич. В. (см. [4], [12]) выражают число общих нулей (с учетом их кратностей) системы голоморфных функций в области через интегралы:

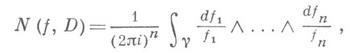
где - нек-рый цикл в В. функций многих переменных нашли применения при изучении фейнмановских интегралов, в комбинаторном анализе (см. [11]) и в теории неявных функций (см. [12]).

Лит.:[1]Маркушевич А. И., Теория аналитических функций, 2 изд., т. 1, М., 1967; [2] Евграфов М. А., Аналитические функции, 2 изд., М., 1968; [3] Привалов И. И., Введение в теорию функций комплексного переменного, 11 изд., М., 1967; [4] Шабат Б. В., Введение в комплексный анализ, М., 1969; [5] Спрингер Д., Введение в теорию римановых поверхностей, пер. с англ., М., 1960; [6] Роinсаre Н., "Acta math.", 1887, t. 9, 321-380; [7] Лере Ж., Дифференциальное и интегральное исчисления на комплексном аналитическом многообразии, пер. с франц., М., 1961; [8] Фукс Б. А., Введение в теорию аналитических функций многих переменных, М., 1962; [9] Южаков А. П., "Изв. ВУЗов. Матем.", 1964, М 5 (42), с. 149-61; [10] Gritfits P. A., "Ann. Math.", 1969, v. 90, № 3,p. 460-95; [11] Егорычев Г. П., Южаков А. П., "Сиб. матем. ж.", 1974, т. 15, № 5, 1049-60; [12] Южаков А. П., Элементы теории многомерных вычетов, Красноярск, 1975. А. П. Южаков.