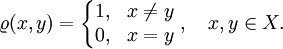- Дискретное множество
-
Дискре́тное простра́нство в общей топологии и смежных областях математики — это пространство, в котором все точки изолированы друг от друга в некотором смысле.
Содержание
Определения
- Пусть X есть некоторое множество, а
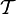 — семейство всех его подмножеств. Тогда
— семейство всех его подмножеств. Тогда 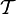 является топологией, называемой дискретной, а пара
является топологией, называемой дискретной, а пара 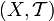 называется дискре́тным топологи́ческим простра́нством.
называется дискре́тным топологи́ческим простра́нством. - Пусть
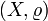 — метрическое пространство, где метрика
— метрическое пространство, где метрика 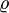 определена следующим образом:
определена следующим образом:
Тогда
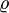 называется дискре́тной ме́трикой, а всё пространство называется дискре́тным метри́ческим простра́нством.
называется дискре́тной ме́трикой, а всё пространство называется дискре́тным метри́ческим простра́нством.Замечание
Топология, индуцированная дискретной метрикой, является дискретной. Обратное, вообще говоря, неверно. Метрика, не являющаяся дискретной, может порождать дискретную топологию.
Примеры
- Пусть
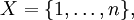 где
где 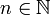 , и
, и 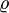 — дискретная метрика на X. Тогда
— дискретная метрика на X. Тогда 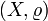 — дискретное метрическое, а следовательно и топологическое пространство.
— дискретное метрическое, а следовательно и топологическое пространство. - Пусть
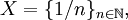 и
и 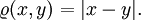 Очевидно, заданная метрика не дискретна. Однако, она порождает дискретную топологию.
Очевидно, заданная метрика не дискретна. Однако, она порождает дискретную топологию.
Свойства
- Топологическое пространство является дискретным тогда и только тогда, когда множество, содержащее лишь одну любую его точку, открыто.
- Множества, содержащие любую одну точку дискретного топологического пространства, являют собой базу дискретной топологии.
- Дискретное топологическое пространство компактно тогда и только тогда, когда оно конечно.
- Дискретное метрическое пространство ограничено.
- Любые два дискретных топологических пространства, имеющих одинаковую мощность, гомеоморфны.
- Любая функция, определённая на дискретном топологическом пространстве, непрерывна.
- Дискретное подмножество евклидова пространства не более чем счётно. Обратное, вообще говоря, неверно.
См. также
- Пусть X есть некоторое множество, а
Wikimedia Foundation. 2010.