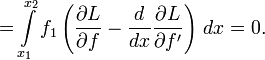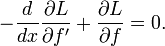- Вариационное исчесление
-
Вариационное исчисление — это раздел математики, в котором изучаются вариации функционалов. Самая типичная задача вариационного исчисления состоит в том, чтобы найти функцию, на которой функционал достигает экстремального значения. Методы вариационного исчисления широко применяются в различных областях математики, в дифференциальной геометрии с их помощью ищут геодезические и минимальные поверхности. В физике вариационный метод — одно из мощнейших орудий получения уравнений движения (см. например Принцип наименьшего действия), как для дискретных, так и для распределённых систем, в том числе и для физических полей. Методы вариационного исчисления применимы и в статике (см. Вариационные принципы).
Важнейшими понятиями вариационного исчисления являются следующие:
- вариация (первая вариация),
- вариационная производная (первая вариационная производная),
- кроме первой вариации и первой вариационной производной, рассматриваются и вариации и вариационные производные второго и высших порядков.
Никак не связана с вариационным вычислением совпадающая по названию вариация функции в анализе.
Термин варьирование (варьировать) — применяется в вариационном исчислении для обозначения нахождения вариации или вариационной производной (это аналог термина дифференцирование для случая бесконечномерного аргумента, являющегося предметом вариационного исчисления). Также нередко для краткости (особенно в приложениях) термин варьирование применяется для обозначения решения вариационной задачи, сводимой к нахождению вариационной производной и приравнивания её нулю.
Вариационная задача означает, как правило, нахождение функции (в рамках вариационного исчисления — уравнения на функцию), удовлетворяющей условию стационарности некоторого заданного функционала, то есть такой функции, (бесконечно малые) возмущения которой не вызывают изменения функционала по крайней мере в первом порядке малости. Также вариационной задачей называют тесно связанную с этим задачу нахождения функции (уравнения на функцию), на которой данный функционал достигает локального экстремума (во многом эта задача сводится к первой, иногда практически полностью). Обычно при таком употреблении терминов подразумевается, что задача решается методами вариационного исчисления.
Типичными примерами вариационной задачи являются изопериметрические задачи в геометрии и механике; в физике — задача нахождения уравнений поля из заданного вида действия для этого поля.
Содержание
История
Одной из первых задач вариационного исчисления известных в истории была задача Дидоны. Другой исторической задачей вариационного исчисления, давшей толчок к развитию этого направления математики является задача о брахистохроне. Решающий вклад в развитие вариационного исчисления внесли Леонард Эйлер и Жозеф Лагранж, первому из которых принадлежит первое систематическое изложение вариационного исчисления и сам термин, второй же получил независимо многие основополагающие результаты и ввёл понятие вариации.
Неформальное обсуждение
Содержанием вариационного исчисления является обобщение понятия дифференциала и производной функции конечномерного векторного аргумента на случай функционала — функции, областью определения которой служит некое множество или пространство функций, а значения лежат в множестве вещественных чисел (иногда комплексных, что мало меняет что-то по существу).
- Всюду ниже в этом параграфе подразумевается, что функции и функционалы обладают необходимой гладкостью, то есть вопрос существования тех или иных производных специально не рассматривается, тем более что во многих конкретных задачах этот вопрос не имеет практического значения (нужная гладкость заведомо есть).
Функционал Φ[f] ставит в соответствие каждой конкретной функции f из его области определения — определённое число.
Нетрудно написать для функционала аналоги дифференциала и производной по направлению.
Вариация
Аналогом дифференциала (первого дифференциала) является в вариационном исчислении вариация (первая вариация):
- δΦ = Φ[f + δf] − Φ[f]
(как и в случае дифференциала имеется в виду линейная часть этого приращения, а выражаясь традиционным образом — δf выбирается бесконечно малой, и при вычислении разности отбрасываются бесконечно малые высших порядков). При этом δf — играющее роль дифференциала или малого приращения независимой переменной — называется вариацией f.
Как видим, δΦ сама в свою очередь является функционалом, так как она, вообще говоря, различна для разных f (также и при разных δf).
Таким образом, это прямой аналог одномерного и конечномерного дифференциала:
- dy = y(x + dx) − y(x)
— точно так же понимаемого как линейная часть приращения функции y при бесконечно малом приращении аргумента x (или линейный член при разложении y по степеням dx вблизи точки x).
Примеры- Для функционала Φ[f] = cos(f(1)) вещественной функции вещественного аргумента — для любой f и δf будет верным δΦ = − sin(f(1)).
- Для функционала Φ[f] = cos(f(1)) + sin(f(6)) вещественной функции вещественного аргумента — для любой f и δf будет верным δΦ = − sin(f(1)) + cos(f(6)).
- Для функционала
![\Phi[f]=\int\limits_1^2 f(x)\,dx](/pictures/wiki/files/51/3606ef9d26024d12e4312e4d97bf4594.png) вещественной функции вещественного аргумента — для любой f и δf будет верным
вещественной функции вещественного аргумента — для любой f и δf будет верным 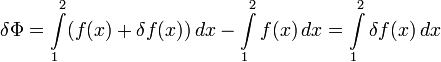 .
.
Производная по направлению
Производной функционала Φ в точке f по направлению g очевидно, будет
Этого в принципе уже достаточно для решения типичной вариационной задачи — нахождения «стационарных точек», то есть таких функций f, для которых первая вариация или производная по направлению обращается в ноль для любой бесконечно малой δf или любой конечной g. Именно эти «точки» в пространстве функций — то есть именно такие функции — являются кандидатами в экстремали (проверку того, действительно ли они являются экстремалями, то есть достигается ли на них локальный экстремум, надо делать отдельно, как и в случае функций конечномерного аргумента; интересно, что во многих задачах физики важнее найти не экстремали, а именно стационарные точки).
Примеры- (Здесь не вводится специальных обозначений для производной по направлению.)
- Производная функционала Φ[f] = f(0) в точке f = cos по направлению g = cos равна
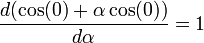 .
. - Производная функционала Φ[f] = f(0) в точке f = cos по направлению g = sin равна
 .
. - Производная функционала
![\Phi[f]=\int\limits_0^{2\pi}\cos(x)f(x)\,dx](/pictures/wiki/files/98/b631c555344d6ddc9e6f100dc0b257a2.png) в точке f = cos по направлению g = cos равна
в точке f = cos по направлению g = cos равна 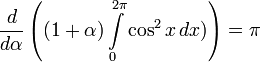 .
. - Производная функционала
![\Phi[f]=\int\limits_0^{2\pi}\cos(x)f(x)\,dx](/pictures/wiki/files/98/b631c555344d6ddc9e6f100dc0b257a2.png) в точке f = cos по направлению g = sin равна
в точке f = cos по направлению g = sin равна 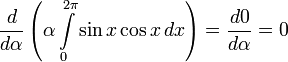 .
.
Вариационная производная
Для интегральных функционалов, которые являются очень важным для математики и приложений случаем, можно ввести не только аналог дифференциала и производную по направлению, но и производную Фреше — аналог конечномерного (градиента), называемую вариационной производной.
То есть, в полной аналогии с конечномерным случаем, когда
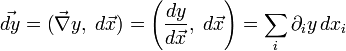 ,
,
где
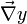 — обозначение градиента (или производной Фреше) функции y, а
— обозначение градиента (или производной Фреше) функции y, а  — скалярное произведение;
— скалярное произведение; 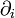 — оператор частной производной по i-той координате, сумма представляет собой полный дифференциал.
— оператор частной производной по i-той координате, сумма представляет собой полный дифференциал.Для функционала имеем
 ,
,
где
 — обозначение вариационной производной Φ, а суммирование конечномерной формулы естественно заменено интегрированием.
— обозначение вариационной производной Φ, а суммирование конечномерной формулы естественно заменено интегрированием.Итак,
 — стандартное обозначение вариационной производной. Это также некая функция как от x, как и f (вообще говоря, это обобщённая функция, но эта оговорка выходит за рамки рассмотрения, так как предполагается, что все функции и функционалы сколь угодно гладки и не имеют особенностей).
— стандартное обозначение вариационной производной. Это также некая функция как от x, как и f (вообще говоря, это обобщённая функция, но эта оговорка выходит за рамки рассмотрения, так как предполагается, что все функции и функционалы сколь угодно гладки и не имеют особенностей).
Иными словами, если можно представить вариацию
- δΦ = Φ[f + δf] − Φ[f]
в виде
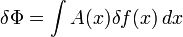 , где A — некоторая функция x,
, где A — некоторая функция x,
то A есть вариационная производная Φ по f («по f» здесь означает, что остальные аргументы или параметры не меняются; речевой оборот «по f» можно опустить в случае, когда точно определено, функционалом от какой функции рассматривается Φ, что на практике может быть не ясным из самой его формулы, в которую могут входить и другие параметры и функции — см. также ниже). То есть
Примеры- (В здесь разность интегралов сводится в один интеграл.)
- Для функционала
![\Phi[f]=\int\limits_1^2 f(x)\,dx](/pictures/wiki/files/51/3606ef9d26024d12e4312e4d97bf4594.png) имеем
имеем
- Для функционала
![\Phi[f]=\int\limits_1^2 K(x)f(x)\,dx](/pictures/wiki/files/53/5f3ddef333d6b3689b8d19ba65b2da45.png) вариационная производная вычисляется как:
вариационная производная вычисляется как:
- Для функционала
![\Phi[f]=\int\limits_1^2 L(f(x))\,dx](/pictures/wiki/files/100/dfc74a5db6a54cba876e3a75932acb2c.png)
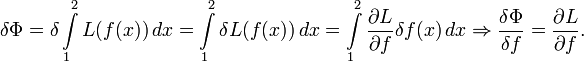
- Если выразить бесконечно малую разность функции δL(f) через её производную и разность аргумента δf, получается:

Легко видеть, что это определение обобщается на любую размерность интеграла. Для n-мерного случая верна прямо обобщающая одномерный случай формула:
Так же легко обобщается понятие вариационной производной на случай функционалов от нескольких аргументов[1]:
Примеры- (В здесь разность интегралов сводится в один интеграл.)
- Для функционала
![\Phi[f]=\int\limits_1^2\int\limits_3^4 L(f(x,\;y))\,dx\,dy](/pictures/wiki/files/50/203e69bb299a43dd366add88b7634e16.png) многомерный случай вариационной производной вычисляется как:
многомерный случай вариационной производной вычисляется как:
- Для функционала
![\Phi[f,\;g]=\int\limits_1^2 L(f(x),\;g(x))dx](/pictures/wiki/files/49/1c60227745a39d96ad93f10ce8102a89.png) имеем
имеем
Выражая бесконечно малую разность функции нескольких аргументов как полный дифференциал, получим:
Вариации и вариационные производные второго и высших порядков
Как это описано выше для первого порядка, можно ввести понятие второй вариации и второй вариационной производной функционала, а также n-ой вариации и n-ой вариационной производной:
Для функционалов, зависящих от нескольких функций, можно также ввести понятие смешанных вариационных производных разного порядка, например:
Здесь мы не будем останавливаться на этом подробно, всё делается полностью аналогично введению соответствующих дифференциалов и производных для функции конечномерного аргумента.Функционал вблизи конкретной точки в пространстве функций раскладывается в ряд Тейлора, если, конечно, вариационные производные всех порядков существуют. Как и в конечномерных случаях, сумма конечного числа членов этого ряда даёт значение функционала с определённой точностью (соответствующего порядка малости) лишь при небольших отклонениях его аргумента (при бесконечно малых). Кроме того, как и в случае функций конечномерного аргумента, ряд Тейлора (сумма всех членов) может не сходиться к функционалу, в него разложенному, при любых ненулевых конечных смещениях, хотя такие случаи достаточно редки в приложениях.
Применение вариационного исчисления
Хотя задачи, к которым применимо вариационное исчисление, заметно шире, в приложениях они главным образом сводятся к двум основным задачам:
- нахождение точек в пространстве функций, на котором определён функционал — точек стационарного функционала, стационарных функций, линий, траекторий, поверхностей и т. п., то есть нахождение для заданного Φ[f] таких f, для которых δΦ = 0 при любом (бесконечно малом) δf, или, иначе, где
 ,
, - нахождение локальных экстремумов функционала, то есть в первую очередь определение тех f, на которых Φ[f] принимает локально экстремальные значения — нахождение экстремалей (иногда также определение знака экстремума).
Очевидно, обе задачи тесно связаны, и решение второй сводится (при должной гладкости функционала) к решению первой, а затем проверке, действительно ли достигается локальный экстремум (что делается независимо вручную, или — более систематически — исследованием вариационных производных второго и, если все они одного знака и хотя бы одна из них равна нулю, то производных более высокого порядка). В описанном процессе выясняется и тип экстремума. Нередко (например, когда функция стационарного функционала единственная, а все изменения функционала при любом большом возмущении имеют один и тот же знак) решение вопроса, экстремум ли это и какого он типа, заранее очевидно.
При этом очень часто задача (1) оказывается не менее или даже более важной, чем задача (2), даже когда классификация стационарной точки неопределённа (то есть она может оказаться минимумом, максимумом или седловой точкой, а также слабым экстремумом, точкой, вблизи которой функционал точно постоянен или отличается от постоянного в более высоком порядке, чем второй). Например, в механике (и вообще в физике) кривая или поверхность стационарной потенциальной энергии означает равновесие, а вопрос, является ли она экстремалью, связан лишь с вопросом об устойчивости этого равновесия (который далеко не всегда важен). Траектории стационарного действия отвечают возможному движению, независимо от того, минимально действие на такой траектории, максимально, или седловидно. То же можно сказать о геометрической оптике, где любая линия стационарного вермени (а не только минимального, как в простой формулировке принципа наименьшего времени Ферма) соответствует возможному движению светового луча неоднородной оптической среде. Есть системы, где вообще нет экстремалей, но стационарные точки существуют.
Способы нахождения условных экстремумов и условных стационарных точек (см. ниже) делают вариационное исчисление ещё более мощным орудием решения обеих задач.
Техника варьирования
Основным техническим вопросом при нахождении вариационной производной интегрального функционала Φ[f], в подынтегральное выражение которого входит не только значение функции f в точке x, но и значения ее производных, то есть не только f(x), но и df / dx, d2f / dx2 и так далее (в принципе могут входить производные любого порядка, хотя в практических задачах порядки, выше второго, встречаются гораздо реже). Производные входят туда практически всегда: например, такой функционал, как длина кривой, содержит производные первого порядка, а потенциальная энергия изогнутого упругого стержня — производные по меньшей мере второго порядка.
Неудобство[2], заключающееся в том, что при этом в выражении δΦ[f] появляются под интегралом не только члены с δf, но и с δ(df / df), устраняется интегрированием по частям.
Рассмотрим это сначала на простом частном примере, а затем на общем.
Пример: Пусть требуется найти вариационную производную функционала
![\Phi[f]=\int\limits_1^2\left((f'(x))^2+(f(x))^3\right)\,dx](/pictures/wiki/files/49/1caa911275a48bf85ca6ad240d660f50.png) , где штрихом обозначена производная по x, и f(x), для которых значение Φ экстремально.
, где штрихом обозначена производная по x, и f(x), для которых значение Φ экстремально.Нетрудно выписать
Очевидно, операцию взятия производной по x свободно можно поменять местами с операцией δ. Тогда
Теперь, чтобы δf(x) не стояло под знаком производной, мешающего вынести за скобки δf(x) из обоих членов (оставшееся в скобках суть вариационная производная), надо в первом слагаемом воспользоваться интегрированием по частям:
Теперь можно опять превратить сумму интегралов в один и вынести за скобки δf:
оставив граничный член
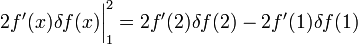 , стоящим отдельно.
, стоящим отдельно.Граничный член можно приравнять нулю[3], решив тем самым задачу нахождения вариационной производной (действительно, она по определению есть то, что стоит под интегралом в больших скобках, соответствовать определению мешает только граничный член). Объяснение факта равенства нулю граничного члена не слишком строго (см. примечание [3]), но ограничимся им, чтобы сосредоточить внимание на главном.
Для начала зафиксируем f в граничных точках, тогда граничный член исчезнет, так как δf должно будет при такой фиксации обращаться в ноль при x = 1 и x = 2. Для многих задач такая фиксация граничных условий имеет место изначально. При поиске экстремума и вариационной производной на классе функций с такими граничными условиями граничный член можно просто отбросить. Но если граничные условия не наложены самой задачей, их можно наложить искусственно, решить задачу для фиксированных условий, а затем среди множества решений для разных граничных условий можно выбрать оптимальное (это обычно не составляет труда). Короче говоря, решение задачи с обнулением граничного члена содержит в себе среди прочих и решение первоначальной задачи, нужно лишь сузить класс уже найденных решений, меняя f(1) и f(2) и подобрав среди них лучшее. (Более аккуратный и общий подход — см. ниже).
Таким образом, здесь под вариационной производной будем понимать вариационную производную по классу функций с фиксированными концами, которая (при поиске экстремали и в подобных задачах) будучи приравненной нулю, определяет поведение функции внутри отрезка
![[1;\;2]](/pictures/wiki/files/101/e56884b45a583fa44e43b747ca791487.png) . В этом смысле, для нашего примера имеем:
. В этом смысле, для нашего примера имеем:а необходимое условие экстремальности состоит в равенстве её нулю, то есть имеем уравнение для f:
Решение этого дифференциального уравнения даст явный вид f(x), но задача нахождения решений дифференциального уравнения лежит уже за рамками вариационного исчисления. Задача последнего ограничена получением такого уравнения и, возможно, дополнительных условий, ограничивающих класс допустимых решений.
Использование обобщённых функций
В этом разделе рассмотривается такой частный, но практически важный, случай применения обобщённых функций при решении вариационных задач, как использование дельта-функции Дирака.
Использование δ-функции (не следует путать ее обозначение δ(x) с символом вариации!), как и использование обобщённых функций вообще, позволяет значительно расширить класс функционалов, которые могут быть записаны в форме интегральных функционалов, и к которым, следовательно, применимы основные приёмы вариационного исчисления (описанные выше). При этом в число функционалов, записываемых в такой форме, попадают такие практически важные функционалы, как краевые функционалы, что сильно облегчает работу с ними и делает её систематичной.
- Для облегчения восприятия данного раздела, будем выделять дельта-функцию жирным шрифтом:
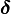 — чтобы отличать от символа вариации.
— чтобы отличать от символа вариации.
Рассмотрим простой пример. Пусть надо найти функцию f(x), минимизирующую функционал
![W[f]=\frac{1}{2}\int\limits_0^1(f'(x))^2\,dx](/pictures/wiki/files/50/29a2f062be8970c00c5d3df3f45a73b6.png) притом, что на неё наложены условия
притом, что на неё наложены условия  .
.Для того, чтобы было удобно решать эту задачу, наложенные условия полезно записать в виде
![\Gamma_0[f]=10,\;\Gamma_1[f]=20](/pictures/wiki/files/54/6a2185e6c16b16f8c2d0f12f0566fd43.png) (в этом случае,
(в этом случае, ![\Gamma_0[f]=f(0),\;\Gamma_1[f]=f(1)](/pictures/wiki/files/100/d8c31eddb3d39f38319a0c269982a421.png) суть функционалы). Не ограничиваясь этим, используя основное свойство дельта-функции, запишем Γ0 и Γ1 в интегральной форме:
суть функционалы). Не ограничиваясь этим, используя основное свойство дельта-функции, запишем Γ0 и Γ1 в интегральной форме:Теперь можно (расширив область интегрирования в определении W, хотя бы на бесконечно малую величину, за пределы отрезка [0;1]) свободно складывать и вычитать[4] функционалы
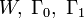 , что позволяет формально просто свести решение исходной задачи к задаче об условном экстремуме функционала (см. ниже), сводящейся к отысканию экстремума нового функционала V = W − λ0Γ0 − λ1Γ1 с постоянными множиталями
, что позволяет формально просто свести решение исходной задачи к задаче об условном экстремуме функционала (см. ниже), сводящейся к отысканию экстремума нового функционала V = W − λ0Γ0 − λ1Γ1 с постоянными множиталями 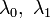 , конкретные значения которых после решения задачи по отысканию минимума V нужно подобрать, решив соответствующие алгебраические уравнения. Таким образом, граничные условия будут удовлетворены. А главное, функционал V при этом будет иметь вполне прозрачную интегральную форму, удобную для варьирования.
, конкретные значения которых после решения задачи по отысканию минимума V нужно подобрать, решив соответствующие алгебраические уравнения. Таким образом, граничные условия будут удовлетворены. А главное, функционал V при этом будет иметь вполне прозрачную интегральную форму, удобную для варьирования.Сходный приём удобен при наложении на искомую фунцию не граничных условий, а условий удовлетворения некоторому уравнению в каждой точке x.
Условные экстремумы
- Для краткости будем говорить в этом разделе об условных экстремумах, однако всё здесь написанное ра́вно приложимо к нахождению стационарных точек вообще.
Условным экстремумом называется экстремум не на всей области определения функции (функционала), а на определённом её подмножестве, выделяемом специально наложенным условием (или условиями). Обычно, речь идёт о выделении этим условием (условиями) подмножества области определения с меньшей размерностью, что для конечномерных областей имеет определённый наглядный смысл, но для бесконечномерных (каковы обычно области определения функционалов) налагаемые условия приходится рассматривать лишь абстрактно (что теоретически не мешает иметь в виду полезную аналогию с конечномерным случаем).
Пусть надо найти экстремум функционала Φ[f] при некотором наложенном условии.
Замечания и примерыКак обычно, тривиальный случай, когда наложенное условие сводится к явному выражению чего-то через что-то (например, если известно, что
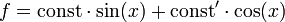 ), нет смысла специально рассматривать, так как это приводит просто к некоторому переписыванию функционала в новом виде (или даже к сведению функционала к функции конечного количества переменных).
), нет смысла специально рассматривать, так как это приводит просто к некоторому переписыванию функционала в новом виде (или даже к сведению функционала к функции конечного количества переменных).Рассмотрения заслуживает случай, когда налагаемое в виде равенства нулю (в общем случае, константе) неких других функционалов (одного или нескольких), или наложение на искомую функцию уравнения, которому она должна удовлетворять.
Типичный случай первой задачи с одним наложенным условием — изопериметрическая задача (например, задача Дидонны). Примером второго типа условия может быть наложение в некоторых физических задачах требования подчинению уравнению непрерывности (для стационарных задач — его стационарного варианта
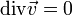 ).
).Основные виды задачи на условный экстремум, которые имеет смысл рассмотреть, таковы:
- Надо найти экстремум функционала
![U[f]\](/pictures/wiki/files/55/7f2d25c120f3093538234aeb4c4d4a87.png) при условии равенства нулю другого функционала
при условии равенства нулю другого функционала ![V[f]=0\](/pictures/wiki/files/48/04fe9304ad3ded23de0e9970cac86535.png) ; (то, что в правой части нуль, не нарушает общности).
; (то, что в правой части нуль, не нарушает общности). - Надо найти экстремум функционала
![U[f]\](/pictures/wiki/files/55/7f2d25c120f3093538234aeb4c4d4a87.png) при условии
при условии ![V_1[f]=0,\;V_2[f]=0,\;\ldots,\;V_N[f]=0](/pictures/wiki/files/53/5f52250d815adf29a44189ff94dc63c1.png) .
. - Надо найти экстремум функционала
![U[f]\](/pictures/wiki/files/55/7f2d25c120f3093538234aeb4c4d4a87.png) при условии выполнения для
при условии выполнения для 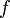 уравнения
уравнения 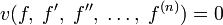 , где
, где 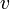 — некоторая функция
— некоторая функция 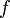 и/или производных
и/или производных 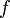 , обозначенных штрихами.
, обозначенных штрихами.
(Третий тип условия выписан здесь не в самом общем виде, но для наших целей этого достаточно.)
К первым двум случаям практически прямо (на принятом сейчас нами уровне строгости нет смысла проводить тут границу между случаем функций конечномерного аргумента, и функционалами) применим метод неопределенных множителей Лагранжа. А именно, для нахождения условного экстремума
![U[f]\](/pictures/wiki/files/55/7f2d25c120f3093538234aeb4c4d4a87.png) при наложении соответстсующих условий, нужно решить вариационную задачу для функционала
при наложении соответстсующих условий, нужно решить вариационную задачу для функционала ![\hat U[f] = U[f] - \lambda V[f]](/pictures/wiki/files/52/46aab4971ba935eae9f04ec81fdbec6c.png) в первом и
в первом и ![\hat U[f] = U[f] - \lambda_1 V_1[f] - \lambda_2 V_2[f]- \dots - \lambda_N V_N[f]](/pictures/wiki/files/55/7d5b574a3f817fb636a88db378453d81.png) во втором случае, а затем подобрать (решив уравнение
во втором случае, а затем подобрать (решив уравнение 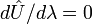 в первом случае и N уравнений с частными производными по каждому из λi во втором) такие λ, которые реализуют минимум в найденном семействе функций f, для котого эти λ являются параметрами. То есть, что касается вариационного исчисления, то ключевым моментом является нахождение и приравнивание нулю вариации (или вариационной производной) для некоего нового функционала
в первом случае и N уравнений с частными производными по каждому из λi во втором) такие λ, которые реализуют минимум в найденном семействе функций f, для котого эти λ являются параметрами. То есть, что касается вариационного исчисления, то ключевым моментом является нахождение и приравнивание нулю вариации (или вариационной производной) для некоего нового функционала ![\hat U[f]](/pictures/wiki/files/56/8d0d12369542933fca6dc4b8d7e1012d.png) , для этих двух случаев:
, для этих двух случаев:Третий же случай рассмотрим здесь для интегрального функционала
![U[f] = \int\limits_\Omega \dots d\Omega](/pictures/wiki/files/99/c2c7ea8f78f06dace93df79709eea51f.png) . Тогда нахождение условного экстремума сводится сначала к варьированию функционала
. Тогда нахождение условного экстремума сводится сначала к варьированию функционала![\hat U[f] = U[f] - \int\limits_\Omega \lambda(x) v(f,\;f',\;f'',\;\ldots,\;f^{(n)})d\Omega](/pictures/wiki/files/97/a86d5ef3c734bab3b46b8cbafbf9d524.png)
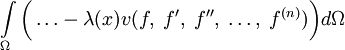 ,
,
где x - переменная, принадлежащая области интегрирования Ω (одномерной или n-мерной), а λ(x) - некая неопределенная функция x, которая войдет в уравнение, полученное после вычисления вариационной производной и приравнивания ее нулю.
Обоснованием такого решения для случая 3 может служить представление для каждой точки x0 из Ω выполнения равенства
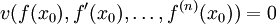 в x0 как приравнивание нулю функционала
в x0 как приравнивание нулю функционала  с использованием дельта-функции Дирака. Далее можно считать на рассматриваемом здесь неформальном уровне очевидным, что задача стала аналогичной варианту 2, и, после суммирования по всем x0, ее решение сводится к описанному выше.
с использованием дельта-функции Дирака. Далее можно считать на рассматриваемом здесь неформальном уровне очевидным, что задача стала аналогичной варианту 2, и, после суммирования по всем x0, ее решение сводится к описанному выше.Таким образом, ключевой момент с точки зрения вариационного исчисления в нахождении условного экстремума третьего типа сводится к
- 3.

- Под производными при многомерном x можно иметь в виду, например, частные производные разного порядка, в том числе смешанные.
Уравнение Эйлера — Лагранжа
Одним из основных классических результатов вариационного исчисления, имеющих огромное практическое значение, являются уравнения Эйлера — Лагранжа — дифференциальные уравнения, которым должна удовлетворять функция, являющаяся стационарной для довольно общего в своем классе и очень важного вида интегрального функционала (а значит и функция, на которой такой функционал достигает локального экстремума, тоже должна необходимо удовлетворять этим уравнениям).
Здесь приводится вывод уравнений Эйлера — Лагранжа с использованием производной функционала по направлению.
Вывод с использованием производной по направлению. Частный пример
Для гладких функций вещественной переменной или конечномерного векторного аргумента максимум и минимум заданной функции может быть найден путём нахождения точек, в которых производная обращается в нуль (по крайней мере, это необходимое условие экстремума). Аналогично решение гладких задач вариационного исчисления может быть получено путём решения соответствущего уравнения Эйлера — Лагранжа.
Чтобы проиллюстрировать этот процесс, рассмотрим сначала конкретную задачу нахождения кратчайшей кривой на плоскости, соединяющей две точки
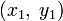 и
и 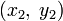 . Длина кривой определяется выражением
. Длина кривой определяется выражениемгде
и где y = f(x), f(x1) = y1 и f(x2) = y2. Функция f должна иметь хотя бы одну производную. Если f0 — локальный минимум и f1 — подходящая функция, обращающаяся в нуль в граничных точках x1 и x2 и имеющая хотя бы первую производную, тогда мы получим
для любого
 , близкого к 0. Следовательно, производная
, близкого к 0. Следовательно, производная ![A[f_0+\varepsilon f_1]](/pictures/wiki/files/56/8951e653c7ace5108fcf68569b3e085e.png) по
по  (первая вариация A) должна обращаться в нуль при
(первая вариация A) должна обращаться в нуль при 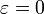 . Таким образом,
. Таким образом,при любом выборе функции f1. Если предположить, что f0 имеет вторую непрерывную производную, тогда можно воспользоваться формулой интегрирования по частям:
После замены
получается
но первое слагаемое обращается в нуль, поскольку v(x) = f1(x) было выбрано таким образом, чтобы обращаться в нуль в точках x1 и x2. Следовательно,
для любой дважды дифференцируемой функции f1, которая обращается в нуль на концах интервала. Это особый случай основной леммы вариационного исчисления:
для любой дифференцируемой функции f1(x), которая обращается в нуль на концах интервала. Поскольку f1(x) есть произвольная функция в интервале интегрирования, можно сделать вывод, что H(x) = 0. Тогда,
Из этого уравнения следует, что
Таким образом, экстремумом в нашей задаче являются отрезки прямых линий.
Вывод с использованием производной по направлению. Более общий случай
Подобные же вычисления можно провести и в общем случае[5], когда
и f должна иметь две непрерывные производные. Повторяя рассуждения, находим экстремаль f0, принимаем
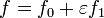 , находим производную по
, находим производную по  , затем подставляем
, затем подставляем 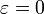 :
:Наконец, в силу основной леммы вариационного исчисления можно заключить, что функция L должна удовлетворять уравнению Эйлера — Лагранжа
В общем случае, это уравнение является обыкновенным дифференциальным уравнением второго порядка, решив которое, можно найти экстремаль f.
Уравнение Эйлера — Лагранжа является необходимым, но не достаточным условием наличия экстремума. Дополнительные условия формулируются отдельно.
Примечания
- ↑ Формально можно свести функционал нескольких аргументов
![\Phi_n[f_1,\;f_2,\;\ldots,\;f_n]](/pictures/wiki/files/102/fb94756a45a4bdde72ccb5b4d42cdc0c.png) , использовав функцию с множеством значений, в более многомерном пространстве
, использовав функцию с множеством значений, в более многомерном пространстве 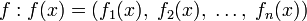 , к функционалу, зависящему от одной этой новой функции Φ1[f], но чисто технически нередко бывает удобнее использовать первоначальный вариант без изменений, так как при конкретных вычислениях всё сводится в конечном счёте к покомпонентному расчёту, когда все
, к функционалу, зависящему от одной этой новой функции Φ1[f], но чисто технически нередко бывает удобнее использовать первоначальный вариант без изменений, так как при конкретных вычислениях всё сводится в конечном счёте к покомпонентному расчёту, когда все  — вещественнозначные (в крайнем случае, комплекснозначные) функции.
— вещественнозначные (в крайнем случае, комплекснозначные) функции. - ↑ Неудобство тут прежде всего в том, что производные мешают вынести все δf за скобки, приведя δΦ к виду
 , что и означает нахождение вариационной производной (которая есть всё, что стоит в скобках и обозначено многоточием). Но даже если функционал таков, что производная легко выносится за скобки, то есть вариацию можно представить в виде
, что и означает нахождение вариационной производной (которая есть всё, что стоит в скобках и обозначено многоточием). Но даже если функционал таков, что производная легко выносится за скобки, то есть вариацию можно представить в виде 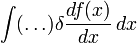 , то от дифференцирования δf всё равно необходимо избавиться. Это необходимо, исходя из тех соображений, что по определению (и по смыслу) при вариационной производной под интегралом должно стоять только δf, и что df / dx оказывается уже не «любой» функцией x. В противном случае, при поиске экстремума, может найтись неучтённое направление, по которому
, то от дифференцирования δf всё равно необходимо избавиться. Это необходимо, исходя из тех соображений, что по определению (и по смыслу) при вариационной производной под интегралом должно стоять только δf, и что df / dx оказывается уже не «любой» функцией x. В противном случае, при поиске экстремума, может найтись неучтённое направление, по которому 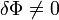 . То, что df / dx — уже не любая функция, легко увидеть при наложении граничных условий. Как описано в статье, это затруднение легко разрешаемо.
. То, что df / dx — уже не любая функция, легко увидеть при наложении граничных условий. Как описано в статье, это затруднение легко разрешаемо. - ↑ 1 2 Используя дельта-функцию Дирака, можно получить более строий результат сразу с учётом граничного члена, но здесь, для упрощения изложения, обойдёмся таким подходом.
- ↑ Конечно, операция сложения и вычитания функционалов в принципе определена независимо от формы их записи, однако использование одинаковой формы сводит ее к совершенно автоматической, прозрачной и технически удобной, так как всё теперь сводится просто к сложению интегралов по одной и той же области, а значит — к сложению подынтегральных выражений.
- ↑ Здесь явно разобран случай, где функция Лагранжа L имеет аргументами всего одну функцию f и одну её первую производную (этот случай наиболее важен практически), причём интегрирование ведётся по одной вещественной переменной. Однако теорема и доказательство достаточно легко и прямо обобщаются на любое конечное число аргументов, любой конечный порядок по производным, и на формулировку с интегрированием по конечномерной области.
Литература
- Краснов М. Л., Макаренко Г. И., Кисилев А. И. Вариационное исчисление, задачи и упражнения. — М.: Наука, 1973
- Эльсгольц Л. Э. Дифференциальные уравнения и вариационное исчисление. — М.: Наука, 1969
- Алексеев В. М., Тихомиров В. М., Фомин С. В. Оптимальное управление. — М.: Наука, 1979
- Дубровин Б. А., Новиков С. П., Фоменко А. Т. Современная геометрия: Методы и приложения. — М.: Наука, 1979
- Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. Том 6: Электродинамика. Перевод с английского (издание 3). — Эдиториал УРСС. — ISBN 5-354-00704-6 — глава 19: Принцип наименьшего действия. (Очень простое, неформальное и наглядное введение в технику варьирования на примере принципа наименьшего действия; рекомендуется для старших школьников и, быть может, студентов младших курсов).
См. также
Wikimedia Foundation. 2010.

![\frac{d\Phi[f+\alpha g]}{d\alpha}\bigg|_{\alpha=0}.](/pictures/wiki/files/54/62f1ee6293a7e130db65174396175c28.png)
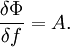

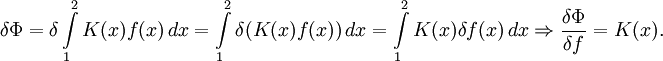

![\delta\Phi[f,\;g,\;\ldots]=\int\limits_\Omega\left(\frac{\delta\Phi}{\delta f}\delta f(x)+\frac{\delta\Phi}{\delta g}\delta g(x)+\ldots\right)\,d\Omega.](/pictures/wiki/files/97/ad996786a0448d12c2de21cc11aadb1e.png)
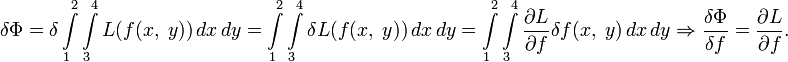
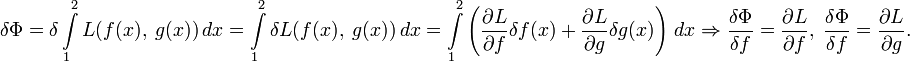
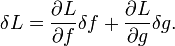
![\delta^2\Phi,\;\frac{\delta^2\Phi[f]}{\delta f^2},\;\delta^n\Phi,\;\frac{\delta^n\Phi[f]}{\delta f^n}.](/pictures/wiki/files/97/a085314abdec91df78409e3f6116c15c.png)
![\frac{\delta^3\Phi[f,\;g]}{\delta f^2\delta g}.](/pictures/wiki/files/55/781e2925e455d190d68d576c57670c5d.png)
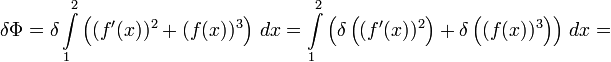
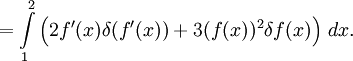

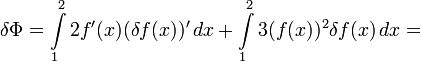

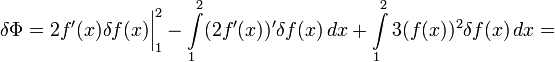
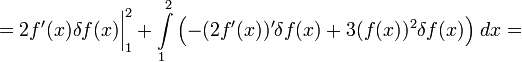
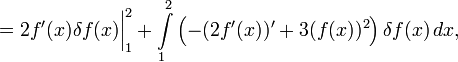
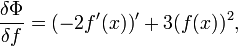
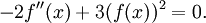
![\Gamma_0[f]=\int\limits_{-\infty}^{+\infty}\boldsymbol\delta(x-0)f(x)\,dx,](/pictures/wiki/files/101/e4fbff578e56d9163bdea6509745ab0f.png)
![\Gamma_1[f]=\int\limits_{-\infty}^{+\infty}\boldsymbol\delta(x-1)f(x)\,dx.](/pictures/wiki/files/100/d596858ea3b6aee646fa94942856e32e.png)

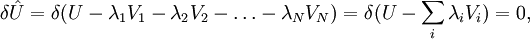
![A[f]=\int\limits_{x_1}^{x_2}\sqrt{1+[f'(x)]^2}\,dx,](/pictures/wiki/files/97/a1803ab91b28a0ad2bb9cff66d69ce1b.png)

![A[f_0]\leqslant A[f_0+\varepsilon f_1]](/pictures/wiki/files/50/233de0303f153f4939455646b43fb79f.png)
![\int\limits_{x_1}^{x_2}\frac{f_0'(x)f_1'(x)}{\sqrt{1+[f_0'(x)]^2}}\,dx=0](/pictures/wiki/files/97/ab657a9bd58806fd5226b0e9f6fbbe21.png)
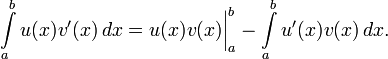
![u(x)=\frac{f_0'(x)}{\sqrt{1+[f_0'(x)]^2}},\quad v'(x)=f_1'(x),](/pictures/wiki/files/57/942eb6c4159a48e29a37cc838cdc3391.png)
![u(x)v(x)\bigg|_{x_1}^{x_2}-\int\limits_{x_1}^{x_2} f_1(x)\frac{d}{dx}\left[\frac{f_0'(x)}{\sqrt{1+[f_0'(x)]^2}}\right]\,dx=0,](/pictures/wiki/files/54/6bba2f726aaf73a79e1bd832358e4375.png)
![\int\limits_{x_1}^{x_2} f_1(x)\frac{d}{dx}\left[\frac{f_0'(x)}{\sqrt{1+[f_0'(x)]^2}}\right]\,dx=0](/pictures/wiki/files/51/3172f5a20cf2b2a3e561a1d8373d12c5.png)

![\frac{d}{dx}\left[\frac{f_0'(x)}{\sqrt{1+[f_0'(x)]^2}}\right]=0.](/pictures/wiki/files/55/789180afa1e67729437cfe6cb1007739.png)
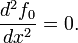
![A[f]=\int\limits_{x_1}^{x_2} L(x,\;f,\;f')\,dx](/pictures/wiki/files/101/e7115444839a6acba80acbad486f1a1e.png)