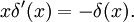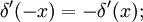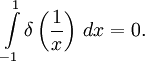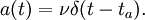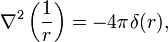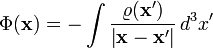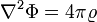- Дельта-функция Дирака
-
δ-функция (или дельта-функция, δ-функция Дирака, дираковская дельта, Единичная импульсная функция) позволяет записать пространственную плотность физической величины (масса, заряд, интенсивность источника тепла, сила и т. п.), сосредоточенной или приложенной в одной точке.
Например, плотность точечной массы 1, находящейся в точке a евклидова пространства
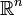 , записывается с помощью δ-функции в виде δ(x − a). Также применима для описания распределений заряда, массы и т. п. на поверхностях или линиях.
, записывается с помощью δ-функции в виде δ(x − a). Также применима для описания распределений заряда, массы и т. п. на поверхностях или линиях.δ-функция есть обобщённая функция, это означает, что формально она определяется как непрерывный линейный функционал на пространстве дифференцируемых функций.
δ-функция не является функцией в классическом смысле, тем не менее нетрудно указать последовательности обычных классических функций, слабо сходящуюся к δ-функции.
Введена английским физиком Дираком.
Можно различать одномерную и многомерные дельта-функции, однако последние могут быть представлены в виде произведения одномерных в количестве, равном размерности пространства, на котором определена многомерная.
Определение
δ-функция с областью определения
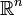 определяется формальным соотношением
определяется формальным соотношениемдля любой непрерывной функции
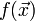 .
.В частности, для одномерной дельта-функции (то есть дельта-функции с областью определения
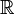 )
)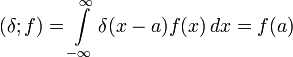 .
.
Альтернативное определение
Для дельта-функции одной вещественной переменной верны следующие равенства:
 ;
;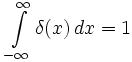 .
.
-
- аналогичные свойства верны и для дельта-функций, определённых на

- аналогичные свойства верны и для дельта-функций, определённых на
Формально эти равенства не являются определением дельта-функции, однако во многих учебниках по физике она определяется именно так, и этого достаточно для решения физических задач.
Свойства
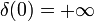
- Интеграл от дельта-функции по любому интервалу, содержащему в себе ноль, то есть интервалу вида ( − a1,a2), где a1 и a2 — произвольные действительные положительные числа, равен 1.
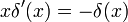
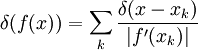 , где xk — нули функции f(x).
, где xk — нули функции f(x).
- Первообразной одномерной дельта-функции является функция Хевисайда:
δ-функция как слабый предел
Пусть
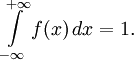
Тогда последовательность
в некотором смысле сходится (слабо сходится) к δ-функции.
Часто, в качестве
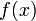 выбирают
выбираютдающую последовательность
Если нужно, чтобы члены последовательности были всюду положительными функциями, можно исходить из Гауссова колокола :
Интегральное представление
Во многих приложениях оказывается удобным интегральное представление дельта-функции:
ДоказательствоРассмотрим интеграл
 (1)
(1)
который можно интерпретировать как предел
где
 (2)
(2)
 График функции sin(x) / x
График функции sin(x) / xИзвестно, что
 (3)
(3)
В силу (3) для любого N справедливо равенство:
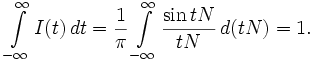 (4)
(4)
Можно показать (см. выше), что при неограниченном росте N для функции (2) оказываются верными все свойства дельта-функции и она в некотором смысле стремится к
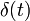 .
.Производная дельта-функции
Фундаментальное выражение, описывающее производную дельта-функции δ(x):
(распространение на случай подынтегральных выражений, содержащих дельта-функцию, интегрирования по частям).
Аналогично для n-ой производной дельта-функции:
А проинтегрировав так по частям n раз, получим в конце концов:
Подставив же в первую формулу f(x) = xg(x) и a = 0, убедимся, чтоДля производной дельта-функции также верны следующие тождества:
Преобразование Фурье
- В этом параграфе мы будем применять нормировку, соответствующую соглашению о единичном коэффициенте в обратном преобразовании, то есть имея в виду
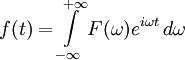 .
.
- Формулы этого параграфа имеют соответствующие аналоги для многомерного преобразования Фурье.
К дельта-функции можно применить преобразование Фурье:
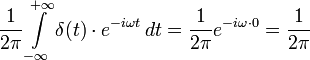 ,
,
в результате получается, что спектр (фурье-образ) δ-функции является просто константой:
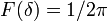 .
.
То есть, как и было показано выше,
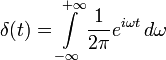 .
.
Представление многомерных дельта-функций в различных системах координат
В n-мерном пространстве в декартовых координатах (ортонормированном базисе):
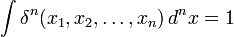 ;
;
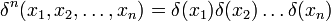 .
.
В двумерном пространстве:
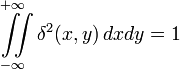 ;
;
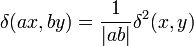 ;
;
- δ2(x,y) = δ(x)δ(y).
В полярных координатах:
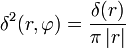 — несмещенная относительно начала координат (с особенностью при r = 0),
— несмещенная относительно начала координат (с особенностью при r = 0),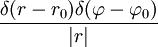 — с особенностью в точке общего положения
— с особенностью в точке общего положения 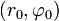 ; при r = 0 доопределяется нулем.
; при r = 0 доопределяется нулем.
В трехмерном пространстве:
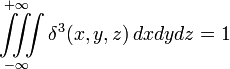 ;
;
- δ3(x,y,z) = δ(x)δ(y)δ(z);
В цилиндрической системе координат:
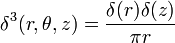 — несмещенная относительно начала координат (с особенностью при r = 0,z = 0),
— несмещенная относительно начала координат (с особенностью при r = 0,z = 0),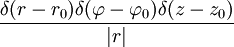 — с особенностью в точке общего положения
— с особенностью в точке общего положения 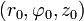 ; при r = 0 доопределяется нулем.
; при r = 0 доопределяется нулем.
В сферической системе координат:
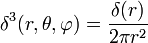 — несмещённая относительно начала координат (с особенностью при r = 0).
— несмещённая относительно начала координат (с особенностью при r = 0).
Физическая интерпретация
Вблизи заряжённой точки поле бесконечно, ряды Тейлора для поля не сходятся, поэтому вводят специальные функции. Одной из таких функций является дельта-функция. Вопрос о поле точечной заряженной частицы сравнительно сложен, поэтому рассмотрим сначала более простой пример.
Мгновенное ускорение
Пусть частица, движущаяся вдоль прямой, при ударе пренебрежимо малой длительности скачком приобретают какую-то скорость. Зададимся вопросом, как рассчитать ускорение, приобретенное телом? Построим график зависимости изменения скорости от времени. График будет иметь следующий вид:
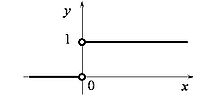
Данный график почти всюду является графиком функции Хевисайда. Производная функции Хевисайда является единичной дельта-функцией, график которой условно можно изобразить как
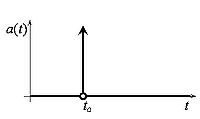
Данный график отображает бесконечное ускорение при мгновенном наборе скорости. В общем случае ускорение при ударе можно записать как
Масса материальной точки
Если нужно найти суммарную массу (или заряд) некоторого непрерывного распределения плотности (или плотности заряда)
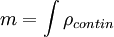 , содержащего кроме того точечные массы (заряды), то удобно вместо формулы, учитывающей отдельно дискретные массы и непрерывную конечную плотность:
, содержащего кроме того точечные массы (заряды), то удобно вместо формулы, учитывающей отдельно дискретные массы и непрерывную конечную плотность: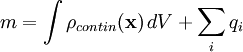
записывать просто:
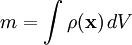
имея в виду, что
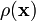 имеет как непрерывную, так и дельтообразные (по одной для каждой точечной массы) составляющие:
имеет как непрерывную, так и дельтообразные (по одной для каждой точечной массы) составляющие: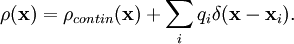
Другие примеры
- Дельта-функция применяется в математической физике при решении задач, в которые входят сосредоточенные величины. В квазиклассическом пределе (
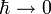 ) квантовой механики волновые функции локализуются в волновые пакеты с дельтаобразными (то есть имеющими в пределе форму дельта-функции) огибающими, и области их локализации движутся по классическим траекториям согласно уравнениям Ньютона.
) квантовой механики волновые функции локализуются в волновые пакеты с дельтаобразными (то есть имеющими в пределе форму дельта-функции) огибающими, и области их локализации движутся по классическим траекториям согласно уравнениям Ньютона.
- Преобразование Фурье синуса является дельта-функцией. Это позволяет более удобно и математически строго формулировать различные задачи, связанные с преобразованием Фурье, которые очень многочисленны: волновая оптика, акустика, теория колебаний. В квантовой механике преобразования Фурье волновых функций играют первостепенную принципиальную и техническую роль, именно для неё Дирак впервые ввёл дельта-функцию.
- Дельта-функции играют роль собственных функций оператора с непрерывным спектром в представленииях, где этот оператор диагонален. Таким образом, они играют роль базиса в диагональном представлении оператора.
- Важным применением дельта-функции является их участие в аппарате функций Грина линейных операторов. Для линейного оператора L, действующего на обобщённые функции над многообразием M, уравнение, определяющее функцию Грина g с источником в точке x0, имеет вид
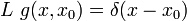 .
.
- Особенно часто встречается применение этого аппарата к оператору Лапласа (электростатика, теплопроводность, диффузия, механическая теория упругости) и подобным ему операторам, таким как оператор Даламбера (акустика, электродинамика, квантовая теория поля, где функция Грина часто носит специальное название пропагатора).
- Для лапласиана в
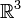 функцией Грина является функция 1 / r, так что
функцией Грина является функция 1 / r, так что
- где r — расстояние до начала координат. Этот факт используется для доказательства того, что выражение для скалярного потенциала:
- удовлетворяет уравнению Пуассона:
Литература
- Дирак П. А. М. Основы квантовой механики, пер. с англ., — М., 1932 (есть много переизданий).
Ссылки
- Кудрявцев Л. Д. Краткий курс математического анализа, том 2, — ISBN 5-9221-0185-4
- Weisstein, Eric W. Delta Function на сайте Wolfram MathWorld.(англ.)
См. также
Wikimedia Foundation. 2010.

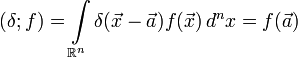

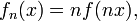
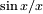
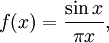
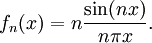
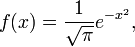
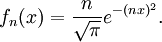
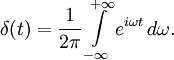
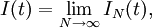
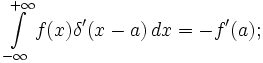
![\int\limits_{-\infty}^{+\infty} f(x)\delta^{[n]}(x-a)\,dx
= -\int\limits_{-\infty}^{+\infty}\frac{\partial f}{\partial x}\delta^{[n-1]}(x-a)\,dx.](/pictures/wiki/files/99/cdc4c03773824d3ab6bf4503cca23e62.png)
![\int\limits_{-\infty}^{+\infty} f(x)\delta^{[n]}(x-a)\,dx = \left.(-1)^{n} \frac{\partial^{n} f(x)}{\partial x^{n}}\right|_{x=a}.](/pictures/wiki/files/54/642c2fcb67ab707b77641b20c9b6cb2e.png)