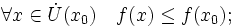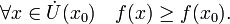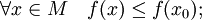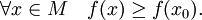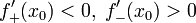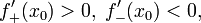Локальный минимум

Экстре́мум (лат. extremum — крайний) в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. В математическом анализе выделяют также понятие локальный экстремум (соответственно минимум или максимум).

Определения

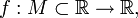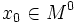Пусть дана функция $f:M \subset \R \to \R,$ и $x_0 \in M^0$ — внутренняя точка области определения f. Тогда

• x₀ называется точкой локального максимума функции f, если существует проколотая окрестность 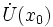$\dot{U}(x_0)$ такая, что

  $\forall x \in \dot{U}(x_0) \quad f(x) \le f(x_0);$

• x₀ называется точкой локального минимума функции f, если существует проколотая окрестность 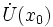$\dot{U}(x_0)$ такая, что

  $\forall x \in \dot{U}(x_0) \quad f(x) \ge f(x_0).$

Если неравенства выше строгие, то x₀ называется точкой строгого локального максимума или минимума соответственно.

• x₀ называется точкой абсолютного (глобального) максимума, если

  $\forall x\in M\quad f(x) \le f(x_0);$

• x₀ называется точкой абсолютного минимума, если

  $\forall x\in M\quad f(x) \ge f(x_0).$

Значение функции f(x₀) называют (строгим) (локальным) максимумом или минимумом в зависимости от ситуации. Точки, являющиеся точками (локального) максимума или минимума, называются точками (локального) экстремума.

Замечание

Функция f, определённая на множестве M, может не иметь на нём ни одного локального или абсолютного экстремума. Например, $f(x) = x,\; x\in (-1,1).$

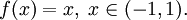
Необходимые условия существования локальных экстремумов

• Лемма Ферма. Пусть функция 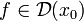$f\in \mathcal{D}(x_0)$ дифференцируема в точке локального экстремума x₀. Тогда:

f'(x₀) = 0.

Достаточные условия существования локальных экстремумов

• Пусть функция 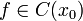$f\in C(x_0)$ непрерывна в 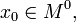$x_0\in M^0,$ и существуют конечные или бесконечные односторонние производные 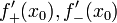$~f'_+(x_0), f'_-(x_0)$. Тогда при условии

$f'_+(x_0) < 0,\; f'_-(x_0) > 0$

x₀ является точкой строгого локального максимума. А если

$f'_+(x_0) > 0,\; f'_-(x_0) < 0,$

то x₀ является точкой строгого локального минимума.

Заметим, что при этом функция не дифференцируема в точке x₀

• Пусть функция f непрерывна и дважды дифференцируема в точке x₀. Тогда при условии

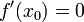$~f'(x_0)=0$ и $~f''(x_0) < 0$

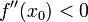
x₀ является точкой локального максимума. А если

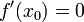$~f'(x_0)=0$ и $~f''(x_0) > 0$

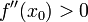
то x₀ является точкой локального минимума.

См. также

• Критическая точка (математика)
• Точная верхняя и нижняя грань
• Максимум
• Методы оптимизации
• Условный экстремум