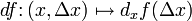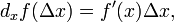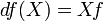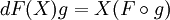- Полный дифференциал
-
Дифференциа́л в математике — линейная часть приращения функции или отображения. Это понятие тесно связанное с понятием производной по направлению.
Обычно дифференциал f обозначается df, а его значение в точке x обозначается dxf.
Содержание
Неформальное описание
Рассмотрим гладкую функцию f(x). Проведем касательную к ней в точке x, и отложим на этой касательной отрезок, такой длины, чтобы его проекция на ось x была равна Δx. Проекция этого отрезка на ось y называется дифференциалом функции f(x) в точке x от Δx. Таким образом, дифференциал может пониматься как функция двух переменных x и Δx,
определяемой соотношением
в частности, разность приращения функции и её дифференциала — бесконечно малая величина:
- f(x + Δx) = f(x) + dxf(Δx) + o(Δx).
Определения
Для функций
Дифференциал гладкой вещественнозначной функции f определённой на M (M — область в
 или гладкое многообразие) представляет собой 1-форму и обычно обозначается df и определяется соотношением
или гладкое многообразие) представляет собой 1-форму и обычно обозначается df и определяется соотношениемгде
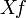 обозначает производную f по направлению вектора X в касательном расслоении M.
обозначает производную f по направлению вектора X в касательном расслоении M.Для отображений
Дифференциал гладкого отображения из гладкого многообразия в многообразие
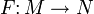 есть отображение между их касательными расслоениями,
есть отображение между их касательными расслоениями, 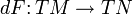 , такое что для любой гладкой функции
, такое что для любой гладкой функции 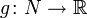 имеем
имеемгде Xf обозначает производную f по направлению X. (В левой части равенства берётся производная в N функции g по dF(X) в правой — в M функции
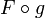 по X).
по X).Это понятие естественно обобщает дифференциал функции.
Связанные определения
- Гладкое отображение
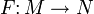 называется субмерсией, если для любой точки
называется субмерсией, если для любой точки 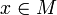 , дифференциал
, дифференциал 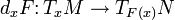 сюръективен.
сюръективен. - Гладкое отображение
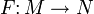 называется гладким погружением, если для любой точки
называется гладким погружением, если для любой точки 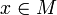 , дифференциал
, дифференциал 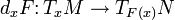 инъективен.
инъективен.
Свойства
- Дифференциал композиции равен композиции дифференциалов:
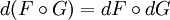 или
или 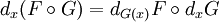
Примеры
- Пусть в открытом множестве
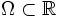 задана гладкая функция
задана гладкая функция 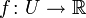 . Тогда df = f'dx, где f' обозначает производную f, а dx является постоянной формой определяемой dx(V) = V.
. Тогда df = f'dx, где f' обозначает производную f, а dx является постоянной формой определяемой dx(V) = V. - Пусть в открытом множестве
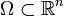 задана гладкая функция
задана гладкая функция 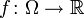 . Тогда
. Тогда 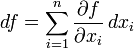 . Форма dxi может быть определена соотношением dxi(V) = vi, для вектора
. Форма dxi может быть определена соотношением dxi(V) = vi, для вектора 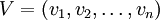 .
. - Пусть в открытом множестве
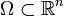 задано гладкое отображение
задано гладкое отображение 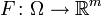 . Тогда
. Тогда
dxF(v) = J(x)v,
где J(x) есть матрица Якоби отображения F в точке x.
История
Термин Дифференциал (от лат. differentia — разность, различие) введён Лейбницем. Изначально, dx применялось для обозначения «бесконечно малой» — величины, которая меньше всякой конечной величины и всё же не равна нулю. Подобный взгляд оказался неудобным в большинстве разделов математики (за исключением нестандартного анализа).
См. также
Wikimedia Foundation. 2010.