Признаки подобия треугольников
- Признаки подобия треугольников
-
Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного пропорциональны сходственным сторонам другого.
Признаки подобия треугольников
Признаки подобия треугольников — геометрические признаки, позволяющие установить, что два треугольника являются подобными без использования всех элементов.
Первый признак
|
Если два угла одного треугольника соответственно равны двум углам другого, то треугольники подобны.
|
Дано: ∆ABC и ∆A1B1C1, ∠A=∠A1, ∠B=∠B1.
Доказать: ∆ABC 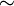 ∆A1B1C1.
∆A1B1C1.
Второй признак
|
Если две стороны одного треугольника пропорциональны двум сторонам другого и углы между этими сторонами равны, то треугольники подобны.
|
Дано: ∆ABC и ∆A1B1C1, ∠A=∠A1, 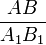 =
= 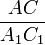 .
.
Доказать: ∆ABC 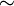 ∆A1B1C1.
∆A1B1C1.
Третий признак
|
Если три стороны одного треугольника пропорциональны трем сходственным сторонам другого, то треугольники подобны.
|
Дано: ∆ABC и ∆A1B1C1, 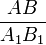 =
= 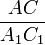 =
= 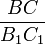 .
.
Доказать: ∆ABC  ∆A1B1C1.
∆A1B1C1.
Доказательство
1) Рассмотрим ∆ABC2, в котором ∠BAC2=∠A1 и ∠ABC2=∠B1:
∆ABC2 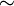 ∆A1B1C1 (первый признак) =>
∆A1B1C1 (первый признак) => 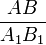 =
= 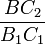 =
= 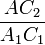 .
.
2) По условию:
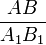
=
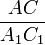
=
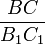
=> AC=AC
2, BC=BC
2 => ∆ABC = ∆ABC
2 (
третий признак);
∆ABC
2 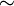
∆A
1B
1C
1 => ∆ABC
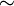
∆A
1B
1C
1.
Теорема доказана.
- По острому углу — см. первый признак;
- По двум катетам — см. второй признак;
- По катету и гипотенузе — см. второй признак.
Свойства подобных треугольников
Треугольники, на которые высота, опущенная из прямого угла, делит прямоугольный треугольник, подобны всему треугольнику по первому признаку, а значит:
- Высота прямоугольного треугольника, опущенная на гипотенузу, равна среднему геометрическому проекций катетов на гипотенузу,
- Катет равен среднему геометрическому гипотенузы и проекции этого катета на гипотенузу.
Связанные определения
- Коэффициент подобия — число k, равное отношению сходственных сторон подобных треугольников.
- Сходственные стороны подобных треугольников — стороны, лежащие напротив равных углов.
Литература
- Геометрия 7-9/Л. С. Атанасян и др. — 12-е изд. — М.: Просвещение, 2002. — 384 c.: ил.
См. также
Ссылки
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое "Признаки подобия треугольников" в других словарях:
Признаки равенства треугольников — Стандартные обозначения Треугольник простейший многоугольник, имеющий 3 вершины (угла) и 3 стороны; часть плоскости, ограниченная тремя точками, не лежащими на одной прямой, и тремя отрезками, попарно соединяющими эти точки. Вершины треугольника … Википедия
Подобие треугольников — Признаки подобия треугольников геометрические признаки, позволяющие установить, что два треугольника являются подобными без использования всех элементов. Содержание 1 Признаки подобия треугольников 1.1 Первый признак … Википедия
Преобразование подобия — Подобие преобразование евклидова пространства, при котором для любых двух точек A, B и их образов A , B имеет место соотношение | A B | = k | AB | , где k положительное число, называемое коэффициентом подобия. Содержание 1 Примеры 2 Связанны … Википедия
Подобные треугольники — Подобные треугольники треугольники, у которых углы соответственно равны, а стороны одного пропорциональны сходственным сторонам другого. Содержание 1 Признаки подобия треугольников 1.1 Первый признак … Википедия
Треугольник — У этого термина существуют и другие значения, см. Треугольник (значения). Треугольник (в евклидовом пространстве) это геометрическая фигура, образованная тремя отрезками, которые соединяют три не лежащие на одной прямой точки. Три точки,… … Википедия
Подобие — У этого термина существуют и другие значения, см. Подобие (значения). Подобие преобразование евклидова пространства, при котором для любых двух точек , и их образов , имеет место соотношение , где положительное число, называемое… … Википедия
Подобные фигуры — Подобие преобразование евклидова пространства, при котором для любых двух точек A, B и их образов A , B имеет место соотношение | A B | = k | AB | , где k положительное число, называемое коэффициентом подобия. Содержание 1 Примеры 2 Связанны … Википедия
подобие — я; ср. 1. Пренебр. Нечто похожее, сходное с чем л. Жалкое п. старинного полонеза. П. человеческой фигуры. Не Гамлет, а его бесконечные подобия. Лепить по своему подобию (влияя на кого л., воспитывая кого л., делать его похожим на себя). 2. Матем … Энциклопедический словарь
Площадь треугольника — Стандартные обозначения Треугольник простейший многоугольник, имеющий 3 вершины (угла) и 3 стороны; часть плоскости, ограниченная тремя точками, не лежащими на одной прямой, и тремя отрезками, попарно соединяющими эти точки. Вершины треугольника … Википедия
подобие — я; ср. 1) пренебр. Нечто похожее, сходное с чем л. Жалкое подо/бие старинного полонеза. Подо/бие человеческой фигуры. Не Гамлет, а его бесконечные подобия. Лепить по своему подобию (влияя на кого л., воспитывая кого л., делать его похожим на… … Словарь многих выражений
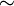 ∆A1B1C1.Доказательство
∆A1B1C1.Доказательство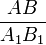 =
= 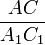 .
.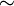 ∆A1B1C1.Доказательство
∆A1B1C1.Доказательство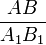 =
= 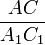 =
= 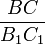 .
. ∆A1B1C1.Доказательство
∆A1B1C1.Доказательство
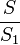 =
= 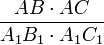 =
= 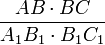 =>
=> 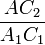 .
.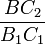 =
=