Подобные фигуры

Подобие — преобразование евклидова пространства, при котором для любых двух точек A, B и их образов A', B' имеет место соотношение | A'B' | = k | AB | , где k — положительное число, называемое коэффициентом подобия.

Примеры

• Каждая гомотетия является подобием.
• Каждое движение (в том числе и тождественное) также можно рассматривать как преобразование подобия с коэффициентом k = 1.

Подобные фигуры на рисунке имеют одинаковые цвета.

Связанные определения

• Фигура F называется подобной фигуре F', если существует преобразование подобия, при котором $F\to F'$.
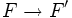  • Подобие фигур является отношением эквивалентности.

Свойства

• Подобие есть взаимно однозначное отображение евклидова пространства на себя.
• Подобие сохраняет порядок точек на прямой, то есть если точка B лежит между точками A, C и B', A', C' — соответствующие их образы при некотором подобии, то B' также лежит между точками A' и C'.
• Точки, не лежащие на прямой, при любом подобии переходят в точки, не лежащие на одной прямой.
• Подобие преобразует прямую в прямую, отрезок в отрезок, луч в луч, угол в угол, окружность в окружность.
• При подобии угол сохраняет величину.
• Подобие с коэффициентом 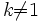$k\not=1$, преобразующее каждую прямую в параллельную ей прямую, является гомотетией с коэффициентом k или − k.
  • Каждое подобие можно рассматривать как композицию движения D и некоторой гомотетии Γ с положительным коэффициентом.
  • Подобие называется собственным (несобственным), если движение D является собственным (несобственным). Собственное подобие сохраняет ориентацию фигур, а несобственное — изменяет ориентацию на противоположную.
• Два треугольника являются подобными, если
  • их соответственные углы равны, или
  • стороны пропорциональны. См. также Признаки подобия треугольников.
• Площади подобных фигур пропорциональны квадратам их сходственных линий (например, сторон). Так, площади кругов пропорциональны отношению квадратов их диаметров (или радиусов).

Обобщения

Аналогично определяется подобие (с сохранением указанных выше свойств) в 3-мерном евклидовом пространстве, а также в n-мерном евклидовом и псевдоевклидовом пространствах.

В метрических пространствах так же, как в n-мерных римановых, псевдоримановых и финслеровых пространствах подобие определяется как преобразование, переводящее метрику пространства в себя с точностью до постоянного множителя.

Совокупность всех подобий n-мерного евклидова, псевдоевклидова, риманова, псевдориманова или финслерова пространства составляет r-членную группу преобразований Ли, называемой группой подобных (гомотетических) преобразований соответствующего пространства. В каждом из пространств указанных типов r-членная группа подобных преобразований Ли содержит (r − 1)-членную нормальную подгруппу движений.

См. также

• Конгруэнтность (геометрия)
• Конформное отображение
• Признаки подобия треугольников