- Тетрация
-
Тетрация (гипероператор-4) в математике — итерационная функция экспоненты, следующий гипероператор после возведения в степень. Тетрация используется для описания больших чисел.
Термин «тетрация», состоящий из слов «тетра-» (четыре) и «итерация» (повторение), был впервые применён английским математиком Рубеном Гудстейном (англ.) в 1947 году[1].
Содержание
Определения
Тетрация как степенная башня
Для любого положительного вещественного числа
 и неотрицательного целого числа
и неотрицательного целого числа  , тетрацию
, тетрацию  можно определить рекуррентно:
можно определить рекуррентно: (если
(если  )
) (если
(если  )
)
Согласно данному определению, вычисление тетрации, записанной как «степенная башня», возведение в степень начинается с самых дальних уровней к начальному (в данной системе обозначений, с самого наивысшего показателя степени):
При этом, так как возведение в степень не является ассоциативной операцией, то вычисление выражения в другом порядке приведёт к другому ответу:
Таким образом, степенные башни должны вычисляться сверху-вниз (или справа-налево), то есть, иначе говоря, они обладают правой ассоциативностью.
Тетрация как гипероператор
Тетрация является четвёртой по счёту гипероперацией:
- сложение:
- умножение:
- возведение в степень:
- тетрация:
Здесь каждая операция является итерацией предыдущей.
Свойства
- В отличие от трёх первых гиперопераций (сложения, умножения и возведения в степень), которые допускают аналитическое продолжение на всю комплексную плоскость (то есть имеют смысл при комплексных значениях
 ), для тетрации такого продолжения построить не удаётся.
), для тетрации такого продолжения построить не удаётся. - Тетрация не считается элементарной функцией.
- В силу некоммутативности тетрация имеет две обратных операции — суперлогарифм и суперкорень.
Терминология
Существует несколько терминов для определения понятия тетрация и за каждым из них стоит своя логика, но некоторые из них не стали общепринятыми в силу тех или иных причин. Ниже приведено несколько подобных примеров.
- Термин «тетрация», использованный Рубеном Гудстейном в 1947 году в работе «Transfinite Ordinals in Recursive Number Theory» (обобщение рекуррентных представлений в теореме Гудстейна, используемых для высших операторов), имеет доминирующее положение в терминологии. Также этот термин был популяризован в работе Руди Руккера (англ. Rudy Rucker) «Infinity and the Mind».
- Термин «супервозведение в степень» (англ. superexponentiation) был опубликован Бромером (англ. Bromer) в его работе «Superexponentiation» в 1987 году.[2] Данный термин был ранее использован Эдом Нельсоном (англ. Ed Nelson) в своей книге «Предикативная Арифметика» (англ. «Predicative Arithmetic»)[3].
- Термин «гиперстепень» (англ. hyperpower)[4] есть естественная комбинация понятий «гипер-» и «степень», который подходящим образом описывает тетрацию. Проблема лежит в понятии самого термина «гипер» относительно иерархии гипероператоров. Когда мы рассматриваем гипероператоры, термин «гипер» относится ко всем рангам, а термин «супер» относится к рангу 4, или тетрации. Таким образом, при данных обстоятельствах, понятие «гиперстепень» может ввести в заблуждение, так как оно относится только к понятию тетрация.
- Термин «степенная башня» (англ. power tower)[5] иногда используется, в форме «степенная башня порядка
 » для
» для  .
.
Тетрацию также часто путают с другими тесно связанными функциями и выражениями. Ниже приведено несколько связанных терминов:
-
Форма Терминология 
Тетрация 
Итерационные экспоненты 
Вложенные экспоненты (также башни) 
Бесконечные экспоненты (также башни)
В первых двух выражениях
 есть основание, и количество появляющихся
есть основание, и количество появляющихся  есть высота. В третьем выражении,
есть высота. В третьем выражении,  есть высота, но все основания разные.
есть высота, но все основания разные.Обозначения
Системы записи в которых тетрация может быть использована (некоторые из них позволяют использование даже более высоких итераций) включают в себя:
-
Имя Форма Описание Стандартная форма записи 
Использована Мауером (Maurer) [1901] и Гудштейном [1947]; популяризовано в книге Руди Рюкера «Infinity and the Mind». Стрелочная нотация Кнута 
Позволяет удлинение путём добавление добавочных или индексированных стрелочек, является более мощным способом. Цепочка Конвея 
Позволяет удлинение путём прибавления 2 (эквивалентно вышеописанному способу), но также возможно даже более мощный способ записи, если увеличивать цепочку Функция Аккермана 
Допускает особый случай  в записи в терминах функции Аккермана.
в записи в терминах функции Аккермана.Итерируемая экспоненциальная форма записи 
Позволяет простое удлинение до итерационных экспонент начиная со значений отличных от 1. Обозначения Хусменд (англ. Hooshmand) [6] 
Система записи гипероператорами 
Позволяет удлинение путём прибавления 4; это даёт семейство гипероператоров. Система записи ASCII a^^nТак как запись стрелочка наверх используется идентично обозначению корректурного знак вставки ( ^), оператор тетрация может быть записан в виде (^^).Нотация массивов Бауэрса {a,b,2} {a,b,c} = a^^^...^^^b (c стрелок сверхстепени).
Одна из вышеприведённых систем использует систему записи итерированных экспонент; в общем случае это определяется следующим образом:
Не так много обозначений существует для итерированных экспонент, но несколько из них показаны ниже:
-
Имя Форма Описание Стандартная форма записи 
Система записи  и итерационная система записи
и итерационная система записи  была введена Эйлером.
была введена Эйлером.Стрелочная нотация Кнута 
Позволяет для суперстепеней и суперэкспоненциальных функций увеличивать число стрелочек. Гипер-Е нотация E(a)x#n Система записи Иоанна Галидакиса (англ. Ioannis Galidakis) 
Допускает использование больших выражений в основании.[7] ASCII (добавочный) a^^n@xОснована на взгляде, что итерационная экспонента есть добавочная тетрация. ASCII (стандартный) exp_a^n(x)Основана на стандартной форме записи.
Примеры
В нижеприведённой таблице большинство значений слишком огромны, чтобы их записать в экспоненциальном представлении, по этой причине используется система записи в виде итерационных экспонент, чтобы представить их с основанием 10. Значения, содержащие десятичную запятую, являются приблизительными.
-




1 1 1 1 2 4 16 65 536 3 27 7 625 597 484 987 
4 256 

5 3 125 

6 46 656 

7 823 543 

8 16 777 216 

9 387 420 489 

10 10 000 000 000 

Открытые проблемы
- Неизвестно, являются ли nπ или ne целыми числами при каком-либо положительном целом n. Неизвестно даже, является ли
 целым.
целым.
См. также
Примечания
- ↑ Goodstein R. L. (1947). «Transfinite ordinals in recursive number theory». Journal of Symbolic Logic 12. DOI:10.2307/2266486.
- ↑ Bromer N. (1987). «Superexponentiation». Mathematics Magazine 60 (3): 169–174.
- ↑ Nelson E. Predicative Arithmetic. — Princeton University Press, 1986.
- ↑ MacDonnell J. F. (1989). «Somecritical points of the hyperpower function
 ». International Journal of Mathematical Education 20 (2): 297–305. MR994348.
». International Journal of Mathematical Education 20 (2): 297–305. MR994348. - ↑ Weisstein, Eric W. Power Tower (англ.) на сайте Wolfram MathWorld.
- ↑ Hooshmand M. H. (2006). «Ultra power and ultra exponential functions». Integral Transforms and Special Functions 17 (8): 549–558. DOI:10.1080/10652460500422247.
- ↑ Galidakis I. On Extending hyper4 and Knuth’s Up-arrow Notation to the Reals.
Ссылки
- Сайт про тетрацию Эндрю Робинса.
- Сайт про тетрацию Даниэля Гэйслера.
- Форум по обсуждению тетрации.
- Кузнецов Д. Тетрация как специальная функция // Владикавказский математический журнал. — 2010.
 Категория:
Категория:- Математические операции
Wikimedia Foundation. 2010.



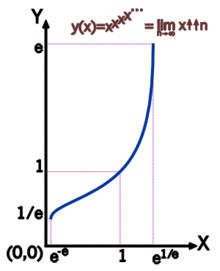
 . Бесконечное возведение в степень для основания
. Бесконечное возведение в степень для основания  .
.



