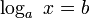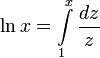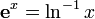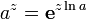- Показатель степени
-
Число ab называется степенью с основанием a и показателем b.
Содержание
Натуральная степень
Число с называется n-ной степенью числа а, если
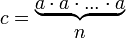 .
.Свойства:
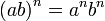
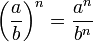
- anam = an + m
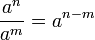 , n>m.
, n>m.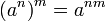
Существует алгоритм быстрого возведения в степень, выполняющий возведение в степень за меньшее, чем в определении, число умножений.
Целая степень
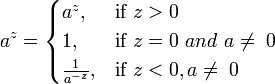
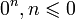 не определён
не определёнРациональная степень
По определению,
![a^{p\over q} = \sqrt[q]{a^p}, \quad p \in \mathbb{Z}\ , q \in \mathbb{N}\](/pictures/wiki/files/98/ba5ef381235aee96027fbe5e876d0d3e.png)
См. корень степени q
Действительная степень
Пусть
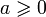 .
.В школе действительную функцию вводят, используя тот факт, что между любыми двумя рациональными числами существует иррациональное, а между любыми двумя иррациональными — рациональное. Тогда
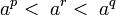 , где p < q, | p − q | < ε, где ε — погрешность вычисления. Таким образом, для любого иррационального числа r подбираются два рациональных p и q с необходимой степенью точности и любое число между ap и aq принимается за ответ.
, где p < q, | p − q | < ε, где ε — погрешность вычисления. Таким образом, для любого иррационального числа r подбираются два рациональных p и q с необходимой степенью точности и любое число между ap и aq принимается за ответ.Другой подход основан на теории рядов и логарифмов. (см. определение комплексной степени)
Потенцирование
Потенцирование — это нахождение числа по известному значению его логарифма, то есть решение уравнения:
Из определения логарифма вытекает, что x = ab. Таким образом, потенцирование означает возведение основания логарифма в степень, равную значению логарифма. Например, если десятичный логарифм числа равен L, то искомое число равно 10L.
Комплексная степень
Определим некоторые функции:
теперь для вычисления az можно использовать свойства степеней и логарифмов:
Степень как функция
Поскольку в выражении xy принимает участие две переменных, то его можно рассматривать как:
- функцию переменной x (при этом y — параметр). Такая функция называется степенной. Это — частный случай полиномиальной функции.
- функцию переменной y (при этом x — параметр). Такая функция называется показательной. Её частный случай — экспонента.
- функцию двух переменных.
См. также
- e (математическая константа)
- Логарифм — обратная к возведению в степень функция.
- Корень n-й степени — обратная к возведению в степень функция.
- Квадрат — возведение во вторую степень.
- Куб — возведение в третью степень.
- Тетрация — обобщение возведения в степень.
- Гипероператор
Ссылки
- А. Б. Будак, Б. М. Щедрин «Элементарная математика» — Подготовка к вступительным экзаменам в МГУ
Wikimedia Foundation. 2010.