Функция Эйри

График функций Ai(x) (красный) и Bi(x) (синий).

Функция Эйри $\operatorname{Ai}\,(x)$ — специальная функция, названная в честь британского астронома Джорджа Бидделя Эйри. Функции $\operatorname{Ai}\,(x)$ и связанная с ней $\operatorname{Bi}\,(x)$, называемая также функцией Эйри, являются линейно независимыми решениями дифференциального уравнения

$y'' - xy = 0$,

называемого уравнением Эйри. Это простейшее дифференциальное уравнение, имеющее точку, в которой вид решения меняется с колеблющегося на экспоненциальный.

Функция Эйри описывает вид звезды (точечного источника света) в телескопе. Идеальная точка превращается в набор концентрических окружностей, в силу ограниченной апертуры и волновой природы света (Suiter 1994). Она также является решением уравнения Шрёдингера для частицы в треугольной потенциальной яме.

Определение

Для вещественных $x$, функция Эйри определяется интегралом

$\operatorname{Ai}\,(x) = \frac{1}{\pi} \int\limits_0^\infty\!\cos\left(\frac{t^3}{3} + xt\right)\, dt.$

взятом в несобственном смысле. Легко проверить, что он действительно сходится.

Выполняя дифференцирование под знаком интеграла, убеждаемся, что полученная функция действительно удовлетворяет уравнению Эйри.

$y'' - xy = 0 .$

У этого уравнения есть два линейно независимых решения. Вторым решением обычно берут функцию Эйри второго рода, обозначаемую $\operatorname{Bi}\,(x)$. Она определяется как решение с той же амплитудой колебаний, что и $\operatorname{Ai}\,(x)$, при стремлении $x \to \infty$, и отличающееся по фазе на $\pi/2$.

Для комплексных чисел функция Эйри определяется следующим образом:

$\operatorname{Ai}\,(z) = \int\limits_{\gamma_k}\!\exp \left(pz - \frac{p^3}{3}\right)\,dp$

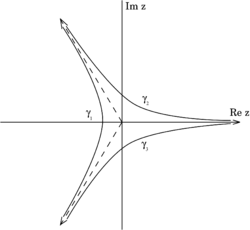
где контур $\gamma_k$ может быть одним из представленных на рисунке. Несмотря на то, что существует три контура интегрирования, решений уравнения Эйри остается по прежнему два, так как сумма интегралов по этим трем контурам равна нулю.

Свойства

В точке $x=0$ функции $\operatorname{Ai}\,(x)$ и $\operatorname{Bi}\,(x)$ и их производные имеют значения

$\begin{align} \operatorname{Ai}\,(0) &{}= \frac{1}{3^{2/3}\Gamma\left(\frac23\right)}, & \quad \operatorname{Ai}'\,(0) &{}= -\frac{1}{3^{1/3}\Gamma\left(\frac13\right)}, \\ \operatorname{Bi}\,(0) &{}= \frac{1}{3^{1/6}\Gamma\left(\frac23\right)}, & \quad \operatorname{Bi}'\,(0) &{}= \frac{3^{1/6}}{\Gamma\left(\frac13\right)}. \end{align}$

где $\Gamma$ — гамма-функция. Отсюда следует, что вронскиан функций $\operatorname{Ai}\,(x)$ и $\operatorname{Bi}\,(x)$ равен $1/\pi$.

При положительных $x$ $\operatorname{Ai}\,(x)$ — положительная, выпуклая функция, убывающая экспоненциально к 0, а $\operatorname{Bi}\,(x)$ — положительная, выпуклая функция, возрастающая экспоненциально. При отрицательных $x$ $\operatorname{Ai}\,(x)$ и $\operatorname{Bi}\,(x)$ колеблются вокруг нуля с возрастающей частотой и убывающей амплитудой. Это подтверждается асимптотическими выражениями для функций Эйри.

Асимптотические выражения

При x стремящемся к +∞:

$\begin{align} \mathrm{Ai}(x) &{}\sim \frac{e^{-\frac23x^{3/2}}}{2\sqrt\pi\,x^{1/4}} \\ \mathrm{Bi}(x) &{}\sim \frac{e^{\frac23x^{3/2}}}{\sqrt\pi\,x^{1/4}}. \end{align}$

$\begin{align} \mathrm{Ai}(-x) &{}\sim \frac{\sin(\frac23x^{3/2}+\frac14\pi)}{\sqrt\pi\,x^{1/4}} \\ \mathrm{Bi}(-x) &{}\sim \frac{\cos(\frac23x^{3/2}+\frac14\pi)}{\sqrt\pi\,x^{1/4}}. \end{align}$

Комплексный аргумент

Функция Эйри может быть продолжена на комплексную плоскость по формуле

$\mathrm{Ai}(z) = \frac{1}{2\pi i} \int\limits_{C} \exp\left(\frac{t^3}{3} - zt\right)\, dt,$

где интеграл берется по контуру $C$, начинающемуся в точке на бесконечности с аргументом -π/3 и заканчивающимся в точке на бесконечности с аргументом π/3. Можно пойти с другой стороны, использую дифференциальное уравнение $y'' - xy = 0$ для продолжения Ai(x) и Bi(x) до целых функций на комплексной плоскости.

Асимптотическая формула для Ai(x) остается в силе на комплексной плоскости, если брать главное значение x^2/3 и x не лежит на отрицательной вещественной полуоси. Формула для Bi(x) верна, если x лежит в секторе {x∈C : |arg x| < (1/3)π−δ} для некоторого положительного δ. Формулы для Ai(−x) и Bi(−x) верны, если x лежит в секторе {x∈C : |arg x| < (2/3)π−δ}.

Из асимптотического поведения функций Эйри следует, что они обе имеют бесконечно много нулей на отрицательной вещественной полуоси. У функции Ai(x) на комплексной плоскоти нет других нулей, а функция Bi(x) имеет бесконечно много нулей в секторе {z∈C : (1/3)π < |arg z| < (1/2)π}.

Связь с другими специальными функциями

Для положительных аргументов, функции Эйри связаны с модифицированными функциями Бесселя:

$\begin{align} \mathrm{Ai}(x) &{}= \frac1\pi \sqrt{\frac13 x} \, K_{1/3}\left(\frac23 x^{3/2}\right), \\ \mathrm{Bi}(x) &{}= \sqrt{\frac13 x} \left(I_{1/3}\left(\frac23 x^{3/2}\right) + I_{-1/3}\left(\frac23 x^{3/2}\right)\right). \end{align}$

где I_±1/3 и K_1/3 — решения уравнения $x^2y'' + xy' - (x^2 + 1/9)y = 0$.

Для отрицательных аргументов функции Эйри связаны с функциями Бесселя:

$\begin{align} \mathrm{Ai}(-x) &{}= \frac13 \sqrt{x} \left(J_{1/3}\left(\frac23 x^{3/2}\right) + J_{-1/3}\left(\frac23 x^{3/2}\right)\right), \\ \mathrm{Bi}(-x) &{}= \sqrt{\frac13 x} \left(J_{-1/3}\left(\frac23 x^{3/2}\right) - J_{1/3}\left(\frac23 x^{3/2}\right)\right). \end{align}$

где J_±1/3 — решения уравнения $x^2y'' + xy' + (x^2 - 1/9)y = 0$.

Функции Скорера являются решениями уравнения $y'' - xy = 1/\pi$. Они также могут быть выражены через функции Эйри:

$\begin{align} \mathrm{Gi}(x) &{}= \mathrm{Bi}(x) \int\limits_x^\infty \mathrm{Ai}(t) \, dt + \mathrm{Ai}(x) \int\limits_0^x \mathrm{Bi}(t) \, dt, \\ \mathrm{Hi}(x) &{}= \mathrm{Bi}(x) \int\limits_{-\infty}^x \mathrm{Ai}(t) \, dt - \mathrm{Ai}(x) \int\limits_{-\infty}^x \mathrm{Bi}(t) \, dt. \end{align}$

История

Функция Эйри названа в честь британского астронома Джоржда Бидделля Эйри, который столкнулся с ней в исследованиях по оптике (1838 г.). Обозначение Ai(x) было введено Гарольдом Джеффри.

Ссылки

• Weisstein, Eric W. Airy Functions (англ.) на сайте Wolfram MathWorld.
• Chapter AI: Airy and related functions in the Digital library of mathematical functions.

См. также

• Луч Эйри

Литература

• Ландау, Л. Д., Лифшиц, Е. М. Квантовая механика (нерелятивистская теория). — Издание 4-е. — М.: Наука, 1989. — 768 с. — («Теоретическая физика», том III). — ISBN 5-02-014421-5 — математические дополнения, 749
• Milton Abramowitz and Irene A. Stegun (1954). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, (См. § 10.4).
• Airy (1838). On the intensity of light in the neighbourhood of a caustic. Transactions of the Cambridge Philosophical Society, 6, 379—402.
• Olver (1974). Asymptotics and Special Functions, Chapter 11. Academic Press, New York.