- Функции Бесселя
-
Функции Бесселя в математике — семейство функций, являющихся каноническими решениями дифференциального уравнения Бесселя:
где
 — произвольное вещественное число, называемое порядком.
— произвольное вещественное число, называемое порядком.Наиболее часто используемые функции Бесселя — функции целых порядков.
Хотя
 и
и  порождают одинаковые уравнения, обычно договариваются о том, чтобы им соответствовали разные функции (это делается, например, для того, чтобы функция Бесселя была гладкой по
порождают одинаковые уравнения, обычно договариваются о том, чтобы им соответствовали разные функции (это делается, например, для того, чтобы функция Бесселя была гладкой по  ).
).Функции Бесселя впервые были определены швейцарским математиком Даниилом Бернулли, а названы в честь Фридриха Бесселя.
Содержание
Применения
Уравнение Бесселя возникает во время нахождения решений уравнения Лапласа и уравнения Гельмгольца в цилиндрических и сферических координатах. Поэтому функции Бесселя применяются при решении многих задач о распространении волн, статических потенциалах и т. п., например:
- электромагнитные волны в цилиндрическом волноводе;
- теплопроводность в цилиндрических объектах;
- формы колебания тонкой круглой мембраны
- распределение интенсивности света, дифрагированного на круглом отверстии.
- скорость частиц в цилиндре, заполненном жидкостью и вращающемся вокруг своей оси.
- волновые функции в сферически симметричном потенциальном ящике.
Функции Бесселя применяются и в решении других задач, например, при обработке сигналов.
Определения
Поскольку приведённое уравнение является дифференциальным уравнением второго порядка, у него должно быть два линейно независимых решения. Однако в зависимости от обстоятельств выбираются разные определения этих решений. Ниже приведены некоторые из них.
Функции Бесселя первого рода
Функциями Бесселя первого рода, обозначаемыми
 , являются решения, конечные в точке
, являются решения, конечные в точке  при целых или неотрицательных
при целых или неотрицательных  . Выбор конкретной функции и её нормализации определяются её свойствами. Можно определить эти функции с помощью разложения в ряд Тейлора около нуля (или в более общий степенной ряд при нецелых
. Выбор конкретной функции и её нормализации определяются её свойствами. Можно определить эти функции с помощью разложения в ряд Тейлора около нуля (или в более общий степенной ряд при нецелых  ):
):Здесь
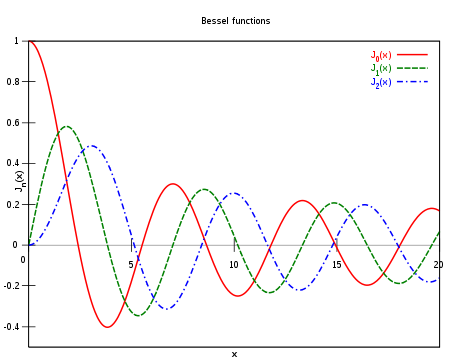
 — это гамма-функция Эйлера, обобщение факториала на нецелые значения. График функции Бесселя похож на синусоиду, колебания которой затухают пропорционально
— это гамма-функция Эйлера, обобщение факториала на нецелые значения. График функции Бесселя похож на синусоиду, колебания которой затухают пропорционально  , хотя на самом деле нули функции расположены не периодично.
, хотя на самом деле нули функции расположены не периодично.Ниже приведены графики
 для
для  :
:Если
 не является целым числом, функции
не является целым числом, функции  и
и  линейно независимы и, следовательно, являются решениями уравнения. Но если
линейно независимы и, следовательно, являются решениями уравнения. Но если  целое, то верно следующее соотношение:
целое, то верно следующее соотношение:Оно означает, что в этом случае функции линейно зависимы. Тогда вторым решением уравнения станет функция Бесселя второго рода (см. ниже).
Интегралы Бесселя
Можно дать другое определение функции Бесселя для целых значений
 , используя интегральное представление:
, используя интегральное представление:Этот подход использовал Бессель, изучив с его помощью некоторые свойства функций. Возможно и другое интегральное представление:
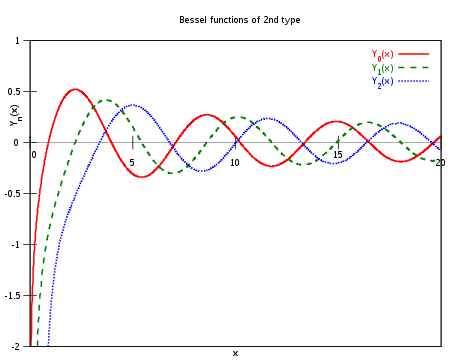
Функции Неймана
Функции Неймана — решения
 уравнения Бесселя, бесконечные в точке
уравнения Бесселя, бесконечные в точке  .
.Эта функция связана с
 следующим соотношением:
следующим соотношением:где в случае целого
 берётся предел по
берётся предел по  , вычисляемый, например, с помощью правила Лопиталя.
, вычисляемый, например, с помощью правила Лопиталя.Функции Неймана также называются функциями Бесселя второго рода. Линейная комбинация функций Бесселя первого и второго родов являет собой полное решение уравнения Бесселя:
Ниже приведён график
 для
для  :
:Свойства
Асимптотика
Для функций Бесселя первого и второго рода известны асимптотические формулы. При малых аргументах
 и неотрицательных
и неотрицательных  они выглядят так:[1]
они выглядят так:[1]![Y_\alpha(x) \rightarrow \left\{ \begin{matrix}
\frac{2}{\pi} \left[ \ln (x/2) + \gamma \right] & \mbox{;}\quad\alpha=0 \\ \\
-\frac{\Gamma(\alpha)}{\pi} \left( \frac{2}{x} \right) ^\alpha & \mbox{;}\quad\alpha > 0
\end{matrix} \right.](74ac42dafbdc57dbfe5e5e9999c2d4d2.png) ,
,
где
 — постоянная Эйлера — Маскерони (0.5772…), а
— постоянная Эйлера — Маскерони (0.5772…), а  — гамма-функция Эйлера. Для больших аргументов (
— гамма-функция Эйлера. Для больших аргументов ( ) формулы выглядят так:
) формулы выглядят так:Гипергеометрический ряд
Функции Бесселя могут быть выражены через гипергеометрическую функцию:
Таким образом, при целых
 функция Бесселя однозначная аналитическая, а при нецелых — многозначная аналитическая.
функция Бесселя однозначная аналитическая, а при нецелых — многозначная аналитическая.Производящая функция
Существует представление для функций Бесселя первого рода и целого порядка через коэффициенты ряда Лорана функции определённого вида, а именно
Соотношения
Формула Якоби — Аигера и связанные с ней
Получается выражения для производящей при
 ,
,  :[2]
:[2]При
 ,
,  :[2]
:[2]Теорема сложения
Для любого целого n и комплексных
 ,
,  выполняется[3]
выполняется[3]Интегральные выражения
Для любых
 и
и  (в том числе комплексных) выполняется[3]
(в том числе комплексных) выполняется[3]Частным случаем последней формулы является выражение
См. также
Примечания
- ↑ Arfken, George B. and Hans J. Weber Mathematical Methods for Physicists. — 6th edition. — San Diego: Harcourt, 2005. — ISBN 0-12-059876-0
- ↑ 1 2 Бейтмен, Эрдейи, 1974, с. 15
- ↑ 1 2 Лаврентьев, Шабат, 1974, с. 15
Литература
- Ватсон Г. Теория бесселевых функций. — М.: ИЛ, 1949. — Т. 1, 2.
- Бейтмен Г., Эрдейи А. Функции Бесселя, функции параболического цилиндра, ортогональные многочлены // Высшие трансцендентные функции = Higher Transcendental Functions / Пер. с англ. Н. Я. Виленкина. — 2-е. — м.: Наука, 1974. — Т. 2. — 296 с.
- Лаврентьев М. А., Шабат Б. В. Методы теории функций комплексного переменного. — 4-е.
Категория:- Цилиндрические функции
Wikimedia Foundation. 2010.