- Серебряное сечение
-
Иррациональные числа
γ - ζ(3) — √2 — √3 — √5 — φ — α — e — π — δСеребряное сечение — это математическая константа, выражающая некоторое геометрическое соотношение, выделяемое эстетически. В отличие от золотого сечения, по аллюзии с которым оно названо, серебряное сечение не имеет единого определения.
Описание вещественного числа Двоичная система счисления 10.0110101000001001111… Десятичная система счисления 2.4142135623730950488… Шестнадцатеричная система счисления 2.6A09E667F3BCC908B2F… Непрерывная дробь 
Наиболее последовательным определением является следующее:
две величины находятся в «серебряном сечении», если отношение суммы меньшей и удвоенной большей величины к большей то же самое, что и отношение большей величины к меньшей. Серебряное сечение — иррациональное, но алгебраическое, число, равное приблизительно 2,4142135623 или точно
 .
.
По крайней мере в последнее время, некоторые художники и архитекторы считают это отношение «красивым». Возможно, они опираются на теорию динамических прямоугольников (англ.) Джея Хембриджа (англ.). Математики исследовали серебряное отношение со времён древнегреческой науки (хотя такое название, возможно, появилось только недавно), так как оно связано с квадратным корнем из 2, его подходящими дробями, квадратными треугольными числами (англ.), числами Пелля, восьмиугольником и др.Обозначим далее серебряное сечение за
 (общепринятого обозначения нет). Соотношение, описанное в определении выше, записывается алгебраически так:
(общепринятого обозначения нет). Соотношение, описанное в определении выше, записывается алгебраически так:Это уравнение имеет единственный положительный корень.
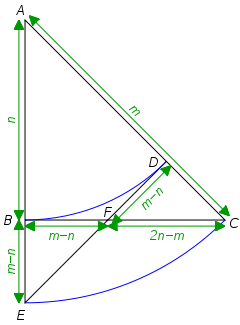
Доказательство:
На рисунке справа даётся геометрическое доказательство, что корень из двух — иррационален, при этом отношения
 .
.Содержание
Формулы
 . Это следует из
. Это следует из 
![\delta_S = [2; 2, 2, 2, \dots]](ea5761622eb8c4ea2c552cdf46dc0577.png) — в виде цепной дроби:
— в виде цепной дроби:
подходящие дроби этой непрерывной дроби (2/1, 5/2, 12/5, 29/12, 70/29, …) являются отношениям последовательных чисел Пелля. Эти дроби дают хорошие рациональные аппроксимации (англ.) серебряного сечения, аналогично тому, что золотое сечение приближается отношениями последовательных чисел Фибоначчи.
Другие определения
Встречаются и другие определения серебряного сечения.
Например, отталкиваясь от определения золотого сечения через цепную дробь, серебряными называют любые цепные дроби, в которых знаменатели постоянны:
![[n; n, n, n, \dots]](c8171d5c17678a7b1b26e179374079dd.png) .
.
Для использования в процентном делении используется отношение, близкое к одной из вышеуказанных подходящих дробей, — 71/29 (в сумме дают 100).
Также встречается определение серебряного сечения: отношение целого отрезка к меньшему как длины окружности к ее диаметру, то есть пи. Особенно этим увлекается поэт, писатель и исследователь старины Андрей Чернов (см. библиографию).
Так, он предполагает, что именно в серебряном сечении разбиваются части некоторых литературных произведений: Медный всадник" А. С. Пушкина и «Слово о полку Игореве». Также в отношении размаха рук человека к его росту Чернов видит число
 , где Φ — число Фидия.
, где Φ — число Фидия.Литература
- Жуков А.В. Такое разное π // Вездесущее число π. — М.: УРСС, 2004. — С. 195-196. — 214 с. — ISBN 5-354-00327-X
- Чернов А. «Серебряное сечение» / Новая газета. — 13.01.1997. — № 2(422). — С. 8-9
- Чернов А. Ю. Семь раз отмерь // Хроники изнаночного времени. — СПб., 2006.
- А. Ф. Черняев Русская матрица - основа золотых пропорций // Золото древней Руси.
- Андрей Чернов. Заметки о вечном. «СЕРЕБРЯНОЕ СЕЧЕНИЕ (введение в проблему)»
Ссылки
- Explanation of Silver Means
- Weisstein, Eric W. Серебряное сечение (англ.) на сайте Wolfram MathWorld.
- Числа Пелля
- Пластическое число
- Золотое сечение
Числа с собственными именами Вещественные Пи • Золотое сечение • Серебряное сечение • e (число Эйлера) • Постоянная Эйлера — Маскерони • Постоянные Фейгенбаума • Постоянная Гельфонда • Константа Бруна • Постоянная Каталана • Постоянная Апери Натуральные Чёртова дюжина • Число зверя • Число Рамануджана — Харди • Число Грэма • Число Скьюза • Число Мозера Степени десяти Мириада • Гугол • Асанкхейя • Гуголплекс Степени тысячи Тысяча • Миллион • Миллиард • Биллион • Триллион • Квадриллион • … • Центиллион Степени двенадцати Дюжина • Гросс • Масса Категории:- Числа с собственными именами
- Математические константы
- Алгебраические числа
Wikimedia Foundation. 2010.








 (последовательность
(последовательность 