- Квадратный корень из 3
-
Иррациональные числа
γ - ζ(3) — √2 — √3 — √5 — φ — α — e — π — δСистема счисления Оценка числа √3 Двоичная 1.1011101101100111101… Десятичная 1.7320508075688772935… Шестнадцатеричная 1.BB67AE8584CAA73B… Непрерывная дробь 
Квадратный корень из числа 3 — положительное действительное число, которое при умножении само на себя даёт число 3.
Его приблизительным значением с 69 цифрами после запятой является:
Округленное значение 1.732 является правильным с точностью до 0,01 %. Приблизительной правильной дробью является
 (1,7321 42857…).
(1,7321 42857…).Квадратный корень из 3 является иррациональным числом. Также известен как Феодоровская постоянная, названная в честь Феодора Киренского.
Может быть выражен в виде непрерывной дроби [1; 1, 2, 1, 2, 1, 2, …].
Содержание
Геометрия
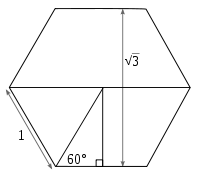
Если равносторонний треугольник со сторонами длиной 1 делится на две равные половины, пересечением внутреннего угла для составления прямого угла с одной стороной, то получившийся прямоугольный треугольник имеет гипотенузу со стороной 1 и катеты длиной 1/2 и
 Поэтому тангенс 60° равен
Поэтому тангенс 60° равен 
Так же, это расстояние между параллельными сторонами правильного шестиугольника со сторонами 1.
 является длиной диагонали куба со стороной 1.
является длиной диагонали куба со стороной 1.Использование в других областях
Энергетика
При трехфазной системе токов модуль напряжения между двумя фазами (линейное напряжение) в
 больше модуля фазного напряжения
больше модуля фазного напряженияСм. также
Ссылки
Категории:- Алгебраические числа
- Математические константы
- Иррациональные числа
Wikimedia Foundation. 2010.