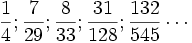- Подходящая дробь
-
Цепная дробь (или непрерывная дробь) — это математическое выражение вида
где a0 есть целое число и все остальные an натуральные числа (то есть положительные целые). Любое вещественное число можно представить в виде цепной дроби (конечной или бесконечной). Число представляется конечной цепной дробью тогда и только тогда, когда оно рационально. Число представляется периодической цепной дробью тогда и только тогда, когда оно является квадратичной иррациональностью.
Содержание
Разложение в цепную дробь
Любое вещественное число x может быть представлено (конечной или бесконечной) цепной дробью
![[a_0; a_1, a_2, a_3,\cdots]](/pictures/wiki/files/48/01f9a60e25d53a9ede7edb78bfe4279d.png) , где
, гдегде
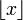 обозначает целую часть числа x.
обозначает целую часть числа x.Для рационального числа x это разложение оборвётся по достижению нулевого xn для некоторого n. В этом случае x представляется конечной цепной дробью
![x = [a_0; a_1, \cdots, a_n]](/pictures/wiki/files/99/c8bb5d7e87432f4d3193b81c1071d50c.png) .
.Для иррационального x все величины xn будут ненулевыми и процесс разложения можно продолжать бесконечно. В этом случае x представляется бесконечной цепной дробью
![x = [a_0; a_1, a_2, a_3,\cdots]](/pictures/wiki/files/54/6fd54fa6fbc33be32f6151e4945b3472.png) .
.Подходящие дроби
n-ой подходящей дробью для цепной дроби
![x=[a_0; a_1, a_2, a_3,\cdots]](/pictures/wiki/files/54/6fd54fa6fbc33be32f6151e4945b3472.png) , называется конечная цепная дробь
, называется конечная цепная дробь ![[a_0; a_1, \cdots, a_n]](/pictures/wiki/files/51/3494a98cf282eaa3cd3aa63744333d83.png) , значение которой равно некоторому рациональному числу
, значение которой равно некоторому рациональному числу 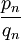 . Подходящие дроби с чётными номерами образуют возрастающую последовательность, предел которой равен x. Аналогично, подходящие дроби с нечётными номерами образуют убывающую последовательность, предел которой также равен x.
. Подходящие дроби с чётными номерами образуют возрастающую последовательность, предел которой равен x. Аналогично, подходящие дроби с нечётными номерами образуют убывающую последовательность, предел которой также равен x.Эйлер вывел рекуррентные формулы для вычисления числителей и знаменателей подходящих дробей:
Таким образом, величины pn и qn представляются значениями континуант:
Последовательности
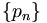 и
и 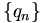 являются возрастающими.
являются возрастающими.Числители и знаменатели соседних подходящих дробей связаны соотношением:
pnqn - 1 - qnpn - 1 = ( - 1)n - 1, (1) которое можно переписать в виде
Откуда следует, что
Приближение вещественных чисел рациональными
Цепные дроби позволяют эффективно находить хорошие рациональные приближения вещественных чисел. А именно, если вещественное число x разложить в цепную дробь, то её подходящие дроби будут удовлетворять неравенству
Отсюда, в частности, следует:
- подходящая дробь
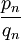 является наилучшим приближением для x среди всех дробей, знаменатель которых не превосходит qn;
является наилучшим приближением для x среди всех дробей, знаменатель которых не превосходит qn; - мера иррациональности любого иррационального числа не меньше 2.
Примеры
- Разложим число π=3,14159265… в непрерывную дробь и подсчитаем его подходящие дроби:
- 3, 22/7, 333/106, 355/113, 103993/33102, …
- Вторая дробь (22/7) — это известное архимедово приближение. Четвёртая (355/113) была впервые получена в Древнем Китае.
- В теории музыки требуется отыскать рациональное приближение для
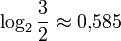 . Третья подходящая дробь: 7/12 соответствует классической октаве из 12 полутонов.[1]
. Третья подходящая дробь: 7/12 соответствует классической октаве из 12 полутонов.[1]
Свойства и примеры
- Любое рациональное число может быть представлено в виде конечной цепной дроби двумя способами, например:
- Теорема Лагранжа: Число представляется в виде бесконечной периодической цепной дроби тогда и только тогда, когда оно является иррациональным решением квадратного уравнения с целыми коэффициентами.
- Например:
- Для остальных — не квадратичных — алгебраических чисел характер разложений совершенно не известен. До сих пор неизвестно разложение хотя бы одного алгебраического числа степени N>2 в цепную дробь.
- Для некоторых трансцендентных чисел можно найти простую закономерность. Например, для основания натурального логарифма:
-
- e − 1 = [1;1;2;1;1;4;1;1;6;1;1;8;...;1;1;2n − 2;1;1;2n;...]
для числа
-
- tg1 = [1;1;1;3;1;5;1;7;...;1;2n + 1;1;2n + 3;...]
- Для числа пи подобной закономерности не выявлено:
-
- π = [3; 7, 15, 1, 292, 1, 1, 1, 2, 1, 3, 1, 14, 2, 1, 1, 2, 2, 2, 2, 1, 84, 2, 1, 1, 15,…]
- Теорема Гаусса — Кузмина: Почти для всех (кроме множества меры нуль) действительных чисел существует среднее геометрическое коэффициентов соответствующих им цепных дробей, и оно равно одному и тому же числу.
Приложения цепных дробей
Теория календаря
При разработке солнечного календаря необходимо найти приближение для числа дней в году, которое равно 365,2421988… Подсчитаем подходящие дроби для этого числа:
Первая дробь означает, что раз в 4 года надо добавлять лишний день; этот принцип лёг в основу юлианского календаря. При этом ошибка в 1 день накапливается за 128 лет. Второе значение (7/29) никогда не использовалось. Третья дробь (8/33), то есть 8 високосных лет за период в 33 года, была предложена Омаром Хайямом в XI веке и положила начало персидскому календарю, в котором ошибка в день накапливается за 4500 лет. Вариант 31/128 пропагандировал немецкий астроном Медлер (1864), однако большого интереса он не вызвал, так как существенных преимуществ перед григорианским не имел.
Решение сравнений первой степени
Рассмотрим сравнение:
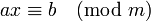 , где
, где 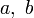 известны, причём можно считать, что a взаимно просто с m. Надо найти x.
известны, причём можно считать, что a взаимно просто с m. Надо найти x.Разложим
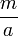 в непрерывную дробь. Она будет конечной, и последняя подходящая дробь
в непрерывную дробь. Она будет конечной, и последняя подходящая дробь 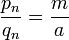 . Подставим в формулу (1):
. Подставим в формулу (1):- mqn − 1 − apn − 1 = ( − 1)n − 1
Отсюда вытекает:
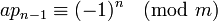 , или:
, или: 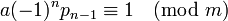
Вывод: класс вычетов
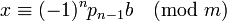 является решением исходного сравнения.
является решением исходного сравнения.Другие приложения
- Доказательство иррациональности чисел. Например, с помощью цепных дробей была доказана иррациональность значения дзета-функции Римана ζ(3)
- Определение заведомо трансцендентного числа (см. теорема Лиувилля)
- Алгоритмы факторизации SQUFOF и CFRAC.
- Характеристика ортогональных многочленов
- Характеристика стабильных многочленов
Историческая справка
Античные математики умели представлять отношения несоизмеримых величин в виде цепочки последовательных подходящих отношений, получая эту цепочку с помощью алгоритма Евклида. По-видимому, именно таким путём Архимед получил приближение
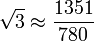 — это 12-я подходящая дробь для
— это 12-я подходящая дробь для 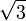 или
или  от 4-й подходящей дроби для
от 4-й подходящей дроби для 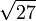 .
.В V веке индийский математик Ариабхата применял аналогичный «метод измельчения» для решения неопределённых уравнений первой и второй степени. С помощью этой же техники было, вероятно, получено известное приближение для числа π (355/113). В XVI веке Рафаэль Бомбелли извлекал с помощью цепных дробей квадратные корни (см. его алгоритм).
Начало современной теории цепных дробей положил в 1613 году Пьетро Антонио Катальди. Он отметил основное их свойство (положение между подходящими дробями) и ввёл обозначение, напоминающее современное. Позднее его теорию расширил Джон Валлис, который и предложил термин «непрерывная дробь». Эквивалентный термин «цепная дробь» появился в конце XVIII века.
Применялись эти дроби в первую очередь для рационального приближения вещественных чисел; например, Христиан Гюйгенс использовал их для проектирования зубчатых колёс своего планетария. Гюйгенс уже знал, что подходящие дроби всегда несократимы и что они представляют наилучшее рациональное приближение.
В XVIII веке теорию цепных дробей в общих чертах завершили Леонард Эйлер и Жозеф Луи Лагранж.
См. также
Ссылки
- В. И. Арнольд Цепные дроби. — М.: МЦНМО, 2000. — Т. 14. — 40 с. — (Библиотека «Математическое просвещение»).
- Н. М. Бескин Цепные дроби // Квант. — 1970. — Т. 1. — С. 16—26,62.
- Н. М. Бескин Бесконечные цепные дроби // Квант. — 1970. — Т. 8. — С. 10—20.
- А. А. Бухштаб Теория чисел. — М.: Просвещение, 1966. — 384 с.
- И. М. Виноградов Основы теории чисел. — М.-Л.: Гос. изд. технико-теоретической литературы, 1952. — 180 с.
- С. Н. Гладковский Анализ условно-периодических цепных дробей, ч. 1. — Незлобная: 2009. — 138 с.
- И. Я. Депман История арифметики. Пособие для учителей. — Изд.второе. — М.: Просвещение, 1965. — С. 253—254.
- Г. Дэвенпорт Высшая Арифметика. — М.: Наука, 1965.
- С. В. Сизый Лекции по теории чисел. — Екатеринбург: Уральский государственный университет им. А. М. Горького, 1999.
- А. Я. Хинчин Цепные дроби. — М.: ГИФМЛ, 1960.
Примечания
- ↑ См. Шилов Г. Е. Простая гамма. Устройство музыкальной шкалы. М.: Физматгиз, 1963. 20 с. Серия «Популярные лекции по математике», выпуск 37.
Wikimedia Foundation. 2010.

![[a_0; a_1, a_2, a_3,\cdots] = a_0+\cfrac{1}{a_1+\cfrac{1}{a_2+\cfrac{1}{a_3+\ldots}}}\;](/pictures/wiki/files/56/8fe9c011be1bbb9688becb134bef0b85.png)
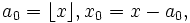
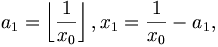
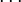
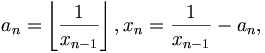
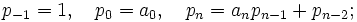
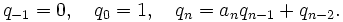
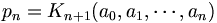
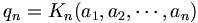
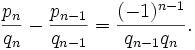
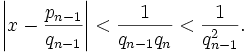
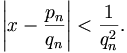
![9/4=[2; 3, 1] = [2; 4]\;](/pictures/wiki/files/56/8e8b27eed5b9a2f8a16131f15b3413b9.png)
![\sqrt{2} = [1; 2, 2, 2, 2, \dots]](/pictures/wiki/files/100/d046b2d51bf8be221d9c8a619064e40e.png)
![\phi = [1;1,1,1,\dots]](/pictures/wiki/files/51/3431f54201687dc2e8c8450d75b440ce.png)