Квадратный корень из 5

Иррациональные числа γ - ζ(3) — √2 — √3 — √5 — φ — α — e — π — δ
Система счисления	Оценка числа √5
Двоичная	10.0011110001101111…
Десятичная	2.23606797749978969…
Шестнадцатеричная	2.3C6EF372FE94F82C…
Непрерывная дробь	$2 + \cfrac{1}{4 + \cfrac{1}{4 + \cfrac{1}{4 + \cfrac{1}{4 + \ddots}}}}$

Квадратный корень из числа 5 — положительное действительное число, которое при умножении само на себя даёт число 5. Это иррациональное и алгебраическое число.^[1]

Его приблизительное значение с 59 цифрами после запятой является:

$\sqrt{5}=2{,}236\;067\;977\;499\;789\;696\;409\;173\;668\;731\;276\;235\;440\;618\;359\;611\;525\;724\;270\;89\ldots$

Округлённое значение 2.236 является правильным с точностью до 0,01 %. Компьютерная вычисленная точность составляет не менее 1 000 000 знаков.^[2]

Может быть выражено в виде непрерывной дроби [2; 4, 4, 4, 4, 4, 4, …], последовательно это дроби:

${\color{OliveGreen}\frac{2}{1}}, \frac{7}{3} , {\color{OliveGreen}\frac{9}{4}} , \frac{20}{9} , \frac{29}{13} , {\color{OliveGreen}\frac{38}{17}} , \frac{123}{55} , {\color{OliveGreen}\frac{161}{72}} , \frac{360}{161} , \frac{521}{233} , {\color{OliveGreen}\frac{682}{305}} , \frac{2207}{987} , {\color{OliveGreen}\frac{2889}{1292}}, \dots$

Вавилонский метод

Вычисление корня из 5, начиная с r₀ = 2, где r_n+1 = (r_n + 5/r_n) / 2:

$\frac{2}{1} = 2.0,\quad \frac{9}{4} = 2.25,\quad \frac{161}{72} = 2.23611\dots,\quad \frac{51841}{23184} = 2.2360679779 \ldots$

Золотое сечение

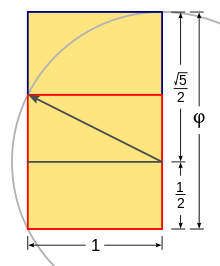√5/2 — диагональ половины квадрата, представляет собой геометрическое представление о золотом сечении.

Золотое сечение φ — среднее арифметическое 1 и корня из 5.^[3]

($\Phi = 1 / \varphi = \varphi^{-1}$) алгебраически можно выразить так:

$\sqrt{5} = \varphi + \Phi = 2\varphi - 1 = 2\Phi + 1$

$\varphi = \frac{\sqrt{5} + 1}{2}$

$\Phi = \frac{\sqrt{5} - 1}{2}.$

Числа Фибоначчи могут быть выражены через корень из 5 так:

$F\left(n\right) = {{\varphi^n-(1-\varphi)^n} \over {\sqrt 5}}.$

Отношение √5 к φ и наоборот дают интересные зависимости непрерывных дробей с числами Фибоначчи и числами Люка:^[4]

$\frac{\sqrt{5}}{\varphi} = \Phi \cdot \sqrt{5} = \frac{5 - \sqrt{5}}{2} = 1.3819660112501051518\dots = [1; 2, 1, 1, 1, 1, 1, 1, 1, \dots]$

$\frac{\varphi}{\sqrt{5}} = \frac{1}{\Phi \cdot \sqrt{5}} = \frac{5 + \sqrt{5}}{10} = 0.72360679774997896964\dots = [0; 1, 2, 1, 1, 1, 1, 1, 1, \dots].$

${1, \frac{3}{2}, \frac{4}{3}, \frac{7}{5}, \frac{11}{8}, \frac{18}{13}, \frac{29}{21}, \frac{47}{34}, \frac{76}{55}, \frac{123}{89}}, \dots \dots [1; 2, 1, 1, 1, 1, 1, 1, 1, \dots]$

${1, \frac{2}{3}, \frac{3}{4}, \frac{5}{7}, \frac{8}{11}, \frac{13}{18}, \frac{21}{29}, \frac{34}{47}, \frac{55}{76}, \frac{89}{123}}, \dots \dots [0; 1, 2, 1, 1, 1, 1, 1, 1,\dots].$

Алгебра

Кольцо $\scriptstyle\mathbb{Z}\left[\,\sqrt{-5}\,\right]$ содержит числа вида $\scriptstyle a\, +\, b\sqrt{-5}$, где a и b целые числа и $\scriptstyle \sqrt{-5}$ мнимое число $\scriptstyle i\sqrt{5}$. Это кольцо является примером области целостности, не являющейся факториальным кольцом.

Число 6 представляется в данном кольце двумя способами:

$6 = 2 \cdot 3 = (1 - \sqrt{-5})(1 + \sqrt{-5}). \,$

Поле $\scriptstyle\mathbb{Q}\left[\,\sqrt{5}\,\right]$ — абелево расширение рациональных чисел.

Теорема Кронекера — Вебера утверждает, что корень из 5 можно выразить линейной комбинацией корней из единицы:

$\sqrt5 = e^{2\pi i/5} - e^{4\pi i/5} - e^{6\pi i/5} + e^{8\pi i/5}. \,$

Тождества Рамануджана

Корень из 5 появляется во множестве тождеств Рамануджана с непрерывными дробями.^[5][6]

Например, случай непрерывных дробей Роджерса-Рамануджана:

$\cfrac{1}{1 + \cfrac{e^{-2\pi}}{1 + \cfrac{e^{-4\pi}}{1 + \cfrac{e^{-6\pi}}{1 + \ddots}}}} = \left( \sqrt{\frac{5 + \sqrt{5}}{2}} - \frac{\sqrt{5} + 1}{2} \right)e^{2\pi/5} = e^{2\pi/5}\left( \sqrt{\varphi\sqrt{5}} - \varphi \right).$

$\cfrac{1}{1 + \cfrac{e^{-2\pi\sqrt{5}}}{1 + \cfrac{e^{-4\pi\sqrt{5}}}{1 + \cfrac{e^{-6\pi\sqrt{5}}}{1 + \ddots}}}} = \left( {\sqrt{5} \over 1 + \left[5^{3/4}(\varphi - 1)^{5/2} - 1\right]^{1/5}} - \varphi \right)e^{2\pi/\sqrt{5}}.$

$4\int_0^\infty\frac{xe^{-x\sqrt{5}}}{\cosh x}\,dx = \cfrac{1}{1 + \cfrac{1^2}{1 + \cfrac{1^2}{1 + \cfrac{2^2}{1 + \cfrac{2^2}{1 + \cfrac{3^2}{1 + \cfrac{3^2}{1 + \ddots}}}}}}}.$

См. также

• Квадратный корень из 2
• Квадратный корень из 3

Примечания

1. ↑ Dauben, Joseph W. (June 1983) Scientific American Georg Cantor and the origins of transfinite set theory. Volume 248; Page 122.
2. ↑ R. Nemiroff and J. Bonnell: The first 1 million digits of the square root of 5
3. ↑ Browne, Malcolm W. (July 30, 1985) New York Times Puzzling Crystals Plunge Scientists into Uncertainty. Section: C; Page 1. (Note — this is a widely cited article).
4. ↑ Richard K. Guy: «The Strong Law of Small Numbers». American Mathematical Monthly, vol. 95, 1988, pp. 675—712
5. ↑ Ramanathan, K. G. (1984), "«On the Rogers-Ramanujan continued fraction»", Indian Academy of Sciences. Proceedings. Mathematical Sciences Т. 93 (2): 67-77, MR813071, ISSN 0253-4142, DOI 10.1007/BF02840651 
6. ↑ Eric W. Weisstein, «Ramanujan Continued Fractions», <http://mathworld.wolfram.com/RamanujanContinuedFractions.html>  at MathWorld

Ссылки

• Proof that square root of 3 is irrational  (англ.)
• Theodorus' Constant at MathWorld