- Свёртка функций
-
Свёртка фу́нкций в функциональном анализе — это операция, показывающая «схожесть» одной функции с отражённой и сдвинутой копией другой. Понятие свёртки обобщается для функций, определённых на группах, а также мер.
Содержание
Свёртка функций
Пусть
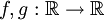 — две функции вещественной переменной, интегрируемые относительно меры Лебега. Тогда их свёрткой называется функция
— две функции вещественной переменной, интегрируемые относительно меры Лебега. Тогда их свёрткой называется функция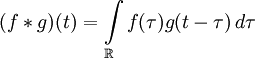 .
.
Свойства
- f * g = g * f.
- f * (g * h) = (f * g) * h.
- f * (g + h) = (f * g) + (f * h);
- Ассоциативность умножения на скаляр:
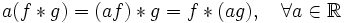 .
.
- Правило дифференцирования:
- D(f * g) = Df * g = f * Dg,
где Df обозначает производную функции f.
- Свойство Фурье-образа:
![\mathcal{F}[f * g] = \mathcal{F} [f] \cdot \mathcal{F} [g]](/pictures/wiki/files/55/7f9360ba05ad88b9502ec1e5b12f76df.png) ,
,
где
![\mathcal{F}[f]](/pictures/wiki/files/55/74d8d9cf1fef828b858860c72324814c.png) обозначает преобразование Фурье функции f.
обозначает преобразование Фурье функции f.Свёртка на группах
Пусть G — группа Ли, оснащённая мерой Хаара m, и
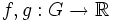 — две функции, определённые на G. Тогда их свёрткой называется функция
— две функции, определённые на G. Тогда их свёрткой называется функция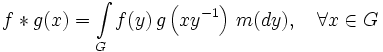 .
.
Свёртка мер
Пусть есть борелевское пространство
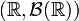 и две меры
и две меры 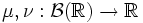 . Тогда их свёрткой называется мера
. Тогда их свёрткой называется мера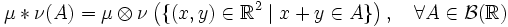 ,
,
где
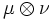 обозначает произведение мер μ и ν.
обозначает произведение мер μ и ν.Свойства
- Пусть μ,ν абсолютно непрерывны относительно меры Лебега m. Обозначим их производные Радона — Никодима:
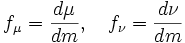 .
.
Тогда μ * ν также абсолютно непрерывна относительно m, и её производная Радона — Никодима
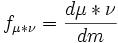 имеет вид
имеет вид- fμ * ν = fμ * fν.
- Если μ,ν — вероятностные меры, то μ * ν также является вероятностной мерой.
Свёртка распределений
Если
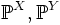 — распределения двух независимых случайных величин X и Y, то
— распределения двух независимых случайных величин X и Y, то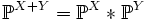 ,
,
где
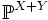 — распределение суммы X + Y. В частности, если X,Y абсолютно непрерывны и имеют плотности fX,fY, то случайная величина X + Y также абсолютно непрерывна и её плотность имеет вид:
— распределение суммы X + Y. В частности, если X,Y абсолютно непрерывны и имеют плотности fX,fY, то случайная величина X + Y также абсолютно непрерывна и её плотность имеет вид:- fX + Y = fX * fY.
Ссылки
Wikimedia Foundation. 2010.
