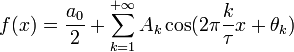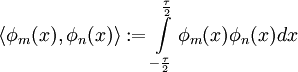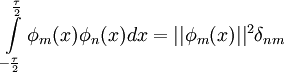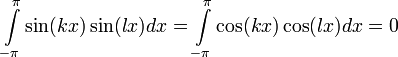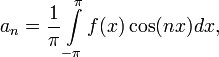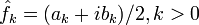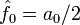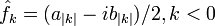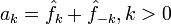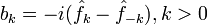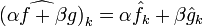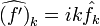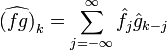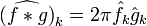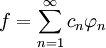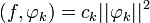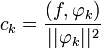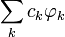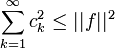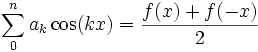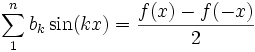Ряды Фурье

Ряд Фурье — представление произвольной функции f с периодом τ в виде ряда

$f(x) = \frac{a_0}{2} + \sum\limits_{k=1}^{+\infty} A_k\cos(2\pi \frac{k}{\tau}x+\theta_k)$

Этот ряд может быть также переписан в виде

$f(x) = \sum\limits_{k=-\infty}^{+\infty} \hat{f}_k e^{i2\pi \frac{k}{\tau}x}$.

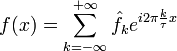где

A_k — амплитуда k-го гармонического колебания (функции cos),

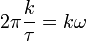$2\pi \frac{k}{\tau} = k\omega$ — круговая частота гармонического колебания,

θ_k - начальная фаза k-го колебания,

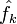$\hat{f}_k$ - k-я комплексная амплитуда

В более общем виде рядом Фурье элемента гильбертова пространства называется разложение этого элемента по ортогональному базису. Существует множество систем ортогональных функций: Уолша, Лагера, Котельникова...

Разложение функции в ряд Фурье является мощным инструментом при решении самых разных задач благодаря тому, что ряд Фурье прозрачным образом ведёт себя при дифференцировании, интегрировании, сдвиге функции по аргументу и свёртке функций.

Тригонометрический ряд Фурье

Неформальное обсуждение

Вектор в евклидовом пространстве можно разложить по ортонормированному базису. При этом многие действия с этим вектором станут намного проще. Функции, заданные на некотором замкнутом ограниченном промежутке, во многом аналогичны векторам — они также образуют линейное пространство, их можно складывать и умножать на числа. Не можем ли мы определить и в этом случае аналогичную процедуру разложения по базису?

Ответ: можем. Для этого необходимо определить наше пространство функций, задать на этом пространстве скалярное произведение и зафиксировать базис, по которому мы будем раскладывать. Наиболее удобные и естественные (для большинства случаев) определение скалярного произведения и выбор базиса приводят к тригонометрическому ряду Фурье.

Скалярное произведение и ортогональность

Пусть φ_n, φ_m — две функции пространства $L^2[-\frac{\tau}{2},\frac{\tau}{2}]$. Определим их скалярное произведение

$\langle \phi_m(x), \phi_n(x)\rangle:=\int\limits_{-\frac{\tau}{2}}^{\frac{\tau}{2}}\phi_m(x)\phi_n(x)dx$

Условие ортогональности

$\int\limits_{-\frac{\tau}{2}}^{\frac{\tau}{2}}\phi_m(x)\phi_n(x)dx = ||\phi_m(x)||^2\delta_{nm}$

где δ_nm - дельта Кронекера. Таким образом, скалярное произведение ортогональных функций равно квадрату нормы функции при n = m или нулю в противном случае.

Следующее наблюдение является ключевым в теории рядов Фурье: функции вида sin(kx), cos(kx) попарно ортогональны относительно этого скалярного произведения, то есть при всех целых неотрицательных $k\neq l$:

$\int\limits_{-\pi}^{\pi}\sin(kx)\sin(lx)dx = \int\limits_{-\pi}^{\pi}\cos(kx)\cos(lx)dx = 0$

и при всех целых неотрицательных k, l

$\int\limits_{-\pi}^{\pi}\cos(kx)\sin(lx)dx = 0$.

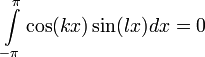Еще одно важное свойство состоит в том, что тригонометрическая система функций является базисом в пространстве L²[0,2π]. Иными словами, если некоторая функция из этого пространства ортогональна всем функциям вида 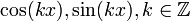$\cos(kx), \sin(kx), k\in\mathbb{Z}$, то она тождественно равна нулю (если точнее, то равна нулю почти всюду).

Классическое определение

Тригонометрическим рядом Фурье функции $f\in L_2([-\pi,\pi])$ называют функциональный ряд вида

$f(x)=\frac{a_0}{2} + \sum^{\infin}_{n=1} (a_n \cos nx + b_n \sin nx)$

(1)

где

$a_n= \frac{1}{\pi}\int\limits_{-\pi}^{\pi}f(x)\cos(nx)dx,$

$b_n= \frac{1}{\pi}\int\limits_{-\pi}^{\pi}f(x)\sin(nx)dx,$

Числа a₀, a_n и b_n ($n = 1, 2, \ldots$) называются коэффициентами Фурье функции f. Формулы для них можно объяснить следующим образом. Предположим, мы хотим представить функцию $f\in L_2([0,2\pi])$ в виде ряда (1), и нам надо определить неизвестные коэффициенты a₀, a_n и b_n. Если умножить правую часть (1) на cos(kx) и проинтегрировать по промежутку [ − π,π], благодаря ортогональности в правой части все слагаемые обратятся в нуль, кроме одного. Из полученного равенства легко выражается коэффициент a_k. Аналогично для b_k

Ряд (1) сходится к функции f в пространстве L₂([ − π,π]). Иными словами, если обозначить через S_k(x) частичные суммы ряда (1):

$S_k(x)=\frac{a_0}{2} + \sum^{k}_{n=1} (a_n \cos nx + b_n \sin nx)$,

то их среднеквадратичное отклонение от функции f будет стремиться к нулю:

$\lim\limits_{k\rightarrow \infty}\int\limits_{-\pi}^{\pi}(f(x)-S_k(x))^2dx=0$.

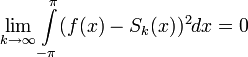Несмотря на среднеквадратичную сходимость, ряд Фурье функции, вообще говоря, не обязан сходиться к ней поточечно(см.ниже).

Комплексная запись

Часто при работе с рядами Фурье бывает удобнее в качестве базиса использовать вместо синусов и косинусов экспоненты мнимого аргумента. Мы рассматриваем пространство $L^2([-\pi,\pi],\mathbb{C})$ комплекснозначных функций со скалярным произведением

$\langle f,g\rangle := \int\limits_{-\pi}^{\pi}f(x)\overline{g(x)}dx$.

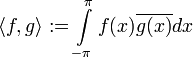Мы также рассматриваем систему функций

$\varphi_k(x)=e^{ikx}=\cos(kx)+i\sin(kx), k\in\mathbb{Z}$.

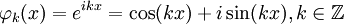Как и прежде, эти функции являются попарно ортогональными и образуют полную систему, и, таким образом, любая функция $f\in L^2([-\pi,\pi],\mathbb{C})$ может быть разложена по ним в ряд Фурье:

$f(x) = \sum\limits_{k=-\infty}^{+\infty} \hat{f}_k e^{ikx}$,

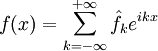где ряд в правой части сходится к f по норме в $f\in L^2([-\pi,\pi],\mathbb{C})$. Здесь

$\hat{f}_k= \frac{1}{2\pi}\int\limits_{-\pi}^{\pi}f(x)e^{-ikx}dx,$.

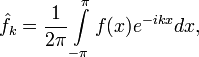Коэффициенты : 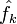$\hat{f}_k$ связаны с классическими коэффициентами Фурье по следующим формулам:

  

$\hat{f}_k = (a_k+ib_k)/2, k>0$

$\hat{f}_0 = a_0/2$

$\hat{f}_k = (a_{|k|}-ib_{|k|})/2, k<0$

$a_k = \hat{f}_k+\hat{f}_{-k}, k>0$

$b_k = -i(\hat{f}_k-\hat{f}_{-k}), k>0$

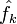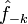• Комплексная функция вещественной переменной раскладывается в такой же ряд Фурье по мнимым экспонентам, как и вещественная, но, в отличие от последней, для ее разложения $\hat{f}_k$ и $\hat{f}_{-k}$ не будут, вообще говоря, комплексно сопряженными.

Свойства тригонометрического ряда Фурье

Все утверждения этого параграфа верны в предположении, что участвующие в них функции (и результаты операций с ними) лежат в пространстве $L^2([-\pi,\pi],\mathbb{C})$.

• Вычисление коэффициентов Фурье является линейной операцией:

$\widehat{(\alpha f+\beta g)}_k=\alpha \hat{f}_k+\beta\hat{g}_k$

• Справедливо равенство Парсеваля:

$2\pi \sum_{k=1}^\infty \hat{|f|}_k^2 = ||f||_2^2$.

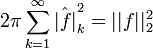• Коэффициенты Фурье производной легко выражаются через коэффициенты Фурье самой функции:

$\widehat{(f')}_k=ik\hat{f}_k$

• коэффициенты Фурье произведения двух функций выражаются сверткой коэффициентов Фурье сомножителей:

$\widehat{(fg)}_k=\sum\limits_{j=-\infty}^{\infty}\hat{f}_j\hat{g}_{k-j}$

• рассмотрим операцию свертки функций:

$(f\ast g)(t):=\int\limits_{-\pi}^{\pi} f(t-x)g(x) dx,$

где функции предполагаются периодически продолженными с промежутка [ − π,π] на всю прямую. Тогда

$\widehat{(f\ast g)}_k =2\pi\hat{f}_k\hat{g}_k$

Обобщения

Ряды Фурье в гильбертовом пространстве

Описанную выше конструкцию можно обобщить со случая пространства L²[ − π,π] с тригонометрической системой на произвольное гильбертово пространство. Пусть даны ортогональная система 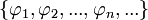$\{\varphi_1, \varphi_2, ..., \varphi_n, ...\}$ в гильбертовом пространстве R и f — произвольный элемент из R. Предположим, мы хотим представить f в виде (бесконечной) линейной комбинации элементов $\{\varphi_k\}$:

$f = \sum^{\infin}_{n=1}c_n\varphi_n$

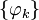Домножим это выражение на 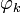$\varphi_k$. С учётом ортогональности системы функций 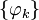$\{\varphi_k\}$ все слагаемые ряда обращаются в ноль, кроме слагаемого при n = k:

$(f, \varphi_k) = c_k||\varphi_k||^2$

Последовательность чисел

$c_k =\frac{(f, \varphi_k)}{||\varphi_k||^2}$

называется координатами, или коэффициентами Фурье элемента f по системе 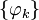$\{\varphi_k\}$, а ряд

$\sum_k c_k \varphi_k$

называется рядом Фурье элемента f по ортогональной системе $\{\varphi_k\}$.

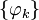Ряд Фурье любого элемента f по любой ортогональной системе сходится в пространстве R, но его сумма не обязательно равна f. Для ортонормированной системы 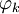${\varphi_k}$ в сепарабельном гильбертовом пространстве следующие условия эквивалентны:

• система является базисом, то есть сумма ряда Фурье любого элемента равна этому элементу.
• система является полной, то есть в R не существует ненулевого элемента, ортогонального всем элементам 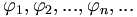$\varphi_1, \varphi_2, ..., \varphi_n, ...$ одновременно.
• система является замкнутой, то есть для любого 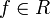$f\in R$ выполнено равенство Парсеваля

$\sum_{k=1}^\infty c_k^2 = ||f||^2$.

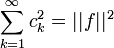• линейные комбинации элементов 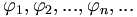$\varphi_1, \varphi_2, ..., \varphi_n, ...$ плотны в пространстве R.

Если эти условия не выполняются, то сумма ряда Фурье элемента f равна его ортогональной проекции на замыкание линейной оболочки элементов 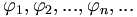$\varphi_1, \varphi_2, ..., \varphi_n, ...$. В этом случае вместо равенства Парсеваля справедливо неравенство Бесселя:

$\sum_{k=1}^\infty c_k^2 \le ||f||^2$

Примеры  

Тригонометрические функции sin(kx), cos(kx) образуют базис гильбертова пространства L₂[ − π,π]. Если мы рассмотрим только косинусы или только синусы, то такая система больше не будет полной. Замыкание линейной обоблочки функций cos(kx) - это все четные функции из L₂, а замыкание линейной оболочки функций sin(kx) - все нечетные функции. Результатом разложения функции f в ряды Фурье по этим системам будут соответственно четная и нечетная части функции f:

$\sum\limits_0^n a_k \cos(kx) = \frac{f(x)+f(-x)}{2}$

$\sum\limits_1^n b_k \sin(kx) = \frac{f(x)-f(-x)}{2}$

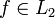Еще более интересная ситуация возникает при рассмотрении системы $\{e^{ikx}\}_{k=0}^{+\infty}$. Эта система вновь не будет полной. Замыкание ее линейной оболочки — пространство Харди H₂. Элементы этого пространства -- те и только те функции $f\in L_2$, что f(t) = g(e^it), где g — граничные значения некоторой функции, аналитической в круге | z | < 1

Двойственность Понтрягина

Основная статья: Двойственность Понтрягина

При обобщении теории рядов Фурье на случай гильбертовых пространств теряются свойства, выражающие связь рядов Фурье со сверткой — то, что коэффициенты Фурье свертки функций являются почленными произведениями их коэффициентов Фурье, и наоборот, коэффициенты Фурье произведения представляются сверткой коэффициентов Фурье сомножителей. Эти свойства являются ключевыми для приложений теории Фурье к решению дифференциальных, интегральных и других функциональных уравнений. Поэтому большой интерес представляет такие обобщения теории рядов Фурье, при которых эти свойства сохраняются. Таким обобщением является теория двойственности Понтрягина. Она рассматривает функции, заданные на локально-компактных абелевых группах. Аналогом ряда Фурье такой функции будет функция, заданная на двойственной группе.

Сходимость ряда Фурье

Сходимость ряда Фурье

Обзор результатов о сходимости ряда Фурье

Обозначим через S_N(f,x) частичные суммы ряда Фурье функции f(x):

$S_N(f,x):=\sum\limits_{k=-N}^N\hat{f}_ke^{ikx}$.

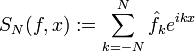Далее обсуждается сходимость последовательности функций S_N(f,x) к функции f(x) в различных смыслах. Функция f предполагается 2π-периодической (если она задана только на промежутке [ − π,π], ее можно периодически продолжить).

• Если $f\in L_2([-\pi,\pi])$, то последовательность S_N(f,x) сходится к функции f(x) в смысле L₂. Кроме того, S_N(f,x) являются наилучшим (в смысле расстояния в L₂) приближением функции f тригонометрическим многочленом степени не выше N.
• Сходимость ряда Фурье в заданной точке x₀ — локальное свойство, то есть, если функции f и g совпадают в некоторой окрестности x₀, то последовательности S_N(f,x₀) и S_N(g,x₀) либо одновременно расходятся, либо одновременно сходятся, и в этом случае их пределы совпадают.
• Если функция f дифференцируема в точке x₀, то ее ряд Фурье в этой точке сходится к f(x₀). Более точные достаточные условия в терминах гладкости функции f задаются признаком Дини.
• Функция, непрерывная в точке x₀, может иметь расходящийся в ней ряд Фурье. Однако, если он сходится, то непременно к f(x₀). Это следует из того, что для непрерывной в x₀ функции f последовательность S_N(f,x₀) сходится по Чезаро к f(x₀).
• Если функция f разрывна в точке x₀, но имеет пределы в этой точке справа и слева $f(x_0+0)\neq f(x_0-0)$, то при некоторых дополнительных условиях S_N(f,x₀) сходятся к (f(x₀ + 0) + f(x₀ − 0)) / 2. Подробнее см. модифицированный признак Дини.
• Теорема Карлесона: если $f\in L_2([-\pi,\pi])$, то ее ряд Фурье сходится к ней почти всюду. Это верно и если $f\in L_p([-\pi,\pi]), p&amp;amp;gt;1$. Однако, существуют функции из L₁([ − π,π]), ряд Фурье которых расходится во всех точках.
• Зафиксируем точку 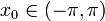$x_0\in(-\pi,\pi)$. Тогда множество всех непрерывных функций, ряд Фурье которых сходится в этой точке, является множеством первой категории в пространстве C([ − π,π]). В некотором смысле это означает, что «типичная» непрерывная функция имеет расходящийся ряд Фурье.

Убывание коэффициентов Фурье и регулярность функции

Существует фундаментальная связь между регулярностью (интегрируемостью, непрерывностью, гладкостью) функции и скоростью убывания ее коэффициентов Фурье. Чем «лучше» функция, тем быстрее ее коэффициенты стремятся к нулю, и наоборот. Степенное убывание коэффициентов Фурье присуще функциям класса C^(k), а экспоненциальное — аналитическим функциям. Примеры такого рода связи:

• Коэффициенты Фурье любой интегрируемой функции стремятся к нулю (Теорема Римана-Лебега).
• Если функция f принадлежит классу C^(k)([ − π,π]), то есть дифференцируема k раз и ее k-я производная непрерывна, то $\hat{f}_n=o\left(\frac{1}{n^k}\right)$
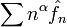• Если ряд $\sum n^{\alpha}\hat{f}_n$ сходится абсолютно, то $f\in C^{(k)}([-\pi,\pi])$ при всех k < α.
• Если функция принадлежит классу Гельдера с показателем α > 1 / 2, то ряд 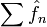$\sum \hat{f}_n$ сходится абсолютно (Теорема Бернштейна).
• Если 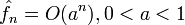$\hat{f}_n=O(a^n),0&amp;amp;lt;a&amp;amp;lt;1$, то функция f является аналитической. Верно и обратное.

См. также

• Преобразование Фурье
• Быстрое преобразование Фурье
• Признак Жордана
• Признак Дини
• Числовой ряд
• АТС теорема

Примечания

Литература

• Жук В.В., Натансон Г.И. Тригонометрические ряды Фурье и элементы теории аппроксимации. — Л.: Изд-во Ленингр. ун-та, 1983. — С. 188.
• Рудин У. Основы математического анализа. — 1976.
• Пискунов Н.С. Дифференциальное и интегральное исчисления для ВТУЗов. — М.: «Наука», 1964. — Т. 2.