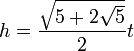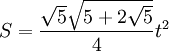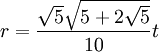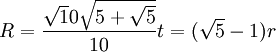Пентагон (фигура)

Правильный пятиугольник

Правильный пятиугольник или пентагон (греч. πενταγωνον) — геометрическая фигура, правильный многоугольник с пятью сторонами.

Свойства

• У правильного пятиугольника угол равен
      $\alpha =\frac{(n - 2)}{n} \cdot 180^\circ = \frac{3}{5} \cdot 180^\circ = 108^\circ$
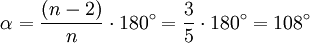
• Площадь правильного пятиугольника с длиной стороны t рассчитывается по формуле:
      $S = \frac{5}{4} t^2 \mathop{\mathrm{ctg}}\, \frac{\pi}{5}$,
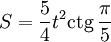  или
  
      $S = \frac{5}{2} R^2 \sin \frac{2 \pi}{5} = 5 r^2 \mathop{\mathrm{tg}}\, \frac{\pi}{5}$,
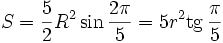  где R — радиус описанной окружности, r — радиус вписанной окружности.
• Отношение диагонали правильного пятиугольника к стороне равно золотому сечению, то есть числу $\frac{1 + \sqrt{5}}{2}$.

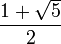Поэтому радиус вписанной окружности, радиус описанной окружности, высоту и площадь правильного пятиугольника можно вычислить и без использования тригонометрических функций:

• Высота правильного пятиугольника:

$h = \frac{\sqrt{5 + 2 \sqrt{5}}}{2} t$

• Площадь правильного пятиугольника:

$S = \frac{\sqrt 5 \sqrt{5 + 2 \sqrt{5}}}{4} t^2$

• Радиус вписанной окружности правильного пятиугольника:

$r = \frac{\sqrt 5 \sqrt{5 + 2 \sqrt{5}}}{10} t$

• Радиус описанной окружности правильного пятиугольника:

$R = \frac{\sqrt 10 \sqrt{5 + \sqrt{5}}}{10} t = ( \sqrt 5 - 1) r$

Построение

Правильный пятиугольник может быть построен с помощью циркуля и линейки, или вписыванием его в заданную окружность, или построением на основе заданной стороны. Этот процесс описан Евклидом в его «Началах» около 300 года до н. э.

Вот один из методов построения правильного пятиугольника в заданной окружности:

1. Постройте окружность, в которую будет вписан пятиугольник и обозначьте её центр как O. (Это зелёная окружность на схеме справа).
2. Выберите на окружности точку A, которая будет одной из вершин пятиугольника. Постройте прямую через O и A.
3. Постройте прямую перпендикулярно прямой OA, проходящую через точку O. Обозначьте одно её пересечение с окружностью как точку B.
4. Постройте точку C посередине между O и B.
5. Проведите окружность с центром в C через точку A. Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D.
6. Проведите окружность с центром в A через точку D. Обозначьте её пересечения с оригинальной (зелёной окружностью) как точки E и F.
7. Проведите окружность с центром в E через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку G.
8. Проведите окружность с центром в F через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку H.
9. Постройте правильный пятиугольник AEGHF.

Альтернативный метод построения правильного многоугольника с помощью линейки и циркуля

Получение с помощью полоски бумаги

Правильный пятиугольник можно получить, завязав узлом полоску бумаги.

Интересные факты

• Додекаэдр — единственный из правильных многогранников, грани которого представляют собой правильные пятиугольники.

Пентагон

• Пентагон — здание Министерства обороны США имеет форму правильного пятиугольника.
• Правильный пятиугольник — правильный многоугольник с наименьшим количеством углов из тех, которыми нельзя замостить плоскость.

См. также

• Золотое сечение
• Пятиугольник
• Пентаэдр
• Пентаграмма
• Государственный Знак Качества СССР

Правильные многоугольники
Треугольник | Четырёхугольник | Пятиугольник | Шестиугольник | Семиугольник | Восьмиугольник | Девятиугольник | Семнадцатиугольник | 257-угольник | 65537-угольник
(См. также: Многоугольник, Теорема Гаусса — Ванцеля)