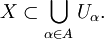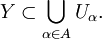Открытое покрытие

Покры́тие в математике — это семейство множеств таких, что их объединение содержит заданное множество. Обычно понятие покрытия рассматривается в контексте общей топологии.

Определения

• Пусть дано множество X. Семейство множеств 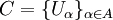$C = \{U_{\alpha}\}_{\alpha \in A}$ называется покрытием X, если

$X \subset \bigcup\limits_{\alpha \in A} U_{\alpha}.$

• Пусть дано топологическое пространство 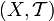$(X,\mathcal{T})$, где X — произвольное множество, а 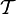$\mathcal{T}$ — определённая на X топология. Тогда семейство открытых множеств 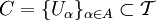$C = \{U_{\alpha}\}_{\alpha \in A} \subset \mathcal{T}$ называется открытым покрытием 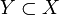$Y \subset X$, если

$Y \subset \bigcup\limits_{\alpha \in A} U_{\alpha}.$

Связанные определения

• Если C — покрытие множества Y, то любое подмножество 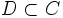$D \subset C$, также являющееся покрытием Y, называется подпокры́тием.
• Если каждый элемент одного покрытия является подмножеством какого либо элемента второго покрытия, то говорят, что первое покрытия впи́сано во второе. Более точно, покрытие 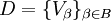$D = \{V_{\beta}\}_{\beta \in B}$ вписано в покрытие 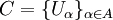$C = \{U_{\alpha}\}_{\alpha \in A}$, если

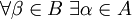$\forall \beta \in B\; \exists \alpha \in A$ такое, что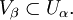 $V_{\beta} \subset U_{\alpha}.$

• Покрытие 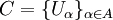$C=\{U_{\alpha}\}_{\alpha \in A}$ множества Y называется лока́льно коне́чным, если для каждой точки 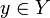$y\in Y$ существует окрестность 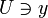$U \ni y$, пересекающаяся лишь с конечным числом элементов C, то есть множество 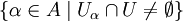$\{\alpha \in A \mid U_{\alpha} \cap U \not= \emptyset \}$ конечно.
• Y называется компактным, если любое его открытое покрытие содержит конечное подпокрытие;
• Y называется паракомпактным, если в любое его открытое покрытие можно вписать локально конечное открытое покрытие.

Свойства

• Любое подпокрытие вписано в изначальное покрытие. Обратное, вообще говоря, неверно.

См. также

• Карта (математика)
• Размерность Лебега