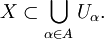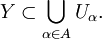Локально конечное покрытие
- Локально конечное покрытие
-
Покры́тие в математике — это семейство множеств таких, что их объединение содержит заданное множество. Обычно понятие покрытия рассматривается в контексте общей топологии.
Определения
- Пусть дано множество X. Семейство множеств
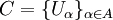 называется покрытием X, если
называется покрытием X, если
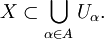
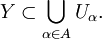
Связанные определения
- Если C — покрытие множества Y, то любое подмножество
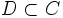 , также являющееся покрытием Y, называется подпокры́тием.
, также являющееся покрытием Y, называется подпокры́тием.
- Если каждый элемент одного покрытия является подмножеством какого либо элемента второго покрытия, то говорят, что первое покрытия впи́сано во второе. Более точно, покрытие
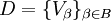 вписано в покрытие
вписано в покрытие 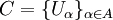 , если
, если
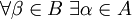 такое, что
такое, что 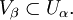
- Покрытие
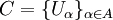 множества Y называется лока́льно коне́чным, если для каждой точки
множества Y называется лока́льно коне́чным, если для каждой точки 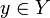 существует окрестность
существует окрестность 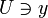 , пересекающаяся лишь с конечным числом элементов C, то есть множество
, пересекающаяся лишь с конечным числом элементов C, то есть множество 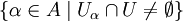 конечно.
конечно.
- Y называется компактным, если любое его открытое покрытие содержит конечное подпокрытие;
- Y называется паракомпактным, если в любое его открытое покрытие можно вписать локально конечное открытое покрытие.
Свойства
- Любое подпокрытие вписано в изначальное покрытие. Обратное, вообще говоря, неверно.
См. также
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое "Локально конечное покрытие" в других словарях:
ЛОКАЛЬНО КОНЕЧНОЕ ПОКРЫТИЕ — покрытиетопологич. пространства его подмножествами такое, что у каждой точки есть окрестность, пересекающаяся лишь с конечным числом элементов этого покрытия. Не из всякого открытого покрытия прямой можно выделить Л. к. п.: достаточно рассмотреть … Математическая энциклопедия
ЛОКАЛЬНО КОНЕЧНОЕ СЕМЕЙСТВО — множеств в топологическом пространстве семейство Fмножеств такое, что у каждой точки пространства есть окрестность, пересекающаяся лишь с конечным множеством элементов семейства F. Важны локально конечные семейства открытых множеств и локально… … Математическая энциклопедия
Покрытие — У этого термина существуют и другие значения, см. Покрытие (значения). Покрытие в математике это семейство множеств, таких, что их объединение содержит заданное множество. Обычно понятие покрытия рассматривается в контексте общей топологии … Википедия
ПОКРЫТИЕ — множества X любое семейство подмножеств этого множества, объединение к рого есть X. 1) Под П. топологического пространства, равномерного пространства и вообще какого либо множества, наделенного тем или иным строением, понимают произвольное П.… … Математическая энциклопедия
Покрытие (математика) — У этого термина существуют и другие значения, см. Покрытие (значения). Покрытие в математике это семейство множеств, таких, что их объединение содержит заданное множество. Обычно понятие покрытия рассматривается в контексте общей топологии … Википедия
Локально стягиваемое пространство — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
Покрытие (в геометрии) — Покрытие в математике это семейство множеств таких, что их объединение содержит заданное множество. Обычно понятие покрытия рассматривается в контексте общей топологии. Содержание 1 Определения 2 Связанные определения 3 Свойства … Википедия
Открытое покрытие — Покрытие в математике это семейство множеств таких, что их объединение содержит заданное множество. Обычно понятие покрытия рассматривается в контексте общей топологии. Содержание 1 Определения 2 Связанные определения 3 Свойства … Википедия
ПАРАКОМПАКТНОЕ ПРОСТРАНСТВО — топологическое пространство, в любое открытое покрытие к рого можно вписать локально конечное открытое покрытие. (Семейство g множеств, лежащих в топологич. пространстве X, наз. локально конечным в X, если у каждой точки существует окрестность в… … Математическая энциклопедия
Топология — (от греч. tоpos место и …логия (См. ...Логия) часть геометрии, посвященная изучению феномена непрерывности (выражающегося, например, в понятии предела). Разнообразие проявлений непрерывности в математике и широкий спектр различных… … Большая советская энциклопедия
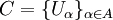 называется покрытием X, если
называется покрытием X, если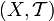 , где X — произвольное множество, а
, где X — произвольное множество, а 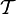 — определённая на X топология. Тогда семейство открытых множеств
— определённая на X топология. Тогда семейство открытых множеств 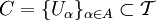 называется открытым покрытием
называется открытым покрытием 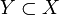 , если
, если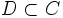 , также являющееся покрытием Y, называется подпокры́тием.
, также являющееся покрытием Y, называется подпокры́тием.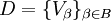 вписано в покрытие
вписано в покрытие 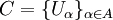 , если
, если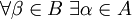 такое, что
такое, что 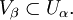
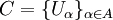 множества Y называется лока́льно коне́чным, если для каждой точки
множества Y называется лока́льно коне́чным, если для каждой точки 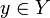 существует окрестность
существует окрестность 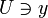 , пересекающаяся лишь с конечным числом элементов C, то есть множество
, пересекающаяся лишь с конечным числом элементов C, то есть множество 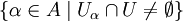 конечно.
конечно.