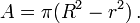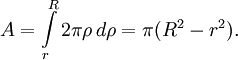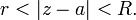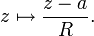Кольцо (геометрическая фигура)

Кольцо

Кольцо — термин в геометрии, используемый для описания похожих на кольцо объектов.

Открытое кольцо является топологическим эквивалентом цилиндра 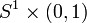$S^1 \times (0,1)$ и проколотой плоскости.

Площадь такого кольца определяется как разность площадей кругов радиусов R и r.

$A = \pi(R^2 - r^2)\,.$

Что интересно, площадь кольца также может быть вычислена путём умножения числа Пи на квадрат половины длины самого большого отрезка, лежащего внутри кольца. Это можно доказать через теорему Пифагора — такой отрезок будет являться касательной к кругу меньшего радиуса. Половина длины отрезка с радиусами r и R образуют прямоугольный треугольник.

Площадь также может быть вычислена путём разбиения кольца на бесконечно малые кольца шириной dρ и площадью 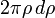$2\pi\rho\, d\rho$ (= окружность × ширину), а затем интегрирования от ρ = r до ρ = R:

$A = \int\limits_r^R 2\pi\rho\, d\rho = \pi(R^2-r^2).$

Комплексная структура

В ТФКП кольцо ann(a; r, R) на комплексной плоскости является открытым множеством и определяется следующим образом:

$r < |z-a| < R.\,$

Если r равно 0, область называется проколотым диском радиуса R вокруг точки a.

Как подмножество комплексной плоскости кольцо может рассматриваться в качестве Римановой поверхности. Комплексная структура кольца зависит только от отношения r/R. Каждое кольцо ann(a; r, R) может быть голоморфно отображено в расположенное в начале координат стандартное кольцо с внешним радиусом 1 с помощью отображения:

$z \mapsto \frac{z-a}{R}.$

Внутренний радиус тогда будет r/R < 1. Теорема Адамара о трёх кругах устанавливает максимальное значение, принимаемое голоморфной функцией внутри кольца.

См. также

• Цилиндр
• Тор (поверхность)

Ссылки

• Площадь кольца, формула, интерактивная анимация (англ.)