Вы можете отметить интересные вам фрагменты текста, которые будут доступны по уникальной ссылке в адресной строке браузера.




Аукционы, объявления, обмен товаров

Тор (поверхность)

Тор (поверхность)
У этого термина существуют и другие значения, см. Тор.
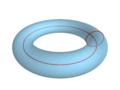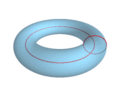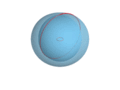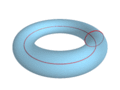
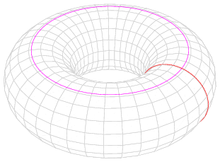Красным - образующая окружность

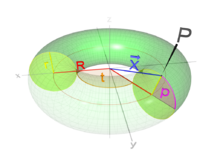
Тор (тороид) — поверхность вращения, получаемая вращением образующей окружности вокруг оси, лежащей в плоскости этой окружности.

  • Открытый тор

  • Двойной тор

  • Triple torus illustration.png

Содержание

Ось тора

Ось тора может лежать вне образующей окружности либо касаться её.

  • Изменение расстояния до оси вращения
  • Standard torus-ring.png
  • Standard torus-horn.png
  • Standard torus-spindle.png
  • Les trois types de tores.PNG

  • анимация

Уравнения

Torus 3d.png
  • Уравнение тора с расстоянием от центра образующей окружности до оси вращения R и с радиусом образующей окружности r может быть задано параметрически в виде:
    \left\{ \begin{matrix} x(\varphi,\psi) = & (R + r \cos \varphi) \cos \psi \\ y(\varphi,\psi) = & (R + r \cos \varphi) \sin \psi \\ z(\varphi,\psi) = & r \sin \varphi \\ \end{matrix} \right. \qquad \varphi, \psi \in [0,2\pi)
  • Непараметрическое уравнение в тех же координатах и с теми же радиусами имеет четвёртую степень:
    \left( x^2+y^2+z^2+R^2-r^2 \right)^2-4R^2\left(x^2+y^2\right)=0
    • В частности, тор является поверхностью четвёртого порядка.
Геометрия на торе, см. Magnetic confinement fusion

Свойства

  • Площадь поверхности тора как следствие из первой теоремы Гульдина: S = 4π2Rr.
  • Объём тела, ограничиваемого тором (полнотория), как следствие из второй теоремы Гульдина: V = 2π2Rr2.
  • Тор с вырезанным диском («проколотый») можно вывернуть наизнанку непрерывным образом (топологически, то есть серией диффеоморфизмов). При этом две пересекающиеся перпендикулярно окружности на нём («параллель» и «меридиан») поменяются местами.[1]

Этапы выворачивания тора

  • Два таких «дырявых» тора, сцепленных между собой, можно продеформировать так, чтобы один из торов «проглотил» другой.[2] Другие парадоксы, связанные с торами можно найти в статьях М. Гарднера, опубликованных в Scientific American в декабре 1972 и декабре 1979 гг.
Гомеоморфность бублика и кружки
Clifford torus
Configuration space

Сечения

  • При сечении тора бикасательной плоскостью, получающаяся кривая четвёртого порядка оказывается вырожденной: пересечение является объединением двух окружностей Вилларсо.
  • Одно из сечений открытого тора - лемниската Бернулли, другие

кривые линии являются графическими линиями и называются кривыми Персея[3] (спирическими линиями, сечениями тора плоскостью, параллельной его оси)

  • Некоторые пересечения поверхности тора плоскостью только внешне напоминают эллипс (кривую 2-го порядка). Получаемая т.о. кривая выражается алгебраическим уравнением 4-го порядка[4].
Сечения

История

Тороидальная поверхность впервые была рассмотрена древнегреческим математиком Архитом при решении задачи об удвоении куба. Другой древнегреческий математик, Персей, написал книгу о спирических линиях — сечениях тора плоскостью, параллельной его оси.

Вариации и обобщения

Тороидальные многогранники

6×4=24 граней

Окрашивание

Минимальное число цветов, необходимое для раскрашивания участков тора так, чтобы соседние были разного цвета, равно 7 (в отличие от 4 для плоскости).

Вариант окраски участков тора

Литература

Савелов А. А. Плоские кривые: Систематика, свойства, применения. М.: Физматгиз, 1960. 293 с. Переиздана в 2002 году, ISBN 5-93972-125-7

См. также

Neo-Riemannian теория

Примечания

  1. ↑ Этапы выворачивания тора были приведены в статье Альберта Такера и Герберта Бейли «Топология» в Scientific American в январе 1950 г.
  2. ↑ Подробности приведены в статьей М. Гарднера в Scientific American за март 1977
  3. ↑ Теоретические основы решения задач по начертательной геометрии: Учебное пособие
  4. ↑ Пересечение сферы и тора плоскостью. Пример построения «линии среза» на поверхности комбинированного тела вращения

Wikimedia Foundation. 2010.

  

См. также в других словарях:

  • Тор — Тор: В Викисловаре есть статья «тор» Тор (поверхность)  геометрическая фигура, поверхность вращения в форме бублика. Тор (мифология)  в скандинавской мифологии один из асов, бог грома и молнии …   Википедия

  • ТОР (в геометрии) — ТОР (от лат. torus выпуклость), геометрическое тело, образуемое вращением круга вокруг непересекающей его и лежащей в одной с ним плоскости прямой. Приблизительную форму тора имеет спасательный круг, баранка. Поверхность, ограничивающую тор,… …   Энциклопедический словарь

  • Тор (геометрич. тело) — Тор (от лат. torus вздутие, выпуклость, узел, валик), геометрическое тело, образуемое вращением круга вокруг прямой, лежащей в плоскости этого круга, но не пересекающей его (см. рис.). Приблизительно форму Т. имеет, например, баранка (или… …   Большая советская энциклопедия

  • тор — (от лат. torus  выпуклость), геометрическое тело, образуемое вращением круга вокруг не пересекающей его и лежащей в одной с ним плоскости прямой. Приблизительно форму тора имеют спасательный круг, баранка. Поверхность, ограничивающую тор, иногда… …   Энциклопедический словарь

  • Тор — I         один из главных богов скандинавской мифологии, бог грома, бури и плодородия (у древних германцев континента ему соответствовал Донар). Т. главный защитник богов и людей от великанов и страшных чудовищ. Изображался рыжебородым богатырём …   Большая советская энциклопедия

  • ТОР — (от лат. torus вздутие, выпуклость, узел) геом. тело, образуемое вращением круга вокруг прямой, лежащей в плоскости этого круга, но не пересекающей его. Приблизительно форму Т. имеет, напр., спасат. круг. Если радиус вращающегося круга равен г… …   Большой энциклопедический политехнический словарь

  • ТОР — (от лат. torus выпуклость), геом. тело, образуемое вращением круга вокруг не пересекающей его и лежащей в одной с ним плоскости прямой. Приблизительно форму Т. имеют спасат. круг, баранка. Поверхность, ограничивающую Т., иногда также наз. Т …   Естествознание. Энциклопедический словарь

  • РИМАНОВА ПОВЕРХНОСТЬ — а н а л и т и ч е с к ой ф у н к ц и и w=f(z) к о м п л е к с н о г о п е р ем е н н о г о z поверхность R такая, что данная полная аналитическая функция w=f(z), вообще говоря многозначная, может рассматриваться как однозначная аналитич. ция… …   Математическая энциклопедия

  • Апплика́тор — (лат. applico, applicatum прикладывать) устройство или приспособление, накладываемое на поверхность тела в качестве источника какого либо вида энергии или носителя вещества, воздействующего на организм …   Медицинская энциклопедия

  • ДЮПЕНА ЦИКЛИДА — поверхность, оба семейства линий кривизны к рой состоят из окружностей, так что она является частным случаем каналовой поверхности. Обе полости эволюты Д. ц. вырождаются в кривые Г 1 и Г 2, являющиеся фокальными кривыми 2 го порядка. Различают Д …   Математическая энциклопедия