Внутренность

У этого термина существуют и другие значения, см. Внутренности.

Окрестность внутренней точки x принадлежит множеству

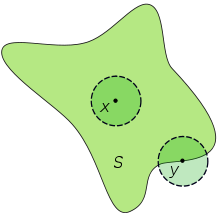
Вну́тренность множества в общей топологии — это совокупность всех внутренних точек. Обычно обозначается Int,^[1] вероятно, от англ. Interior.^{[источник не указан 167 дней]} Иногда внутренность множества называют ядром.^[2]

Определение

Пусть дано топологическое пространство $(X,\mathcal{T}),$ где $X$ — произвольное множество, а $\mathcal{T}$ — определённая на нём топология. Пусть также дано подмножество $A \subset X$. Тогда его внутренностью $A^{0}$ называется совокупность всех внутренних точек $A.$

Свойства

• Операция внутренности является унарной операцией на семействе всех подмножеств $X.$
• Внутренность $A^0$ — открытое множество.
• Внутренность $A^0$ — объединение всех открытых множеств, содержащихся в $A:$

$A^0 = \bigcup\limits_{U \in \mathcal{T},U \subset A} U.$

• Внутренность $A^0$ — наибольшее открытое множество, содержащееся в $A:$

$(U\in \mathcal{T}) \wedge (U\subset A) \Rightarrow (U \subset A^0).$

• Множество $A$ открыто тогда и только тогда, когда оно совпадает со своей внутренностью:

$(A \in \mathcal{T}) \Leftrightarrow \left(A = A^0\right).$

• Операция внутренности идемпотентна:

$\left(A^0\right)^0 = A^0.$

• Операция внутренности сохраняет частичный порядок:

$(A \subset B) \Rightarrow \left( A^0 \subset B^0 \right).$

Примеры

• $\emptyset^0 = \emptyset.$
• Если $A \subset \mathbb{R}^n$ — конечное подмножество евклидова пространства со стандартной топологией, то $A^0 = \emptyset.$
• Если $X = \mathbb{R}$ — вещественная прямая со стандартной топологией, и $[a,b] \subset \mathbb{R},$ то $[a,b]^0 = (a,b).$
• Если $X$ — дискретное пространство, то для любого $A \subset X$ имеем $A = A^0.$

См. также

• Внешность;
• Граница;
• Замыкание.

Примечания

1. ↑ http://www.bodrenko.org/topology/index1,7.html
2. ↑ ВНУТРЕННОСТЬ МНОЖЕСТВА