Теорема Асколи — Арцела

Теорема Асколи — Арцела

Теорема Арцела — утверждение, которое представляет собой критерий предкомпактности множества в полном метрическом пространстве в том специальном случае, когда рассматриваемое пространство — пространство непрерывных функций на отрезке вещественной прямой.

Теорема Арцела — Асколи (или Асколи — Арцела) — это обобщение теоремы Арцела на тот случай, когда рассматриваются семейства отображений метрических компактов (обобщённая теорема Арцела).

Применение теоремы Арцела связано со специальными свойствами рассматриваемых семейств, а именно: с равномерной ограниченностью и равностепенной непрерывностью.

Введение

В математическом анализе (а затем и в функциональном анализе) рассматриваются всевозможные семейства непрерывных функций, заданных на специальных множествах (метрических компактах) и исследуется вопрос о «полноте» таких семейств. В частности, возникает вопрос о существовании предела, например, у последовательности непрерывных числовых функций, заданных на отрезке [a,b], а также о свойствах данного предела. Согласно критерию Коши, равномерный предел непрерывных функций, также является непрерывной функцией, что означает полноту пространства C[a,b]. Существенным здесь является то, что область определения функций — компактное подмножество вещественной прямой (отрезок), а функции принимают значение в полном метрическом пространстве. Аналогичный результат мы получим есть возьмём класс непрерывных отображений произвольного метрического компакта в полное метрическое пространство.

Полнота класса C[a,b] позволяет приблизить всякую непрерывную функцию последовательностью приближений, каждое из которых является функцией в некотором смысле «более простой» чем исходная. Об этом говорит теорема Вейерштрасса: каждую непрерывную функцию на отрезке можно сколь угодно точно приблизить полиномами.

Теорема Арцела относится к тому случаю, когда рассматривается некоторое семейство непрерывных функций 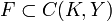$F\subset C(K,Y)$, где K — метрический компакт, а Y — полное метрическое пространство, и исследуется вопрос о том, можно ли выделить из этого семейства сходящуюся подпоследовательность. Поскольку пространство C(K,Y) полное, то существование предельной точки означает, по существу, предкомпактность семейства F в C(K,Y). Поэтому теорему можно сформулировать в общем виде, говоря именно о предкомпактности.

Таким образом, Теорема Арцела представляет собой критерий предкомпактности семейства непрерывных функций, заданных на компакте и действующих в полное метрическое пространство.

Существующий критерий предкомактности множества в полном пространстве требует проверки вполне ограниченности данного множества. На практике, такой критерий не является эффективным. Поэтому представляется целесообразным каким-то образом использовать свойства самих функций, входящих в семейство, чтобы получить критерий прекомпактности, пригодный для применения на практике.

В ходе исследований оказалось, что такими свойствами являются свойства равномерной ограниченности и равностепенной непрерывности рассматриваемого семейства.

Упоминание о равностепенной непрерывности было сделано одновременно Джулио Асколи (ит.)(1883—1884)^[1] и Чезаре Арцела (ит.) (1882—1883)^[2]. Слабая форма теоремы была доказана Асколи в 1883—1884^[1], который установил достаточное условия компактности, и Арцелой в 1895^[3], который привёл необходимое условие и дал первую чёткую интерпретацию результата. Дальнейшее обобщение теоремы было доказано Фреше (1906)^[4] для пространств, в которых понятие предела имеет смысл, например, метрического пространства или хаусдорфового Данфорд, Шварц (1958)^[5]. Современные формулировки теоремы позволяют области и диапазону быть метрическими пространствами. Наиболее общая формулировка теоремы даёт необходимое и достаточное условия для того, чтобы семейство функций из компактного хаусдорфового пространства в Равномерное пространство (англ.) было компактным в топологии равномерной сходимости Бурбаки (1998, § 2.5)^[6].

Определения

Рассмотрим пространство C[a,b] непрерывных функций, заданных на отрезке [a,b], вместе с метрикой равномерной сходимости. Это — полное метрическое пространство. Известно, что:

• Для того, чтобы некоторое подмножество полного метрического пространства было предкомпактным, необходимо и достаточно, чтобы оно было вполне ограниченным.

В случае пространство C[a,b], однако, можно использовать более эффективный критерий предкомпактности, но для этого придётся ввести два следующих ниже понятия.

Положим, что F — некоторое семейство непрерывных функций, заданных на отрезке [a,b].

Равномерная ограниченность

Семейство F называется равномерно ограниченным, если существует единая для всех элементов семейства постоянная K, которой ограничены все функции семейства:

$\forall f\in F\quad\forall x\in[a,b]\quad |f(x)|<K$.

Равностепенная непрерывность

Семейство F называется равностепенно непрерывным, если для любого 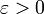$\varepsilon>0$ существует δ > 0 такая, что для всякого элемента 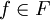$f\in F$ и для любых точек x₁ и x₂ таких, что | x₁ − x₂ | < δ, выполняется строгое неравенство $|f(x_1)-f(x_2)|<\varepsilon$.

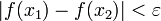Формулировка

Теорема.

Функциональное семейство F является предкомпактным в полном метрическом пространстве C[a,b] тогда и только тогда, когда это семейство является

• равномерно ограниченным и
• равностепенно непрерывным.

Доказательство

Фактически, необходимо показать, что оба указанных свойства семейства функций эквивалентны вполне ограниченности данного семейства.

Необходимость

Итак, пусть семейство F — вполне ограниченное.

Фиксируем 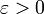$\varepsilon>0$ и построим конечную 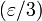$(\varepsilon/3)$-сеть вида: $\{\varphi_i\}_{i=1}^n$.

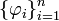Поскольку каждая функция данной системы непрерывна и, следовательно, ограничена, то для каждой такой функции существует своя константа K_i такая что, | f(x) | < K_i для всякого $x\in[a,b]$.

Поскольку таких функций конечное множество, то можно взять $K=\max_{i} K_i+\varepsilon/3$.

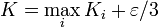Теперь, если взять произвольную функцию 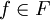$f\in F$, то для этой функции существует такой элемент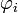 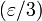$\varphi_i$ $(\varepsilon/3)$-сети, что 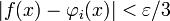$|f(x)-\varphi_i(x)|<\varepsilon/3$ для всякого $x\in[a,b]$. Очевидно, что в этом случае функция f будет ограничена константой K.

Тем самым показано, что семейство F является равномерно ограниченным.

Опять же, в силу непрерывности каждого элемента 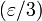$(\varepsilon/3)$-сети, этот элемент оказывается также и равномерно непрерывным и, следовательно, по 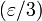$(\varepsilon/3)$ можно подобрать такое δ_i такое, что 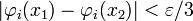$|\varphi_i(x_1)-\varphi_i(x_2)|<\varepsilon/3$ для любых точек $x_1,x_2\in[a,b]$ таких, что | x₁ − x₂ | < δ_i.

Положим δ = min_iδ_i.

Если теперь рассмотреть произвольную функцию 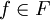$f\in F$, то для заданного 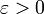$\varepsilon>0$ будет иметь место строгое неравенство 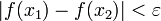$|f(x_1)-f(x_2)|<\varepsilon$ для любых точек $x_1,x_2\in[a,b]$ таких, что | x₁ − x₂ | < δ.

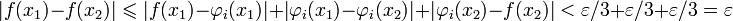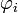Действительно, $|f(x_1)-f(x_2)|\leqslant |f(x_1)-\varphi_i(x_1)|+|\varphi_i(x_1)-\varphi_i(x_2)|+|\varphi_i(x_2)-f(x_2)|<\varepsilon/3+\varepsilon/3+\varepsilon/3=\varepsilon$, где $\varphi_i$ — подходящий элемент 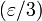$(\varepsilon/3)$-сети.

Тем самым показано, что семейство F является равностепенно непрерывным.

Другими словами, вполнеограниченность влечёт равномерную ограниченность и равностепенную непрерывность.

Достаточность

Теперь необходимо доказать, что равномерная ограниченность и равностепенная непрерывность семейства F влечёт существование конечной $\varepsilon$-сети для всякого конечного $\varepsilon>0$.

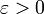Фиксируем $\varepsilon>0$.

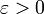Пусть K — это константа, которая фигурирует в определении равномерной ограниченности.

Выберем такое δ > 0, которое фигурирует в определении равномерной непрерывности и соответствует величине $\varepsilon/5$.

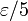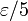Рассмотрим прямоугольник $[a,b]\times[-K,K]$ и разобьём его вертикальными и горизонтальными прямыми на прямоугольные ячейки размером меньше чем δ по горизонтали и $\varepsilon/5$ по вертикали. Пусть x₁, x₂, 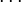$\dots$ , x_N — узлы этой решётки (по оси абсцисс).

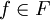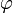Если теперь рассмотреть произвольную функцию $f\in F$, то для каждого узла x_i решётки обязательно найдётся такая точка (x_i,y_j) решётки, что $|f(x_i)-y_j|<\varepsilon/5$. Если теперь рассмотреть ломаную функцию $\varphi$, которая в узлах принимает соответствующие значения, уклоняющиеся от функции не более чем на 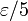$\varepsilon/5$, то в силу того что сама функция уклоняется на каждом отрезке не более чем на 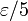$\varepsilon/5$, ломаная на каждом таком отрезке уклоняется не более чем на $3\varepsilon/5$.

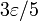Поскольку каждая точка x отрезка [a,b] оказывается на одном из таких отрезков, скажем, [x_k,x_k + 1], то получается что уклонение функции от построенной таким образом ломанной не превосходит $\varepsilon$:

$|f(x)-\varphi(x)|\leqslant|f(x)-f(x_k)|+|f(x_k)-\varphi(x_k)|+|\varphi(x_k)-\varphi(x)| <\varepsilon/5+\varepsilon/5+3\varepsilon/5=\varepsilon$.

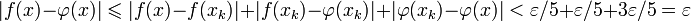Тем самым показано, что конечная (!) система ломанных функций указанного вида является $\varepsilon$-сетью для заданного $\varepsilon>0$.

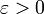Приложения

Теорема Арцела находит своё применение в теории дифференциальных уравнений.

В теореме Пеано (о существовании решения задачи Коши) строится система функций, которая в теории дифференциальных уравнений носит название ломаных Эйлера. Эта система оказывается равномерно ограниченным и равностепенно непрерывным семейством функций, из которого, согласно теореме Арцела можно выделить равномерно сходящуюся последовательность функций, предел которого и будет искомым решением задачи Коши.

См. также

• Лемма Арцела
• Теорема Монтеля о компактном семействе функций — следствие из теоремы Арцела.

Литература

1. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. — изд. третье, переработанное. — М.: Наука, 1972. — 496 с.

Примечания

1. ↑ ^{1 2} Ascoli, G. (1883—1884), «Le curve limiti di una varietà data di curve», Atti della R. Accad. Dei Lincei Memorie della Cl. Sci. Fis. Mat. Nat. 18 (3): 521—586.
2. ↑ Arzelà, Cesare (1882—1883), «Un’osservazione intorno alle serie di funzioni», Rend. Dell' Accad. R. Delle Sci. Dell’Istituto di Bologna: 142—159.
3. ↑ Arzelà, Cesare (1895), «Sulle funzioni di linee», Mem. Accad. Sci. Ist. Bologna Cl. Sci. Fis. Mat. 5 (5): 55-74.
4. ↑ Fréchet, Maurice (1906), «Sur quelques points du calcul fonctionnel», Rend. Circ. Mat. Palermo 22: 1-74, doi:10.1007/BF03018603.
5. ↑ Dunford, Nelson; Schwartz, Jacob T. (1958), Linear operators, volume 1, Wiley-Interscience.
6. ↑ Bourbaki, Nicolas (1998), General topology. Chapters 5-10, Elements of Mathematics, Berlin, New York: Springer-Verlag, MR1726872, ISBN 978-3-540-64563-4.