Процесс Грама ― Шмидта

Процесс Грама (англ.) ― Шмидта — это один из алгоритмов, в которых на основе счётного множества линейно независимых векторов $\mathbf{a}_1,\;\ldots,\;\mathbf{a}_N$ строится множество ортогональных векторов $\mathbf{b}_1,\;\ldots,\;\mathbf{b}_N$ или ортонормированных векторов $\mathbf{e}_1,\;\ldots,\;\mathbf{e}_N$, причём так, что каждый вектор $\mathbf{b}_j$ или $\mathbf{e}_j$ может быть выражен линейной комбинацией векторов $\mathbf{a}_1,\;\ldots,\;\mathbf{a}_j$.

Классический процесс Грама — Шмидта

Алгоритм

Пусть имеются линейно независимые векторы $\mathbf{a}_1,\;\ldots,\;\mathbf{a}_N$.

Определим оператор проекции следующим образом:

$\mathbf{proj}_{\mathbf{b}}\,\mathbf{a} = {\langle \mathbf{a}, \mathbf{b} \rangle \over \langle \mathbf{b}, \mathbf{b}\rangle} \mathbf{b} ,$

где $\langle \mathbf{a}, \mathbf{b} \rangle$ — скалярное произведение векторов $\mathbf{a}$ и $\mathbf{b}$. Этот оператор проецирует вектор $\mathbf{a}$ ортогонально на вектор $\mathbf{b}$.

Классический процесс Грама — Шмидта выполняется следующим образом:

$\begin{array}{lclr} \mathbf{b}_1 & = & \mathbf{a}_1 & (1) \\ \mathbf{b}_2 & = & \mathbf{a}_2-\mathbf{proj}_{\mathbf{b}_1}\,\mathbf{a}_2 & (2) \\ \mathbf{b}_3 & = & \mathbf{a}_3-\mathbf{proj}_{\mathbf{b}_1}\,\mathbf{a}_3-\mathbf{proj}_{\mathbf{b}_2}\,\mathbf{a}_3 & (3) \\ \mathbf{b}_4 & = & \mathbf{a}_4-\mathbf{proj}_{\mathbf{b}_1}\,\mathbf{a}_4-\mathbf{proj}_{\mathbf{b}_2}\,\mathbf{a}_4-\mathbf{proj}_{\mathbf{b}_3}\,\mathbf{a}_4 & (4) \\ & \vdots & & \\ \mathbf{b}_N & = & \mathbf{a}_N-\displaystyle\sum_{j=1}^{N-1}\mathbf{proj}_{\mathbf{b}_j}\,\mathbf{a}_N & (N) \end{array}$

На основе каждого вектора $\mathbf{b}_j \;(j = 1 \ldots N)$ может быть получен нормированный вектор: $\mathbf{e}_j = {\mathbf{b}_j\over \| \mathbf{b}_j \|}$ (у нормированного вектора направление будет таким же, как у исходного, а длина — единичной).

Результаты процесса Грама — Шмидта:

$\mathbf{b}_1,\;\ldots,\;\mathbf{b}_N$ — система ортогональных векторов либо

$\mathbf{e}_1,\;\ldots,\;\mathbf{e}_N$ — система ортонормированных векторов.

Вычисление $\mathbf{b}_1,\;\ldots,\;\mathbf{b}_N$ носит название ортогонализации Грама — Шмидта, а $\mathbf{e}_1,\;\ldots,\;\mathbf{e}_N$ — ортонормализации Грама — Шмидта.

Доказательство

Докажем ортогональность векторов $\mathbf{b}_1,\;\ldots,\;\mathbf{b}_N$.

Для этого вычислим скалярное произведение $\langle \mathbf{b}_1, \mathbf{b}_2 \rangle$, подставив в него формулу (2). Мы получим ноль. Равенство нулю скалярного произведения векторов означает, что эти вектора ортогональны. Затем вычислим скалярное произведение $\langle \mathbf{b}_1, \mathbf{b}_3 \rangle$, используя результат для $\langle \mathbf{b}_1, \mathbf{b}_2 \rangle$ и формулу (3). Мы снова получим ноль, то есть вектора $\mathbf{b}_1$ и $\mathbf{b}_3$ ортогональны. Общее доказательство выполняется методом математической индукции.

Геометрическая интерпретация — вариант 1

Рис. 1. Второй шаг процесса Грама — Шмидта

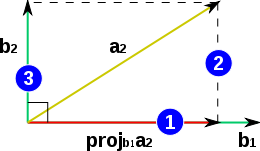
Рассмотрим формулу (2) — второй шаг алгоритма. Её геометрическое представление изображено на рис. 1:

1 — получение проекции вектора $\mathbf{a}_2$ на $\mathbf{b}_1$;

2 — вычисление $\mathbf{a}_2-\mathbf{proj}_{\mathbf{b}_1}\mathbf{a}_2$, то есть перпендикуляра, которым выполняется проецирование конца $\mathbf{a}_2$ на $\mathbf{b}_1$. Этот перпендикуляр — вычисляемый в формуле (2) вектор $\mathbf{b}_2$;

3 — перемещение полученного на шаге 2 вектора $\mathbf{b}_2$ в начало координат. Это перемещение сделано на рисунке лишь для наглядности. Оно не является математическим действием и поэтому не отражается в формуле (2).

На рисунке видно, что вектор $\mathbf{b}_2$ ортогонален вектору $\mathbf{b}_1$, так как $\mathbf{b}_2$ является перпендикуляром, по которому $\mathbf{a}_2$ проецируется на $\mathbf{b}_1$.

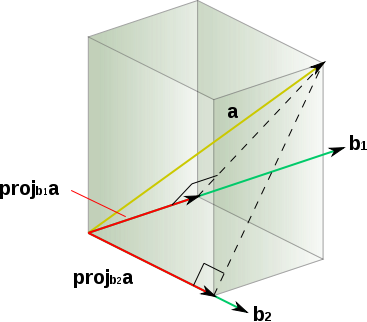
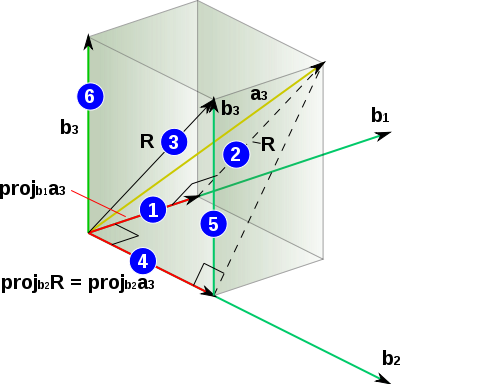
Рассмотрим формулу (3) — третий шаг алгоритма — в следующем варианте:

$\begin{array}{lcr} \mathbf{b}_3 = \mathbf{a}_3-(\mathbf{proj}_{\mathbf{b}_1}\mathbf{a}_3+\mathbf{proj}_{\mathbf{b}_2}\mathbf{a}_3) & & (6) \\ \end{array}$

Её геометрическое представление изображено на рис. 2:

Рис. 2. Третий шаг процесса Грама — Шмидта

1 — получение проекции вектора $\mathbf{a}_3$ на $\mathbf{b}_1$;

2 — получение проекции вектора $\mathbf{a}_3$ на $\mathbf{b}_2$;

3 — вычисление суммы $\mathbf{proj}_{\mathbf{b}_1}\mathbf{a}_3 + \mathbf{proj}_{\mathbf{b}_2}\mathbf{a}_3$, то есть проекции вектора $\mathbf{a}_3$ на плоскость, образуемую векторами $\mathbf{b}_1$ и $\mathbf{b}_2$. Эта плоскость закрашена на рисунке серым цветом;

4 — вычисление $\mathbf{a}_3-(\mathbf{proj}_{\mathbf{b}_1}\mathbf{a}_3 + \mathbf{proj}_{\mathbf{b}_2}\mathbf{a}_3)$, то есть перпендикуляра, которым выполняется проецирование конца $\mathbf{a}_3$ на плоскость, образуемую векторами $\mathbf{b}_1$ и $\mathbf{b}_2$. Этот перпендикуляр — вычисляемый в формуле (6) вектор $\mathbf{b}_3$;

5 — перемещение полученного $\mathbf{b}_3$ в начало координат. Это перемещение сделано на рисунке лишь для наглядности. Оно не является математическим действием и поэтому не отражается в формуле (6).

На рисунке видно, что вектор $\mathbf{b}_3$ ортогонален векторам $\mathbf{b}_1$ и $\mathbf{b}_2$, так как $\mathbf{b}_3$ является перпендикуляром, по которому $\mathbf{a}_3$ проецируется на плоскость, образуемую векторами $\mathbf{b}_1$ и $\mathbf{b}_2$.

Таким образом, в процессе Грама — Шмидта для вычисления $\mathbf{b}_j$ выполняется проецирование $\mathbf{a}_j$ ортогонально на гиперплоскость?, формируемую векторами $\mathbf{b}_1,\;\ldots,\;\mathbf{b}_{j-1}$. Вектор $\mathbf{b}_j$ затем вычисляется как разность между $\mathbf{a}_j$ и его проекцией. То есть $\mathbf{b}_j$ — это перпендикуляр? от конца $\mathbf{a}_j$ к гиперплоскости?, формируемой векторами $\mathbf{b}_1,\;\ldots,\;\mathbf{b}_{j-1}$. Поэтому $\mathbf{b}_j$ ортогонален векторам, образующим эту гиперплоскость?.

Геометрическая интерпретация — вариант 2

Рассмотрим проекции некоторого вектора $\mathbf{a}$ на вектора $\mathbf{b}_1$ и $\mathbf{b}_2$ как компоненты вектора $\mathbf{a}$ в направлениях $\mathbf{b}_1$ и $\mathbf{b}_2$ (рис. 3):

Рис. 3. Вектор $\mathbf{a}$ имеет компоненты в направлениях $\mathbf{b}_1$ и $\mathbf{b}_2$

Если удалить из $\mathbf{a}$ компоненту в направлении $\mathbf{b}_2$, то $\mathbf{a}$ станет ортогонален $\mathbf{b}_2$ (рис. 4):

Рис. 4. Вектор $\mathbf{a}$ имеет компоненту в направлении $\mathbf{b}_1$, а компонента в направлении $\mathbf{b}_2$ отсутствует (нулевая)

Если из $\mathbf{a}$ удалить компоненты в направлениях $\mathbf{b}_1$ и $\mathbf{b}_2$, то $\mathbf{a}$ станет ортогонален и $\mathbf{b}_1$, и $\mathbf{b}_2$ (рис. 5):

Рис. 5. Вектор $\mathbf{a}$ не имеет компонент в направлениях $\mathbf{b}_1$ и $\mathbf{b}_2$

В формуле (2) из вектора $\mathbf{a}_2$ удаляется компонента в направлении вектора $\mathbf{b}_1$. Получаемый вектор $\mathbf{b}_2$ не содержит компоненту в направлении $\mathbf{b}_1$ и поэтому ортогонален вектору $\mathbf{b}_1$.

В формуле (3) из вектора $\mathbf{a}_3$ удаляются компоненты в направлениях $\mathbf{b}_1$ и $\mathbf{b}_2$ (формуле 3 соответствует переход от рис. 3 к рис. 5; рис. 4 не соответствует формуле 3). Получаемый вектор $\mathbf{b}_3$ ортогонален векторам $\mathbf{b}_1$ и $\mathbf{b}_2$.

В формуле (4) из вектора $\mathbf{a}_N$ удаляются компоненты в направлениях $\mathbf{b}_1,\;\ldots,\;\mathbf{b}_{N-1}$. Получаемый вектор $\mathbf{b}_N$ ортогонален векторам $\mathbf{b}_1,\;\ldots,\;\mathbf{b}_{N-1}$.

Таким образом, по формулам (1) — (4) на основе векторов $\mathbf{a}_1,\;\ldots,\;\mathbf{a}_N$ получается набор ортогональных векторов $\mathbf{b}_1,\;\ldots,\;\mathbf{b}_N$.

Численная неустойчивость

При вычислении на ЭВМ по формулам (1) — (5) вектора $\mathbf{b}_1,\;\ldots,\;\mathbf{b}_{N-1}$ часто не точно ортогональны из-за ошибок округления. Из-за потери ортогональности в процессе вычислений классический процесс Грама — Шмидта называют численно неустойчивым.

Модифицированный процесс Грама — Шмидта

Процесс Грама — Шмидта может быть сделан более вычислительно устойчивым путём небольшой модификации. Вместо вычисления $\mathbf{b}_j$ как

$\mathbf{b}_j = \mathbf{a}_j - \mathbf{proj}_{\mathbf{b}_1}\,\mathbf{a}_j - \mathbf{proj}_{\mathbf{b}_2}\,\mathbf{a}_j - \ldots - \mathbf{proj}_{\mathbf{b}_{j-1}}\,\mathbf{a}_j \; (7)$

этот вектор вычисляется следующим образом:

$\begin{array}{lclr} \mathbf{a}_j^{(1)} & = &\mathbf{a}_j - \mathbf{proj}_{\mathbf{b}_1}\,\mathbf{a}_j & (8) \\ \mathbf{a}_j^{(2)} & = &\mathbf{a}_j^{(1)} - \mathbf{proj}_{\mathbf{b}_2} \, \mathbf{a}_j^{(1)} & (9) \\ & \vdots & & \\ \mathbf{a}_j^{(j-2)} & = & \mathbf{a}_j^{(j-3)} - \mathbf{proj}_{\mathbf{b}_{j-2}} \, \mathbf{a}_j^{(j-3)} & (10) \\ \mathbf{b}_j & = & \mathbf{a}_j^{(j-2)} - \mathbf{proj}_{\mathbf{b}_{j-1}} \, \mathbf{a}_j^{(j-2)} & (11) \end{array}$

Геометрическая интерпретация

Рассмотрим получение $\mathbf{b}_3$ по формулам (8) — (11):

$\begin{array}{lllllr} \mathbf{a}_3^{(1)} & = & \mathbf{a}_3 & - & \mathbf{proj}_{\mathbf{b}_1}\,\mathbf{a}_3 & (12) \\ \mathbf{b}_3 & = & \mathbf{a}_3^{(1)} & - & \mathbf{proj}_{\mathbf{b}_2}\,\mathbf{a}_3^{(1)} & (13) \\ \end{array}$

Геометрически это показано на рис 6:

Рис. 6. Геометрическое представление модифицированного процесса

На рис. 6 вектор $\mathbf{a}_3^{(1)}$ обозначен как $\mathbf{R}$.

1 — получение проекции вектора $\mathbf{a}_3$ на $\mathbf{b}_1$ для формулы (12), то есть компоненты $\mathbf{a}_3$ в направлении $\mathbf{b}_1$;

2 — вычитание по формуле (12), то есть удаление из $\mathbf{a}_3$ компоненты в направлении $\mathbf{b}_1$. Получаемый вектор $\mathbf{R}$ ортогонален $\mathbf{b}_1$, так как не имеет компоненты в направлении $\mathbf{b}_1$;

3 — перенос вектора $\mathbf{R}$ в начало координат. Это перемещение сделано на рисунке лишь для наглядности. Оно не является математическим действием и поэтому не отражается в формуле (12).

4 — получение проекции вектора $\mathbf{R}$ на $\mathbf{b}_2$ для формулы (13), то есть компоненты $\mathbf{R}$ в направлении $\mathbf{b}_2$;

5 — вычитание по формуле (13), то есть удаление из $\mathbf{R}$ компоненты в направлении $\mathbf{b}_2$. Получаемый вектор $\mathbf{b}_3$ ортогонален $\mathbf{b}_2$, так как не имеет компоненты в направлении $\mathbf{b}_2$. При вычитании из $\mathbf{R}$ компоненты в направлении $\mathbf{b}_2$ в результирующем векторе $\mathbf{b}_3$ не появляется компонента в направлении $\mathbf{b}_1$;

6 — перенос вектора $\mathbf{b}_3$ в начало координат. Это перемещение сделано на рисунке лишь для наглядности. Оно не является математическим действием и поэтому не отражается в формуле (13).

Таким образом, получаемый на рис. 6 вектор $\mathbf{b}_3$ не имеет компонент в направлениях $\mathbf{b}_1$ и $\mathbf{b}_2$ и поэтому ортогонален $\mathbf{b}_1$ и $\mathbf{b}_2$.

Рассмотрим непосредственно формулы (8) — (11).

В формуле (8) из вектора $\mathbf{a}_j$ удаляется компонента в направлении вектора $\mathbf{b}_1$. Получаемый вектор $\mathbf{a}_j^{(1)}$ не содержит компоненту в направлении $\mathbf{b}_1$ и поэтому ортогонален вектору $\mathbf{b}_1$.

Далее в формуле (9) из результата удаляется его компонента в направлении вектора $\mathbf{b}_2$. Получаемый вектор $\mathbf{a}_j^{(2)}$ не содержит компоненту в направлении $\mathbf{b}_2$ и поэтому ортогонален вектору $\mathbf{b}_1$.

Путём дальнейшего последовательного удаления из результата его компонент получается вектор $\mathbf{b}_j$, не содержащий компонент в направлениях $\mathbf{b}_1,\;\ldots,\;\mathbf{b}_{j-1}$ и потому ортогональный векторам $\mathbf{b}_1,\;\ldots,\;\mathbf{b}_{j-1}$.

Эквивалентность классического и модифицированного процессов

Классический и модифицированный процессы можно сопоставить следующим образом:

$\begin{array}{l} \mathbf{b}_j\\ \\ \mathbf{b}_j \end{array} \begin{array}{c} = \\ \\ = \end{array} \underbrace{ \underbrace{ \underbrace{ \begin{array}{c} \mathbf{a}_j \\ \\ \mathbf{a}_j \end{array} \begin{array}{c} - \\ \\ - \end{array} \begin{array}{c} \mathbf{proj}_{\mathbf{b}_1}\,\mathbf{a}_j \\ || \\ \mathbf{proj}_{\mathbf{b}_1}\,\mathbf{a}_j \end{array} }_{\mathbf{a}_j^{(1)}} \begin{array}{c} - \\ \\ - \end{array} \begin{array}{c} \mathbf{proj}_{\mathbf{b}_2}\,\mathbf{a}_j \\ || \\ \mathbf{proj}_{\mathbf{b}_2}\,\mathbf{a}_j^{(1)} \end{array} }_{\mathbf{a}_j^{(2)}} \begin{array}{c} - \\ \\ - \end{array} \begin{array}{c} \mathbf{proj}_{\mathbf{b}_3}\,\mathbf{a}_j \\ || \\ \mathbf{proj}_{\mathbf{b}_3}\,\mathbf{a}_j^{(2)} \end{array} }_{\mathbf{a}_j^{(3)}} \begin{array}{ccc} - & \ldots & - \\ \\ - & \ldots & - \end{array} \begin{array}{cc} \mathbf{proj}_{\mathbf{b}_{j-1}}\,\mathbf{a}_j & (14) \\ || & \\ \mathbf{proj}_{\mathbf{b}_{j-1}}\,\mathbf{a}_j^{(j-2)} & (15) \end{array}$

Формула (14) показывает вычисление $\mathbf{b}_j$ в классическом процессе, а формула (15) — в модифицированном.

Разница между (14) и (15) заключается в том, от каких векторов вычисляются компоненты: от $\mathbf{a}_j$ в классическом процессе или от результата предыдущего вычитания, то есть от $\mathbf{a}_j^{(k)}$ в модифицированном процессе. $\mathbf{a}_j^{(k)}$ представляет собой $\mathbf{a}_j$, из которого удалены компоненты в направлениях $\mathbf{b}_1,\,\;\ldots,\;\mathbf{b}_{k}$. Компонента вектора $\mathbf{a}_j$ в направлении $\mathbf{b}_{k+1}$ при этом удалении не затрагивается и поэтому она в $\mathbf{a}_j^{(k)}$ такая же, как в $\mathbf{a}_j$. Другими словами,

$\mathbf{proj}_{\mathbf{b}_{k+1}}\,\mathbf{a}_j^{(k)} = \mathbf{proj}_{\mathbf{b}_{k+1}}\,\mathbf{a}_j (16)$

На рис. 6 равенство (16) имеет форму «$\mathbf{proj}_{\mathbf{b}_2}\,\mathbf{R} = \mathbf{proj}_{\mathbf{b}_2}\,\mathbf{a}_3$».

Равенство (16) отображено знаками "||" между формулами (14) и (15). Это позволяет видеть, что формулы (14) и (15) эквивалентны. Таким образом, классический и модифицированный процессы эквивалентны, но только при идеально точных вычислениях. Реальные вычисления имеют погрешность из-за ошибок округления.

Особые случаи

Процесс Грама — Шмидта может применяться также к бесконечной последовательности линейно независимых векторов.

Кроме того, процесс Грама — Шмидта может применяться к линейно зависимым векторам. В этом случае он выдаёт $\mathbf{0}$ (нулевой вектор) на шаге $j$, если $\mathbf{a}_j$ является линейной комбинацией векторов $\mathbf{a}_1,\;\ldots,\;\mathbf{a}_{j-1}$. Если это может случиться, то для сохранения ортогональности выходных векторов и для предотвращения деления на ноль при ортонормировании алгоритм должен делать проверку на нулевые вектора и отбрасывать их. Количество векторов, выдаваемых алгоритмом, будет равно размерности подпространства, порождённого векторами (т.е. количеству линейно независимых векторов, которые можно выделить среди исходных векторов).

Свойства

• Матрица перехода от $\mathbf{a}_1,\;\ldots,\;\mathbf{a}_j$ к $\mathbf{b}_1,\;\ldots,\;\mathbf{b}_j$ — верхнетреугольная матрица.

• Произведение длин $\mathbf{b}_1,\;\ldots,\;\mathbf{b}_j$ равно объёму параллелепипеда, построенного на векторах системы $\mathbf{a}_1,\;\ldots,\;\mathbf{a}_j$ как на рёбрах.

Единственность результата

Матрица перехода от $\mathbf{a}_1,\;\ldots,\;\mathbf{a}_j$ к $\mathbf{e}_1,\;\ldots,\;\mathbf{e}_j$ и множество векторов $\mathbf{e}_1,\;\ldots,\;\mathbf{e}_j$ определяются однозначно, если принять, что диагональные элементы матрицы перехода положительны.

Дополнительные толкования

Процесс Грама ― Шмидта может быть истолкован как разложение невырожденной квадратной матрицы в произведение ортогональной (или унитарной матрицы в случае эрмитова пространства) и верхнетреугольной матрицы с положительными диагональными элементами ― QR-разложение, что есть частный случай разложения Ивасавы.

Реализации

Реализация для пакета Mathematica

Данный скрипт, предназначенный для пакета Mathematica, проводит процесс ортогонализации Грама ― Шмидта над векторами, заданными в фигурных скобках предпоследней строки. Количество векторов и их координат могут быть произвольными. В данном случае для примера взяты векторы $\{-2,\;1,\;0\}$, $\{-2,\;0,\;1\}$, $\{-0{.}5,\;-1,\;1\}$.

Projection[v1_, v2_] := (v1.v2*v2)/v2.v2
MultipleProjection[v1_, vecs_] := Plus @@ (Projection[v1, #1] &) /@ vecs
GramSchmidt[mat_] := Fold[Join[#1, {#2 - MultipleProjection[#2, #1]}] &, {}, mat]
GramSchmidt[{{-2, 1, 0}, {-2, 0, 1}, {-0.5, -1, 1}}]

Литература

• Беклемишев Д. В. Курс аналитической геометрии и линейной алгебры. — М.: Наука.