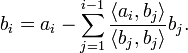Ортогонализация Грама ― Шмидта

Процесс Грама ― Шмидта ― наиболее известный алгоритм ортогонализации, при котором по линейно независимой системе 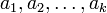$a_1, a_2,\dots,a_k$ строится ортогональная система 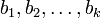$b_1, b_2,\dots,b_k$ такая, что каждый вектор b_i линейно выражается через 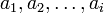$a_1,a_2,\dots,a_i$, то есть матрица перехода от {a_i} к {b_i} ― верхнетреугольная матрица. При этом можно добиться того, чтобы система {b_i} была ортонормированной и чтобы диагональные элементы матрицы перехода были положительны; этими условиями система {b_i} и матрица перехода определяются однозначно.

Этот процесс применим также и к счётной системе векторов.

Процесс Грама ― Шмидта может быть истолкован как разложение невырожденной квадратной матрицы в произведение ортогональной (или унитарной матрицы в случае эрмитова пространства) и верхнетреугольной матрицы с положительными диагональными элементами, что есть частный случай разложения Ивасавы.

Алгоритм

Полагают b₁ = a₁, и, если уже построены векторы 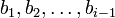$b_1,b_2,\dots,b_{i-1}$, то

$b_i=a_i-\sum_{j=1}^{i-1}\frac{\langle a_i,b_j\rangle}{\langle b_j,b_j\rangle} b_j.$

Геометрический смысл описанного процесса состоит в том, что на каждом шагу вектор b_i является перпендикуляром, восстановленным к линейной оболочке векторов 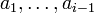$a_1,\dots,a_{i-1}$ до конца вектора a_i.

Нормируя полученные векторы b_i,

c_i = b_i / | b_i |

получают искомую ортонормированную систему {c_i}.

Реализация алгоритма

Данный скрипт, предназначенный для пакета { − 2,1,0}, { − 2,0,1}, { − 0.5, − 1,1}

Projection[v1_, v2_] := (v1.v2*v2)/v2.v2
MultipleProjection[v1_, vecs_] := Plus @@ (Projection[v1, #1] &) /@ vecs
GramSchmidt[mat_] := Fold[Join[#1, {#2 - MultipleProjection[#2, #1]}] &, {}, mat]
GramSchmidt[{{-2, 1, 0}, {-2, 0, 1}, {-0.5, -1, 1}}]
Null

Свойства

• Произведение длин b_i равно объёму параллелепипеда, построенного на векторах системы {a_i}, как на рёбрах.